The 15 Best Math Tricks for Kids
Make mental math a breeze with these quick and easy math tricks.

Author
Jill Padfield
Published:
Nov 2024
Key takeaways
- Math is full of tricks and shortcuts – Because math is so interwoven and connected, you can find plenty of ways to tackle new problems by using skills you already have.
- You can save lots of time – By remembering just a few of these tricks, you can dramatically cut down on mental math.
- Take a peek behind the curtain – Learning the logic behind some of these tricks can reveal fundamental math principles.
Whether going about your daily routine or practicing math problems after your latest lesson, you will likely use math every single day. And while this practice can be fun and rewarding on its own, sometimes you need to cut down on time or simply knock out basic math problems on the way to something more complex.
Fortunately, there are plenty of math tricks you can learn to save you time and frustration. Memorizing a few of these will make your adventures through math much smoother, and they may even help you and your learner understand more complex concepts down the line.
Table of contents
Access more math practice with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Addition tricks
Addition can appear not too challenging on its own, but adding large numbers or finding large sums can be time-consuming. Here are a few tricks to make addition much quicker.
1. Break numbers down
People struggle with addition when the numbers are not all nice and even. For example, adding 73 and 19 together might take even the quickest math mind a second to calculate. For young learners in particular, this can become overwhelming and discouraging.
To make this kind of addition easier, break the numbers down into more manageable chunks.
Let’s use the example above: 73 + 19.
First, take both numbers and break them up.
73 = 70 + 3
19 = 10 + 9
With this approach, you have numbers that are much easier to add.
70 + 10 = 80
3 + 9 = 12
Now, add the two sums together:
80 + 12 = 92
You have your answer, and it was much easier to do in your head.
2. Round numbers up
Another way to take complex numbers and find their sum easily is to round them up to the nearest number ending in zero. For instance, if you wanted to add 347 and 559 together, that might take a second. Instead, try rounding.
First, round each number up to the nearest tenth place:
347 becomes 350
559 becomes 560
Now, you have 350 and 560, which are easier to add together:
350 + 560 = 910
Next, look at how much you rounded each number up and add the total together:
350 – 347 = 3
560 – 559 = 1
3 + 1 = 4
Then, subtract that total from 910:
910 – 4 = 906
That means 347 + 559 = 906.
Subtraction tricks
Subtraction has a few tricks that are similar that will make your daily mental math a breeze.
3. Use a little addition
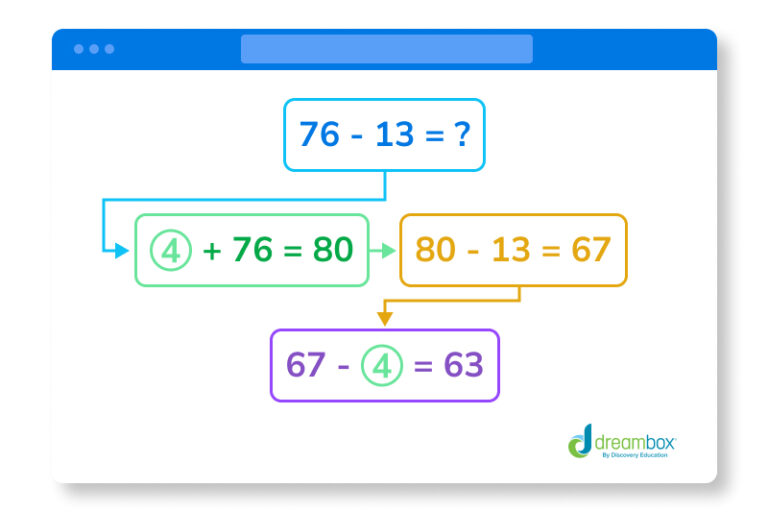
To quickly subtract two numbers, you can add enough to one number to make it a multiple of 10 and then subtract. You will then subtract what you added from that number to get your final answer.
For example, what is 76 – 13 = ?
First, add 4 to 76 to get 80, which is easier to work with.
Now rewrite the problem using 80:
80 – 13 = ?
Subtract 13 from 80:
80 – 13 = 67
Subtract the 4 you added earlier, and you have your answer:
67 – 4 = 63
Therefore, 76 – 13 = 63.
4. Remember your multiplication tables
This trick can work for addition as well. If you have a problem where the number you are subtracting from is a multiple of the number you are subtracting, you can simply think back to the multiplication table.
For example, if you have 81 – 9, you know that 81 is a multiple of 9: 9 x 9 to be exact. That means if you subtract 9 from 81, you are looking for the product of 9 x 8, which is 72.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Multiplication tricks
Depending on the numbers you are multiplying, you will find lots of tricks at your disposal to make multiplication much easier to do in your head.
5. Multiply large numbers
One way to handle any larger numbers in multiplication is to use their distance from 100. This will work for any two digit numbers.
Consider the problem, 91 x 97.
The first step is to subtract each number from 100.
100 – 91 = 9
100 – 97 = 3
Now, find the sum of those two results:
9 + 3 = 12
Next, subtract that from 100:
100 – 12 = 88
This gives you the first portion of your answer, in the hundreds. So here, you have 8,800.
Now, you multiply the two numbers you got before from the difference from 100:
9 x 3 = 27
Add the product to the first part of your answer:
8,800 + 27 = 8,827
Therefore, 91 x 97 = 8,827.
This works best with double digits numbers that are close to 100, preferably in the 90s, so the addition at the end is easy.
6. The rule of 6s
Whenever you multiply an even number by 6, you can find the ones place of the product very easily. The rule of 6 is that the ones place of the product will always match the ones place of the number you are multiplying by 6.
For example, look at 6 x 14. Thanks to this rule, we know the answer will have a 4 in the ones place.
6 x 14 = 84
As you can see, 14 and 84 both have a 4 in the ones place.
7. The rule of 5s with even numbers
You probably already know that all multiples of 5 end in either 5 or 0, but this trick will make finding these multiples even easier.
For any even number you are multiplying by 5, divide it by 2. Add a zero to that number, and you have your answer. Check out 5 x 8.
Half of 8 is 4, and now you can just add a 0 after the 4 to get your answer.
5 x 8 = 40.
8. The rule of 5s with odd numbers
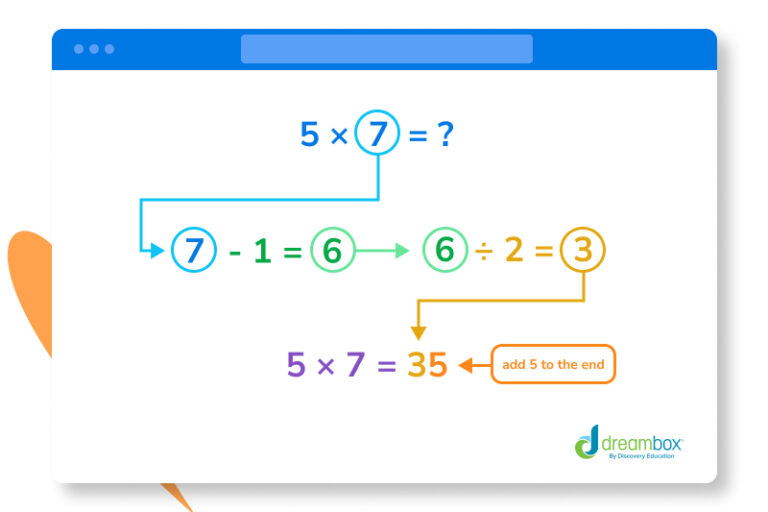
Multiplying 5 by odd numbers is just a little bit tricker, but this math tip still makes the multiplication a breeze.
Say you want to find the product of 5 x 7. The first step is to subtract 1 from the odd number you are multiplying by 5. That means 7 becomes 6.
After that, just like before, divide this number (6) by 2. This will get 3.
Now, add a 5 after the 3 to get 35. This is your answer.
5 x 7 = 35
9. The rule of 9s
If you are trying to remember the multiples of 9, this trick is invaluable. If a number is a multiple of 9, the sum of the individual digits will always equal 9.
For example, 9 x 2 = 18, and 1 + 8 = 9.
Let’s try it with some larger numbers. 9 X 1,223 = 11,007, and 1 + 1 + 0 + 0 + 7 = 9.
If you’re ever unsure about your work, you can use this trick to check your answer.
10. Use your fingers
Adding with your fingers is easy, but did you know you can use those digits to multiply, too? This handy trick allows you to easily figure out multiples of 9. Let’s try this with 9 x 6.
Start with both hands palms out in front of you, all fingers and thumbs extended. For any number you are multiplying by 9 (which is 6 for this example) start counting fingers from the very most left finger. Once you get to 6, put that finger down. For 6, that would be the thumb on your right hand. You should have five fingers up on your left hand and 4 on your right.
To figure out the answer to 9 X 6 from this, look at the number of fingers on both sides of the finger you put down. You have 5 on the left, and 4 on the right. That means your answer is 54.
11. Multiply any two-digit number by 11
Multiplying any one-digit number by 11 is a simple trick most people already know: you just duplicate the number!
4 x 11 = 44
7 x 11 = 77
That’s nice and easy. However, multiplying two-digit numbers by 11 can be a little trickier, but it’s still easy with this technique.
All you need to do is add up the two numbers of the multiplicand and place the sum in between the two numbers.
For instance, take 34 x 11.
First, sum the two digits of the multiplicand (34):
3 + 4 = 7
Next, place the sum in between the two digits you multiplied:
Place 7 in between 3 and 4 to get 374
Therefore, 34 x 11 = 374.
If the sum of the first and second digit is greater than 9, still put the sum in the tens place, but add the tens portion to the hundredths place.
For example, 11 x 76 = 836.
The way we got here was by adding the two digits of the multiplicand:
7 + 6 = 13
Since 13 > 9, if you place the 13 in the middle of 7 and 6 you would get 7,136. Instead, add the 7 and 1 together in the hundredths place to get 836.
Division tricks
Division can be tricky, but, with a few tricks of your own, you can make some basic division completely worry-free.
12. The digits reveal a lot
You can easily determine if a number is divisible by certain other numbers just by looking at the last digit or by doing some simple addition.
- All numbers ending in 0 are divisible by 10.
- All numbers where the digits add up to 9 are divisible by 9.
- All numbers where the last three digits are evenly divisible by 8 (or are 000) are divisible by 8.
- All numbers that are even, and have digits that add up to a number that’s divisible by 3, are divisible by 6.
- All numbers ending in 0 or 5 are divisible by 5.
- All numbers where the last two digits form a number that’s divisible by 4 are also divisible by 4. This is also true for numbers that end with 00.
- All numbers where the digits add up to a number divisible by 3 are divisible by 3.
- And all numbers that are divisible by 2 will end in 0, 2, 4, 6, or 8.
Other math tricks
Division can be tricky, but, with a few tricks of your own, you can make some basic division completely worry-free.
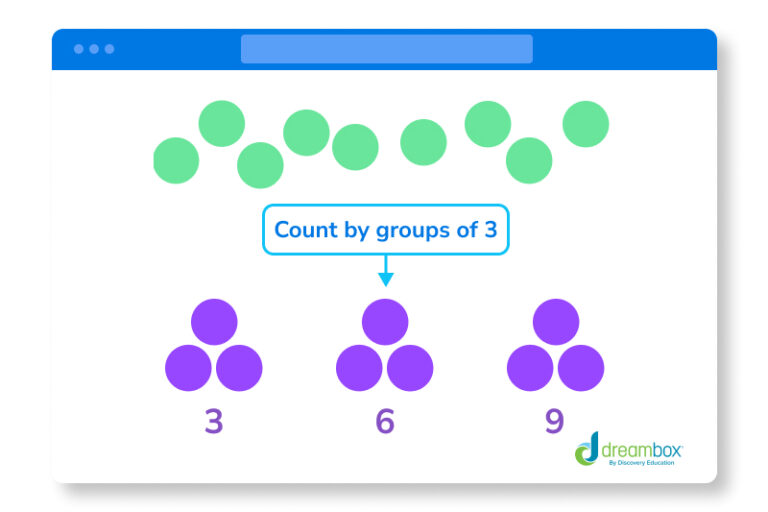
13. Quicker counting
If you have a large quantity of things to count, like pieces of Halloween candy, counting each individual Snickers bar will take a while. Instead, if you count by groups of 2 or 3, you can count much quicker.
Instead of counting 1, 2, 3, and so on, you can count 3, 6, 9 until you are done. This is much faster and also helps you practice with multiples.
14. Quicker counting
You can blow some minds by showing how you can get 1,089 as an answer for some simple math problems with any three-digit number.
The first step is to take any three-digit number and rearrange the digits into descending and ascending order. For example, take the number 724:
Descending order: 742
Ascending order: 247
Now, subtract the ascending version from the descending version:
742 – 247 = 495
After you have this number, reverse it:
495 reversed is 594
Then, add these two numbers up:
495 + 594 = 1,089
No matter what three-digit number you use for this trick, you will always end up with 1,089.
15. Quickly compare fractions
If you are trying to figure out which of two fractions is the largest one, you can do some quick multiplication to get your answer.
For example, which is larger, 7⁄9 or 8⁄11?
First, you multiply the numerator of the first number by the denominator of the second:
7 x 11 = 77
Now, you multiply the denominator of the first number by the numerator of the second number:
9 x 8 = 72
If the first product is larger, the first fraction is the largest, and if the second product is the biggest, then the second fraction is the largest.
77 > 72
This means 7⁄9 is greater than 8⁄11.
FAQs about math tricks for kids
Some popular tricks include the “Finger Trick,” where using fingers helps quickly determine multiples of nine. Additionally, teaching learners the “Counting by Multiples Trick” allows them to count larger quantities easily while teaching multiples. These tricks not only boost mathematical abilities, but they also instill confidence in young learners.
1. If there are 4 apples and you take away 3, how many apples do you have?
(Answer: You have 3)
2. Which number stays the same no matter how many times you multiply it?
(Answer: 0)
3. I am more than 10 but less than 15. I am one more than the number of months in a year. What am I?
(Answer: 13)
4. Fill in the blanks; 4, 8, 12, _, 20, _, 28
(Answers: 16 and 24)
Mastering these shortcuts can improve problem-solving skills, which helps with math assignments and real-world challenges. In everyday life, these tricks can help kids quickly calculate tips at restaurants, mentally estimate costs while shopping, or figure out time-related problems effortlessly.
For elementary school students, simple math tricks work best. Learning about patterns in multiples of 10 or 5 is an easy start, and the “rule of 9s” trick can make that part of learning multiplication much easier.
You can introduce math tricks through interactive games, puzzles, demonstrations, and activities. For instance, organizing a “Math Magic Show” where kids perform tricks for each other fosters a collaborative and engaging learning environment, while making math fun.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


