What Is the Associative Property of Addition?
No matter which order you put things in, you’ll always get the same answer – at least when it comes to addition!

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- No matter how you write an equation, the sum remains the same – That’s the basic breakdown of the associative property of addition!
- Grouping can help us simplify equations – Grouping numbers together helps us break up an equation and more easily calculate the sum.
- The associative property applies to multiplication, too – You can group factors together and, no matter how you combine the groups, you always get the same product.
There are a lot of rules in math. Sometimes, this can make the subject seem dry or boring, but actually, these rules are meant to help make things a little easier!
Think of the associative property as a rule of addition. To “associate” means to connect or join with something else. In addition, we’re connecting different numbers together to create a sum.
The associative property tells us that no matter how we arrange three or more numbers in an equation, we’ll always get the same sum. But how and why? Let’s take a closer look.
What is the associative property of addition?
The associative property of addition states that the sum of three or more numbers will always remain the same, regardless of how the numbers are grouped. But what is grouping, and how does it work? Let’s break it down.
Grouping
Grouping is the practice of bringing two or more terms together into a group.
In an equation, we usually represent grouping by using parentheses.
For example, let’s say we have the equation:
4 + 5 + 6 + 7 = 22
We can use grouping to make this equation a little easier to read. All we have to do is group two terms together. In this case, we could group the first two terms together and the last two terms together.
So now the equation looks like this:
(4 + 5) + (6 + 7) = 22
If we solve the parentheses to simplify the equation, we get:
9 + 13 = 22
The associative property of addition
Put simply, whenever you add multiple numbers together, you can group them any way that you like and still end up with the same answer. That’s because you still have the same quantity, regardless of how you write the equation.
Let’s take a look at what this means visually:
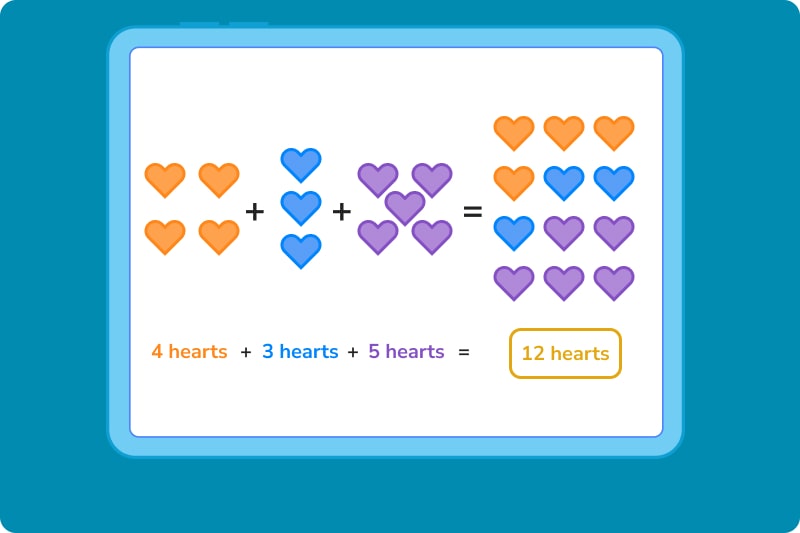
Even if we switch the order of things, the number of hearts remains the same.
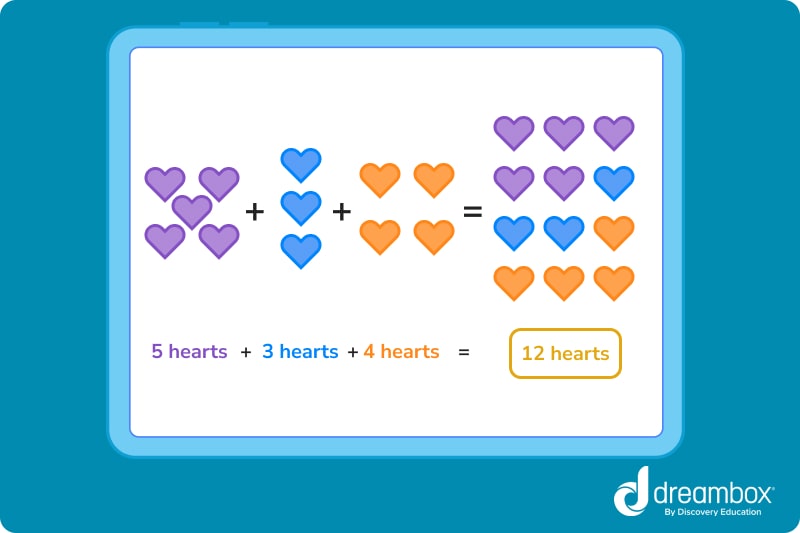
Table of contents
Access more math practice with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Grouped equations
Let’s look at how you can write equations a few different ways and, using the associative property of addition, still get the same result.
Let’s examine this equation:
6 + 8 + 10 + 12 = 36
Now, we’re going to use grouping and see if we can make that 36 number change (spoilers: we can’t!).
First, let’s make it simple and just group the numbers as they’re written.
(6 + 8) + (10 + 12) = 36
We’ll solve the addition problems in the parentheses and get:
14 + 22 = 36
Okay, what if we swap the numbers on the end?
12 + 8 + 10 + 6 = 36
And put them into parentheses?
(12 + 8) + (10 + 6)
We’ll solve the addition problems in the parentheses and guess what?
20 + 16 = 36
And on and on it goes!
What about the commutative property of addition?
Think about the word “commute.” It means to move, right? The commutative property of addition says that we can rearrange the order of numbers and still get the same result.
In other words, the commutative property helps make the associative property true.
To put it into an equation:
A + B = B + A
Or, if you decide to rearrange it:
B + A = A + B
Neat, right?!
Where else does the associative property apply?
The associative property also applies to multiplication! So, let’s take a look at a multiplication problem.
Say you have:
4 × 6 × 7 × 4 = 672
If we group those in order, we get:
(4 × 6) × (7 × 4) = 672
4 × 6 = 24
7 × 4 = 28
And that becomes:
24 × 28 = 672
Now, let’s swap some things around:
7 × 6 × 4 × 4 = 672
Grouped, that looks like:
(7×6) × (4×4) = 672
7×6 = 42
4×4 = 16
And that becomes:
42 × 16 = 672
Using the associative property makes finding the sum (or the product!) easier when you have multi-digit numbers to add together. Just keep this rule in mind as you dive into your math homework, and you can conquer those problems with ease!

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Let’s practice together
1. Find the sum: (5 + 6) + (7 + 8)
So, since these are grouped together, we can break this up into parts to find the sum.
First, we’ll add the numbers in parentheses together:
5 + 6 = 11
7 + 8 = 15
Then, add these larger sums together:
11 + 15 = 26
2. Find the sum: (7 + 5) + (6 + 8)
Instead of going through the long process of solving, look at the answer above. Using the associative property of addition, we know that the sum is 26.
Ready to give it a go?
- Now that you’ve learned all about the associative property of addition, it’s your turn to shine! Solve the following problems to test your knowledge and understanding.
Practice Problems
Click to reveal the answer.
The answer is 40
The answer is 30
The answer is YES
The answer is 5,184
Parent Guide
- 1. The answer is 40. How did we get here? If you add all of these numbers together, you get 40.
- 2. The answer is TRUE. How did we get here? Using the associative property, we know that you can group the numbers in a different order and still get the same sum.
-
3. The answer is 30. How did we get here?
- First, we solve the equations in parentheses.
- 6 + 3 = 9
- 14 + 7 = 21
- Then, we add those two numbers together to get our answer:
- 9 + 21 = 30
- First, we solve the equations in parentheses.
- 4. The answer is YES. How did we get here? Using the associative property of addition, we know that no matter what order the numbers are in, if they are the same numbers, they will produce the same sum.
-
5. The answer is 5,184. How did we get here?
- Multiply 9 by 9 to get 81.
- Multiply 8 by 8 to get 64.
- Then multiply 81 by 64 to get 5,184.
FAQs about math strategies for kids
According to the associative property, while adding or multiplying numbers, the way in which the numbers are grouped by brackets does not affect their sum or product.
You can shuffle the numbers however you like within the equation, but the answer will always remain the same.
The associative property states you can group different numbers in various ways without changing the outcome. The commutative property states you can reorder the numbers without changing the outcome.
No, it does not. The order of operations in subtraction helps determine whether a number is positive or negative, and also drastically changes the outcome. So, for example:
5 – 6 – 8 = -9
8 – 6 – 5 = -3
That means that 5 – 6 – 8 ≠ 8 – 6 – 5
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


