How to Convert Decimals to Fractions

By the end of this lesson you will feel more confident converting decimals to fractions making you more prepared for other fifth-grade math lessons!

Author
Amber Watkins

Published
November 7, 2023

How to Convert Decimals to Fractions

By the end of this lesson you will feel more confident converting decimals to fractions making you more prepared for other fifth-grade math lessons!

Author
Amber Watkins

Published
Nov 7, 2023

How to Convert Decimals to Fractions

By the end of this lesson you will feel more confident converting decimals to fractions making you more prepared for other fifth-grade math lessons!

Author
Amber Watkins

Published
Nov 7, 2023

Key takeaways

Knowing how to convert a decimal to fraction equivalents is a required skill learned in fifth-grade math.
Converting decimals to fractions doesn’t change the value of the decimals, it simply allows us to use it in other ways.
Converting decimals to fractions requires a good understanding of place values and a general knowledge of finding the GCF (Greatest Common Factor) in order to simplify them.

Table of contents

Converting decimals to fractions doesn’t have to be intimidating. If you can read a decimal, you can change that decimal into a fraction.

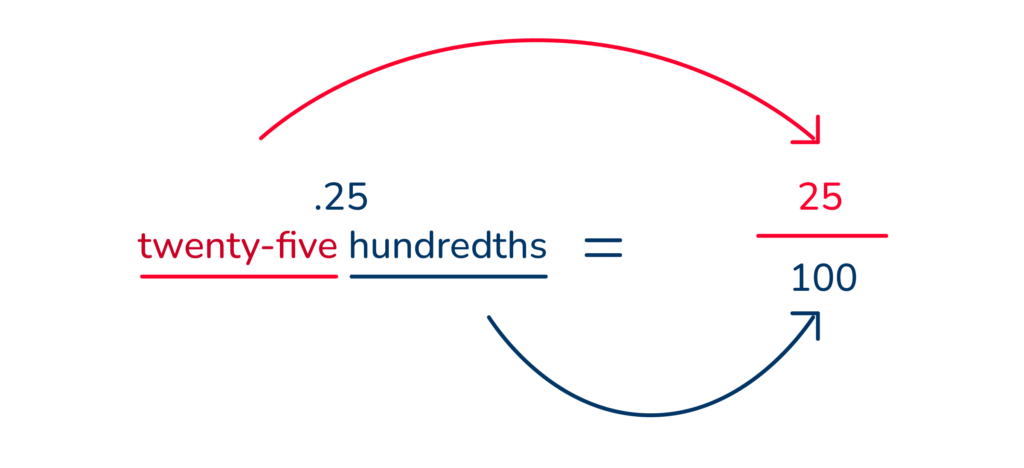
When you read .25 you say “twenty-five hundredths”. The number 25 is placed on the top of the fraction and 100 on the bottom.

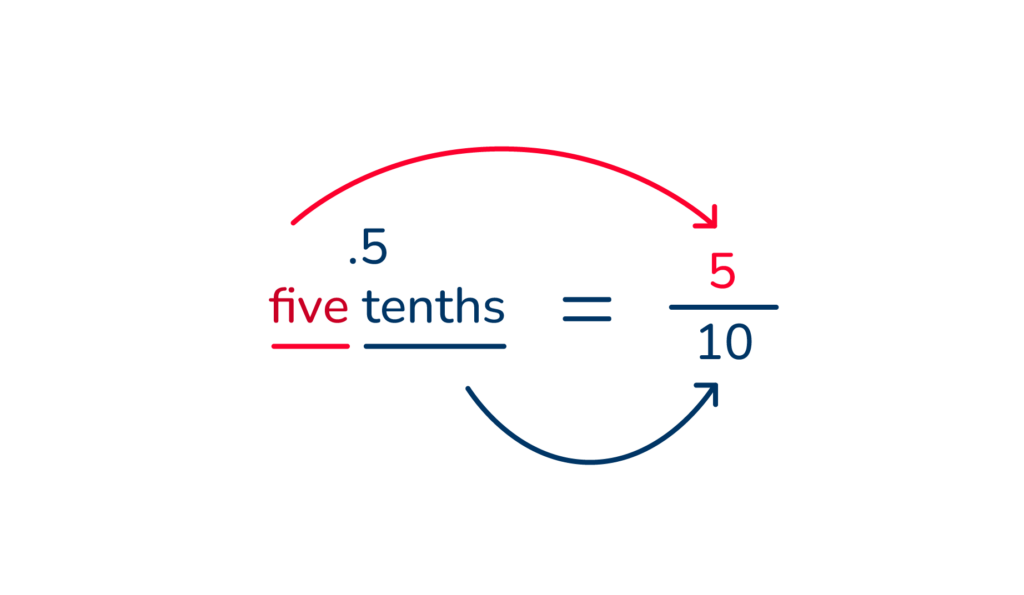
When you read .5 you say, “five tenths”. The 5 is placed on the top of the fraction and 10 on the bottom.”

When converting decimals to fractions, how do we know to say hundredths? tenths? or thousandths? This is where understanding place values come in.

Let’s briefly go over the most common place values found in decimals. Then we can review how to convert decimals to fractions using place values.

Place Values in Decimals

The most common decimals have up to three place values: tenths, hundredths, and thousandths place.

The place value of the last digit will be the number used as the denominator, or bottom number, of the fraction.

Denominator Rules:

When the last digit in the decimal is in the tenths place– the denominator will be 10.
When the last digit in the decimal is in the hundredths place– the denominator will be 100.
When the last digit in the decimal is in the thousandths place– the denominator will be 1000.

Then how do we get the numerator or the number on top of the fraction? Use the number words prior to the place value words. Let’s practice this together a few times:

What numbers would you use as the numerators and denominators when converting each decimal to a fraction?

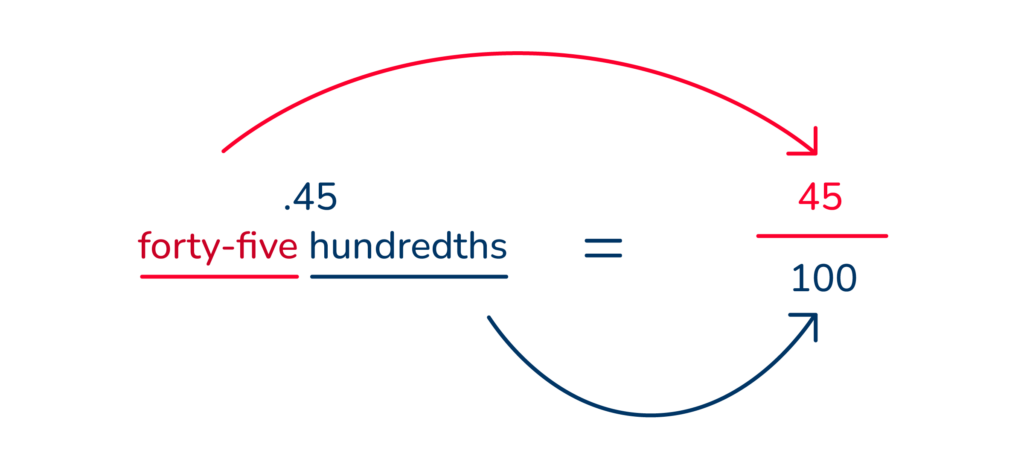
.45 ‘forty-five hundreths’

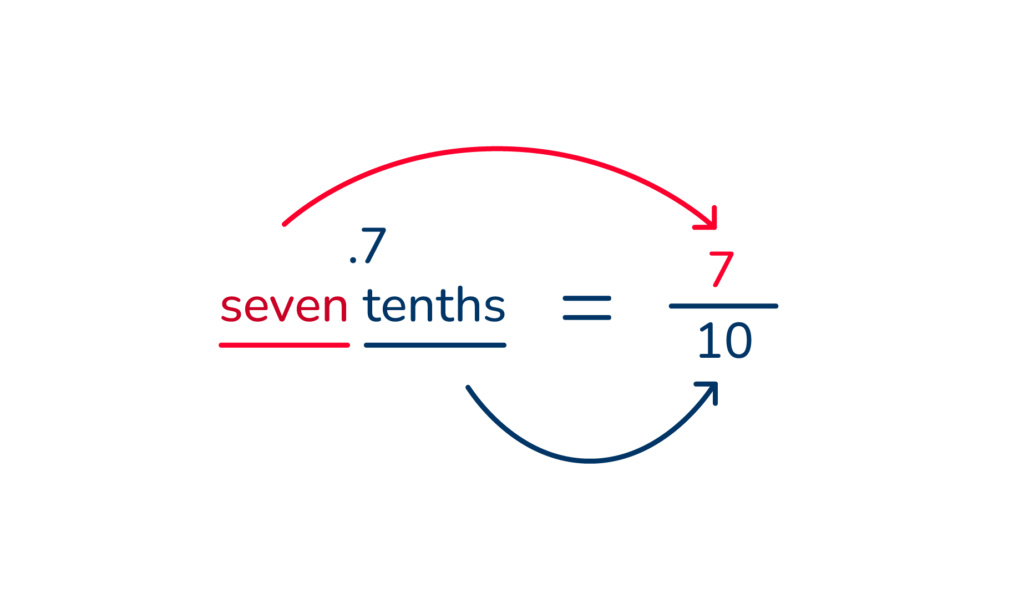
.7 ‘seven tenths’

.865 ‘eight hundred and sixty-five thousandths’

Let’s put these steps together to see how to convert decimal to fraction equivalents.

How to Convert Decimals Step by Step

When converting decimals to fractions the very first step is to read the decimal.

Ask yourself when reading this decimal, did I use the word tenth, hundredth, or thousandth?

Second, depending on which decimal place value word is used when reading the decimal and what place value the last digit is in, use that as the denominator. Either 10, 100, or 1000.
Finally place the entire number word on top as the numerator.
Reduce the fraction if possible.

How to Reduce a Fraction

Reducing a fraction means changing a fraction to its simplest form.

We reduce a fraction by

1. Finding the (Greatest Common Factor) GCF of the numerator and the denominator.
2. Then we divide the numerator and denominator by that number.

For example: How to reduce the fraction 2/4? The GCF of 2 and 4 is 2. So we would divide the top and bottom numbers by 2 and get ½.

Let’s see how this is done with the decimal .95.

1. When reading the decimal .95 we would say, “ninety-five hundredth”. The reason we chose the word hundredth, is because the last digit “5” is in the hundredths place.

2. Because the last digit 5 is in the hundredths place, 100 will be our denominator.

3. Our numerator, or top number, will be the number word: ninety-five.

4. Now we reduce. The GCF of 95 and 100 is five. So, we divide the top and bottom numbers by 5 to get 19/20 as our final fraction.

Converting Decimals to Fractions Chart

The more you convert decimals to fractions, the more you will remember what decimals are as fractions. Would you like a sneak peek of the most common decimal-to-fraction conversions?

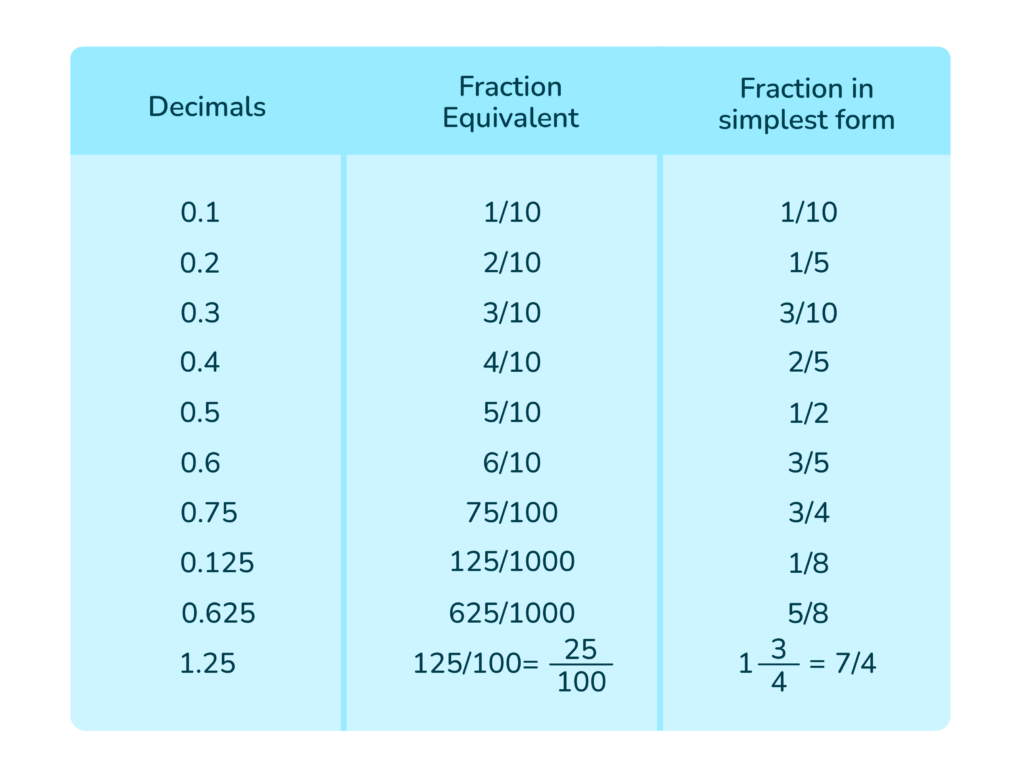
Advanced Decimal to Fraction Conversion

Converting Repeating Decimals to Fractions

What do you do when you are given a repeating decimal? Can the same steps apply? Yes! But we must remember that any fraction you create using these steps will only be an estimate. Let’s see how this can be done.

Convert the repeating decimal of .333333… to a fraction.

First, you must choose an ending point for your decimal. Let’s choose two decimal places .33. Then, you can follow the same 4 steps.

1. When we read the decimal .33 we read “thirty-three hundredths” because the last three is in the hundredths place.

2. Since the last decimal is in the hundredths place, the denominator will be 100.

3. The number word before the word hundredth is “thirty-three” so that will be our numerator.

4. Our final fraction will be 33/100. It can not be reduced.

We have to remember, when converting repeating decimals to fractions in this way, our fractions will be an estimate. The fraction 33/100 is exactly equal to .33 not .3333333 repeating. But it gets us close enough to use as a fraction.

There is a way to get a perfectly equivalent fraction. However, it may take a bit more practice to master.

Converting Decimals to Mixed Number Fractions

What if we wanted to convert a decimal with a whole number such as 3.65? Do we follow the same step-by-step approach for converting decimals to fractions? Yes. With one added feature. Instead of making a proper fraction, we will make a mixed number. Let’s see how!

1. When we read the decimal 3.65 we say “Three and sixty-five hundredths.” Because the last digit 5 is in the hundredths place.

2. Since the last digit is in the hundredths place, we use 100 as the denominator.

3. The number word “sixty-five” will be used as the numerator of the decimal. Notice we didn’t include the whole number 3 as part of the fraction. Why not? Because 3 is a whole number and will be represented as a whole number.

4. Use 3 as a whole number before 65/100 to get 3 65/100.

Practice problems

Click on the boxes below to see the answers!

Question 1: Convert .279 into a reduced fraction

First, you read .279 as “Two hundred and seventy-nine thousandths”. Because the number ends in thousandths, 1000 is the denominator.
Next, place the number word “Two hundred and seventy-nine” on the top of the fraction as the numerator.
The answer is 279/1000. You can’t reduce it any further.

Question 2: Convert .75 into a reduced fraction

First, we read .75 as “seventy-five hundredths”.
Since the last digit is in the hundredths place, 100 will be the denominator.
We use the number word “seventy-five” and the numerator.
Then we reduce 75/100 to ¾ by dividing the numerator and denominator by the GCF of 25.

Question 3: Convert the decimal .55555 into a fraction by estimating

End the decimal at .55.
When you read the decimal .55 you say “fifty-five hundredths”.
Since the last digit is in the hundredths place, the denominator should be 100.
Use the number word “fifty-five” as the numerator.
Then reduce 55/100 to 11/20.

FAQs About Converting Decimals to Fractions

How do you convert a decimal to a fraction?

First, read the decimal. Whichever place value the last digit is will be the denominator (10, 100 or 1000). Place the number word as the numerator. Finally, reduce the fraction with the GCF if necessary.

How do you convert a fraction to a decimal?

You convert a fraction into a decimal by dividing the numerator by the denominator.