Adding and Subtracting Fractions
Don’t fear fractions– embrace them! Learn how adding and subtracting fractions can help in real world situations.

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- There are different types of fractions – There are like and unlike fractions and equivalent fractions.
- A common denominator is a must – If you’re asked to add or subtract two unlike fractions, you’ll have to find the least common denominator (don’t worry, we’ll review what this is below), and convert each fraction to have matching denominators before you start solving your problem.
- Practice makes perfect – Once you know how to add and subtract fractions, keep practicing to increase your speed and accuracy!
Have a fear of fractions? While they can be a bit tricky, learning how to add and subtract fractions is an important skill to master, and it has a ton of real world applications. Once you master this skill, you can move on to the next level of complex math concepts, such as multiplying and dividing fractions. Let’s dig in to learn more adding and subtracting fractions, and you’ll be ready in no time!
What are fractions?
Simply put, fractions are numbers in between whole numbers. The best way to visualize this is to look at a ruler. Consider the small markings in between 0 and 1. Each marking represents a number, different than a whole number, between 0 and 1. These are called fractions!
Fractions help us be more accurate with amounts and measurements. For example, if you need a piece of wood that’s 1 3/4 long, you can use a ruler to make a mark at 1 3/4 before you cut it.
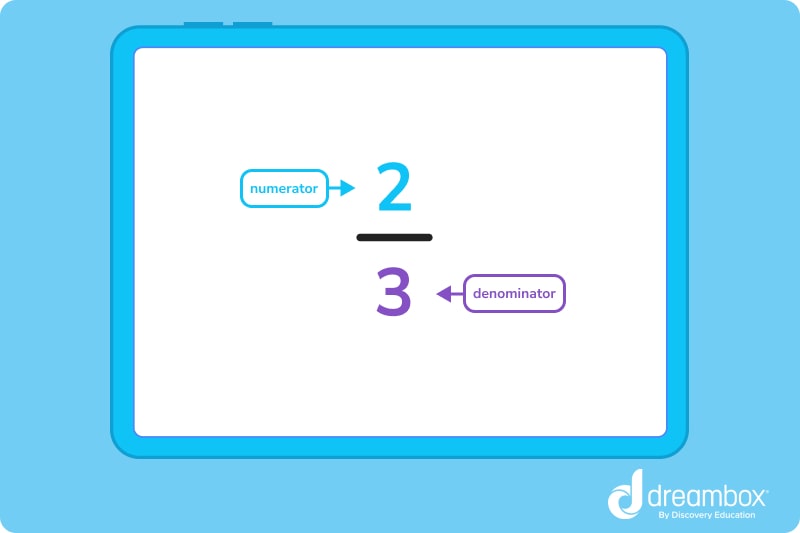
To write a fraction, it’s important to first know about numerators and denominators. The numerator is always the number on top, and the denominator is always the number at the bottom. Here’s a simple example:
Types of fractions
There are three common types of fractions, including:
- Proper — A proper fraction is when the numerator is smaller than the denominator. For example: 1/2 or 3/8.
- Improper — An improper fraction is when the numerator is greater than the denominator. For example: 5/4 or 7/3.
- Mixed — A mixed fraction has a whole number and a proper fraction. For example: 1 3/4 or 3 1/3.
When adding and subtracting fractions, the most common types of fractions used are like and unlike fractions and equivalent fractions. Let’s take a look at each!
Table of contents
Access more math practice with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Like and unlike fractions
Like fractions are fractions with the same denominators — and this is super easy to remember because “like” means “the same” or “similar.” For example, 1/4 and 3/4 are like fractions because they have the same denominator: 4. The 4s in this example are “alike.”
Unlike fractions are fractions with different denominators. Again, an easy way to remember this is to think of the denominators as “different” or “not alike.” For example, 1/3 and 3/4 are unlike fractions because they have different denominators: 3 and 4, respectively.
Equivalent fractions
Fractions that have different numerators and denominators, but are equal to the same value when simplified, are called equivalent fractions. Let’s look at an example of a handful of different fractions that all represent a half — this will be an easy way to remember equivalent fractions!
All fractions in this list represent 1/2 or half, meaning they’re all equivalent fractions:

Defining relevant fraction terms
Before we jump into some examples and steps to adding and subtracting fractions, let’s cover some basic terms that you will come across.
- Common denominator — When the denominators of two or more fractions are the same, they are common denominators.
- Common factor — Factors are numbers we multiply together to get another number. When we find the factors of two or more numbers and then find some factors are “common,” then they are called common factors.
- Least common multiple (LCM) — The LCM is the smallest number that is divisible by both denominators.
- Simplify — In math, simplifying or simplification is when you reduce the expression, fraction, problem, or result to its simplest form.
- Greatest common divisor (GCD) — The greatest common divisor is the greatest number that will divide a given set of numbers equally.
Practical examples of adding and subtracting fractions
Sometimes, fractions can be intimidating! The best place to start is to familiarize yourself with the concept of fractions and why they’re important in the real world.
Let’s picture a pizza that’s cut into 6 slices. You want one piece of pizza, so your portion can be expressed as 1/6 of the pizza. Your friend is hungry and eats 2 pieces of pizza. Their portion can be expressed as 2/6 of the pizza. Now, you’re trying to figure out how much pizza you and your friend have eaten total.
You know that you had 1/6 and your friend had 2/6. Since you’re both eating from the same 6-cut pizza, the denominator is the same, and you simply have to add your portion (1) to your friend’s portion (2) to see how much of the pizza has been eaten: 1 + 2 = 3. You and your friend have eaten 3/6 of the pizza.
In this example, the above problem would be written as:


The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
How to add and subtract fractions, step-by-step
Similar to how we can add and subtract whole numbers, we can add and subtract fractions. First, remember the different types of fractions: like, unlike, and equivalent. One important rule: we can only add and subtract like fractions.
The reason is simple — you cannot add 2 bananas and 3 apples to get 5 bananas because they are not all bananas. It’s the same way with fractions: you can’t add unlike fractions because they have different “denominators” or unit quantities. The same goes for subtraction. You cannot subtract unlike units from one another.
Let’s go through the steps of adding and subtracting fractions together!
Step 1: Make the fractions like fractions
If you’re working with like fractions (such as 1/3 and 2/3), the denominators will already be the same, so you can move to step 2. However, when you’re faced with two fractions with unlike denominators, you will have to make the fractions like fractions. There are two ways you may have to approach this.
A. If one denominator is a multiple of the other denominator….
Let’s use the following example:

In this example, the denominators are different: 4 and 8. However, 8 is a multiple of 4. This means we can multiply 4 x 2 to make it 8. By doing this, the denominators are the same, which makes them like fractions. But, we can’t stop there! 2/8 is not be an equivalent fraction to 2/4 — leaving it as 2/8 makes it an entirely different fraction.
So, we have to also multiply the numerator (2) by the same number we multiplied the denominator by (2). This changes 2/4 to be 4/8. 2/4 and 4/8 are equivalent fractions, and 4/8 and 3/8 are like fractions, so now we are able to add the fractions. The problem now looks like this:
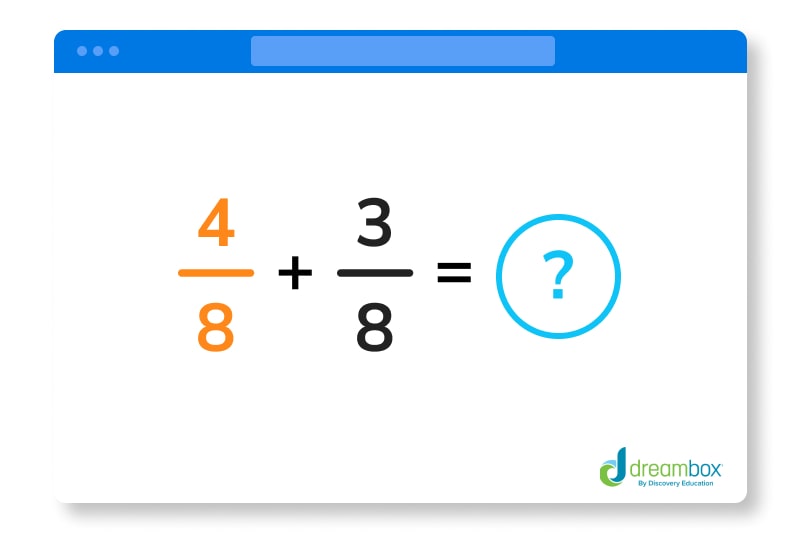
B. If both the denominators have no common factor….
Let’s use this problem as an example:

The denominators are different: 5 and 4. Also, 4 is not a multiple of 5, and 5 is not a multiple of 4. The easiest thing to do here is to multiply both denominators together to find a common factor. So: 5 x 4 = 20. 20 then becomes our new denominator for both fractions.
Remember, you also have to multiply the numerators to convert each equation into an equivalent fraction to keep the equation the same. Here’s how we would do that:

Step 2: Add and subtract the numerators
Once you have like fractions, you are able to add and subtract the numerators. The sum or difference will become the new numerator, while the common denominator discussed in step 1 will remain the same.
Here’s Step 2 from our two examples above — an example of each:
A. 4/8 + 3/8 = ⅞

B. 8/20 – 5/20 = 3/20

Step 3: Simplify the fraction
Sometimes our answers can be simplified into equivalent fractions that use the greatest common divisor. Both of our examples are in their most simplified form, but let’s consider the following example:

When we subtract 3/20 from 5/20, the result is 2/20, which is the correct answer. However, it can be simplified because the numerator and denominator have a common factor: 2. We can always simplify fractions until there are no common factors left between the numerator and denominator other than 1.
Let’s practice by simplifying, or reducing, the fraction 2/20.
2 is a common factor in both the numerator and the denominator, so it can be reduced to its simplified form as follows:

2 goes into 20 ten times.
Let's Practice Together!
1. Find the common denominator of 1/5 and 4/6.
We know that 5 and 6 do not share any common factors, so we must multiply 5 x 6 to find the common denominator. The common denominator of 1/5 and 4/6 is 30.
2. What is the sum of 2/3 + 1/9?
First, we have to make the denominators the same. The original denominators are 3 and 9. 9 is a multiple of 3, so the common denominator is 9.

Then, we can rewrite the problem as 6/9 + 1/9, and add the numerators. Then, we have 7/9. This fraction cannot be simplified, so the final answer is 7/9.
3. 3/8 - 1/7 = ?
First, we have to make the denominators the same. The common denominator will be 8 x 7 = 56.
Now, let’s make each fraction an equivalent fraction.

Then, we can subtract the numerators. So, 21 – 8 = 13. Now, we can write our result as 13/56. This fraction cannot be simplified, so the final answer is 13/56.
Ready to give it a go?
-
Now that we know about the different types of fractions, how to find the common denominator, and how to add and subtract fractions, we’re ready to do a few more practice problems to put our new skills to the test! Work through the following problems on your own. Feel free to look back at the practice problems above if you get stuck or if you need a quick reminder on how to add and subtract fractions.
And remember, don’t get discouraged if you run into a roadblock! Practice is the best way to learn something new.
Practice Problems
Click to reveal the answer.
The sum is 23/20.
The result is 1/15.
The common denominator is 10.
The equivalent fractions would be 5/10 and 2/10.
The simplified fraction is 1/3.
Parent Guide
-
1. The sum is 23/20. How did we get here?
- 1. First, we need to find the common denominator. In this case, the common denominator for 4 and 5 is 20.
2. Then, convert both fractions into equivalent fractions with a denominator of 20.
3. To convert 3/4 to have a denominator of 20, we need to multiply both the numerator and the denominator by 5. This gives us (3 x 5) / (4x 5) = 15/20
4. To convert the second fraction, 2/5, to have a denominator of 20, we need to multiply both the numerator and the denominator by 4. This gives us (2 x 4) / (5 x 4) = 8/20
5. Next, we add the fractions now that both have been converted to equivalent fractions. Add the numerators 15 + 8, and keep the denominator the same. This gives us 23/20.
6. This is the most simplified version of this fraction, so the final sum is 23/20. You can also write the answer as a mixed fraction: 1 3/20 -
2. The result is 1/15. How did we get here?
- 1. First, we need to find the common denominator of 3 and 5, which is 15.
2. Then, we have to convert both fractions into equivalent fractions.
3. To convert 2/5 to have a denominator of 15, multiply both the numerator and denominator by 3. So, 2/5 = (2 x 3) / (5 x 3) = 6/15.
4. To convert 1/3 to have a denominator of 15, multiply both the numerator and denominator by 5. So, 1/3 = (1 x 5)/(3 x 5) = 5/15
5. Now, both fractions have a common denominator of 15, so we can subtract the numerators, 6 – 5, to get 1.
6. 1/15 is the result and cannot be simplified. -
3. The common denominator is 10. How did we get here?
- 1. We know that 2 and 5 are the denominators, and they do not share any common factors.
2. We must multiply 2 x 5 to find the common denominator. The common denominator is 10.
3. 2 x 5 = 10 -
4. The equivalent fractions would be 5/10 and 2/10. How did we get here?
- 1. First, multiply both the numerator and the denominator in 1/2 by 5 because it’s the opposite denominator of 2 that we used to find the common denominator 10.
2. 1 x 5 = 5 and 2 x 5 = 10. The equivalent fraction of 1/2 is 5/10.
3. Second, multiply both the numerator and the denominator in 1/5 by 2 because it’s the opposite denominator of 5 that we used to find the common denominator 10.
4. 1 x 2 = 2 and 5 x 2 = 10. The equivalent fraction of 1/5 is 2/10. -
5. The simplified fraction is 1/3. How did we get here?
- 1. 60 is a multiple of 20.
2. 20 goes into itself one time, giving us a numerator of 1.
3. 20 goes into 60 three times, giving us a denominator of 3.
FAQs about adding and subtracting fractions
Fractions are a way of representing a part of a whole or a division of a quantity. They are used to express numbers that are not typically whole numbers, but, rather, they represent a portion or a ratio of a whole. A fraction consists of two numbers separated by a slash (“/”) or a horizontal line. The number above the line is called the numerator, and it represents the part or quantity being considered. The number below the line is called the denominator, and it represents the total number of equal parts into which the whole is divided.
The rule for adding and subtracting fractions involves finding a common denominator and then performing the operation based on that denominator. Here are the step-by-step instructions:
- Find a common denominator: The denominators of the fractions you’re working with need to be the same. If the denominators are already the same, you can skip this step. Otherwise, you need to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that is divisible by both denominators.
- Convert the fractions: Once you have a common denominator, you need to convert each fraction so that it has that common denominator. To do this, you multiply both the numerator and denominator of each fraction by the same number that will make the denominator match the common denominator.
- Perform the operation: For addition, you add the numerators of the fractions together and keep the common denominator. For subtraction, you subtract the numerators of the fractions and keep the common denominator.
- Simplify, if necessary: After performing the operation, you may need to simplify the resulting fraction. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator, and divide both the numerator and denominator by the GCD.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

