Converting Fractions to Decimals
Get straight to the point with our easy-to-use guide on how to turn fractions into decimals.

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- Decimals always mean that you’re working with parts of a number – While you can write whole numbers as decimals, a decimal itself is always less than a whole number. For example: 3.2 is a decimal, but on its own, it is not a whole number. However, 10.0 is a whole number, as there are no numbers to the right of the decimal.
- While your answers look “different,” they hold the same value – Converting means presenting your answer differently. Even though your answers will look different to the eye, they equal the same value in math.
- There are two main ways to convert – These methods are known as the Power of 10’s method and the long division method. We go over both below, helping you to do your conversions without a calculator.
Does your heart sink when the teacher tells you to leave your answer in decimal form? Don’t worry! Converting fractions to decimals doesn’t have to be a scary process. In fact, as you get older, it might be even easier than trying to figure out fractions.
Today, we’re going to help you convert fractions to decimals with confidence. Let’s dive in.
Converting fractions to decimals: why is it important?
Have you ever seen signs at the store that say something like “get 50% off” or “25% off after your first purchase”? Your parent or guardian gets all excited because they know they get to save money, and you might get more clothes or toys!
It’s important to know how to convert fractions into decimals so you can understand what these percentages really mean. If you know that 50% equals ½, then that means you can say to mom or dad, “Hey, since the sign says everything is 50% off today, can I get two toys instead of one?”
Or maybe you’re trying to figure out what your grade will be on a report card. Grades are usually calculated as percentages, like 75% or 100%. But, let’s say your teacher tells you that, on one of your spelling tests, you got 14/16 of the questions right. Well, what does that mean?!?
Once you figure out how to convert fractions to decimals, you’ll be able to answer that question in seconds.
So what are we waiting for? Let’s start learning!
The different methods of converting fractions to decimals
The best part about converting fractions to decimals? There are plenty of ways to do it!
We’ll walk you through some of the best methods below. Pick your favorite method to use, then absolutely ace your next math test!
Table of contents
Access more math practice with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

The long division method
Did you know? You can actually use division to get your conversion done — in fact, you can look at a fraction as a division problem!
There are a few key steps you need to follow in order to convert a fraction into a decimal using division. Keep in mind that you can add as many 0’s as you need behind a whole number to help solve your division problem.
EXAMPLE: Convert 4/15 into decimal form.
1. Identify your numerator and denominator – Remember, the numerator is the number on the top of a fraction and the denominator is the number on the bottom. Here, our numerator is 4 and our denominator is 15.
2. Write the fraction as a division problem – Place the 15 outside the division bracket, and place 4 inside the bracket. Then ask: “How many times can 15 go into 4?”
3. The answer is “no times,” so we have to make 4 bigger than or equal to 15 – Add a 0 behind the 44, giving us 15 ⟌40.
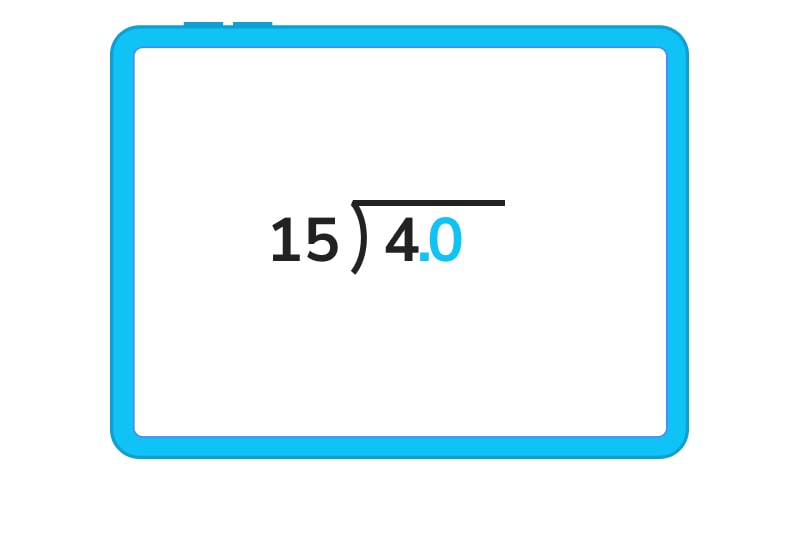
Keep in mind that this is really 4.0, with the decimal point between the 4 and the 0, but to divide, you can think about it as the number 40. Just remember that the answer will be placed in the tenths place of the quotient as the first digit of your decimal answer (this will make more sense below!)
4. Now, we have to determine how many times 15 can go into 40 – Since we can do this twice, our quotient is 2.

5. Start the long division process – We multiply 15 by 2 and get 30. Place the 30 beneath the 40, then subtract. You should get an answer of 10.

6. Since 10 is smaller than 15, we can add another 0 behind the decimal in our dividend – That way, we can keep dividing with a larger number to make it a little bit easier.

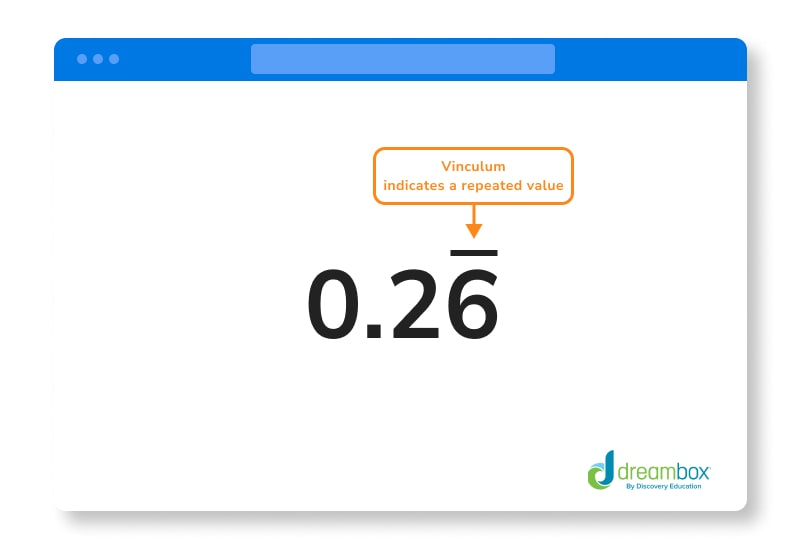
7. Solve the revised problem of 15⟌100 – 15 goes into 100 six times, giving us a quotient of 6 and a remainder of 10 after we finish our division operation. Our quotient, at this point, should look like 0.26 — and our equation is back to 15/10.

8. Continue the process and notice – If you keep going, you will notice that we keep dividing into 10, adding a 0 to divide into 100, getting a quotient of 6, and then having yet another remainder of 10.
This value is going to be a “repeated value,” meaning no matter how many times we drop a 0 down and complete the division process, we will always have a remainder of 10. We note the answer as 0.2666666666 or with a figure called a “vinculum” above the 6, which indicates a repeated value. This looks like:

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Changing the denominator to a power of 10
To change a fraction into a decimal, you can also change your denominator using the powers of 10.
Why do this, you ask? Well, it’s an easier way to change your number to decimal form.. For example: A value of 9/10 can be understood as 0.9 and a value of 45/100 can be understood as 0.45 — which are easier to work with.
Let’s see this in action below!
EXAMPLE: 2/5
- First, identify the numerator and denominator – In our example, the numerator is 2 and the denominator is 5.
- Change our fraction into an equivalent fraction that has a power of 10 denominator such as 10, 100, or 1000 – Identify a number we could multiply by to change our denominator into a power of 10. In this case, 5 can be multiplied by 2 to get 10.
- Multiply the numerator (top number) by the same number that you multiplied the denominator by – This gives us the equivalent fraction of 4/10.
- Convert – The fraction 4/10 literally means we have 4 tenths, meaning the number 4 should live in the tenths position in our decimal. Write this as 0.4.
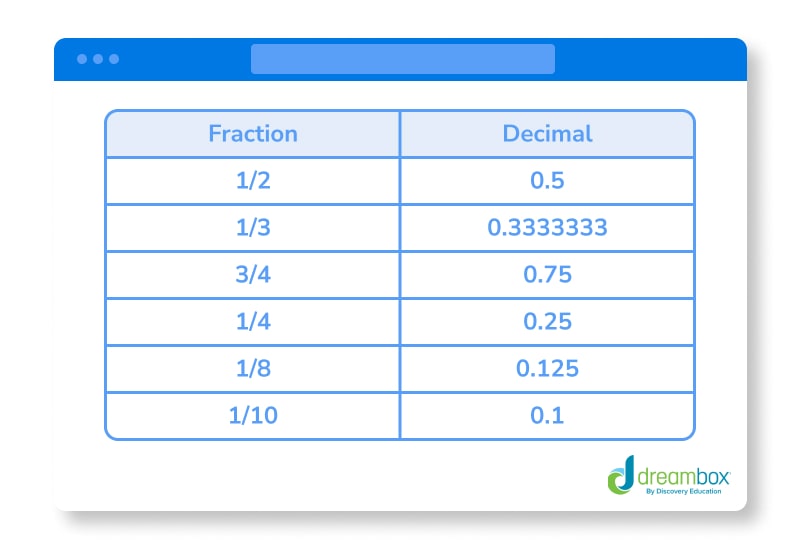
Common fraction to decimal conversions
Now that you know how to convert fractions to decimals, it’s time to take a look at some common conversions you can memorize. Knowing these common conversions makes your math homework so much easier — which is why we’ve put this handy table together for you to look at any time you need it.
Let's Practice Together!
1. Convert ⅗ using the long division method
3/5 (via long division method)
- First, we identify our numerator and denominator. In this case, 3 is our numerator and 5 is our denominator. We set it up in the division bar, as so: 5⟌3. Since 5 does not go into 3, we will put a decimal point in our quotient to indicate that our final answer will be a decimal: 0.. Leave the space behind the decimal point blank, since you will fill in your answer behind it.
- Since 5 doesn’t go into 3, we can add a 0 behind the 3, making it 3.0. Now, think of the division as 30 divided by 5, which = 6.
- The 6 will be written in the tenths place, since we are dividing into the tenths place of our dividend. The quotient will look like 0.6.
- Since the remainder here is 0, our process to convert is complete. ⅗ = 0.6.
2. Convert 4/10 to a decimal using the power of 10s method
4/10 (via power of 10’s method)
- First, we identify the numerator and the denominator – For this problem, our numerator is 4 and our denominator is 10. We recognize that our denominator is already a power of 10, which will make our conversion to a decimal easy!
- 4/10 means you have 4 tenths, or rather 4 in the tenths place of your decimal. So, 4/10 can be written as 0.4.
- This can be expressed as a quotient of 0.4.
3. Convert 4/25 to a decimal using the long division method
- First, we identify the numerator and the denominator. For this problem, our numerator is 4 and our denominator is 25. We arrange them in the division bar, like this: 25⟌4. We’ll also add a 0. in our quotient, indicating that our final answer will be a decimal.
- 25 cannot divide into 4, so we can add a decimal point and 0 behind the 4 so it appears as a 40.
- 25 can go into 40 once, so we write a 1 in the tenths position of our quotient, multiply 1 by 25 to get 25, and subtract that from 40. Our difference is 15.
- Bring down another 0, so 15 appears as 150. We know 25*6 = 150 so we can put a 6 in the hundredths position of our quotient. There is no remainder so we are done, and our answer is 0.16!
4. Convert 2/7 to a decimal using the long division method
- First, we identify the numerator and the denominator. For this problem, our numerator is 2 and our denominator is 7. We arrange them in the division bar, like this: 7⟌2. We’ll then add in a 0. in the quotient area, indicating that our final answer will be a decimal.
- Since 7 can’t go into two, we can add a 0 behind the 2 to make it a 2.0.
- Now we see how many times 7 goes into 20. We know it can go in twice, leaving us with a product of 14.
- We do the division steps, winding up with a remainder of 6. We notate this as a 0.2 above the division bar, and we drop down a 0 — making our 6 a 60.
- We know that 7 goes into 60 8 times. We do the division steps, finding a remainder of 4. We note this as a quotient of 0.28, bringing down a 0 to turn our 4 into a 40. Our new problem reads 7⟌40.
- We know that 7 goes into 40 a total of 5 times. We do the division steps and notate this with a quotient of 0.285, with a remainder of 5. Our new problem reads 7⟌50.
- While this can be simplified further, generally, you’ll stop after you reach a decimal quotient that is completed three places after the decimal point. If you’re not sure if you need to simplify it further, you can always ask your teacher.
5. Practice problem 5
3/10 (via power of 10’s method)
- First, we identify our numerator and denominator. In this case, 3 is our numerator and 10 is our denominator.
- Since 10 is already a power of 10, we can easily change our fraction into decimal form. 3/10 is the same as saying 3 tenths, meaning we have a 3 in the tenths place as our decimal. We write this as 0.3.
- You’re done!
Ready to give it a go?
-
Ready to do it on your own? We’re sure you’ll knock it out of the park! Don’t be afraid to mess up and get back up after…it’s all part of the learning process.
Speaking of the learning process, the only way to keep going is to — wait for it — practice! We’ve put together a few more problems to help you master the art of converting fractions to decimals.
We know you’re going to ace your next math test after you perfect this math superpower!
Practice Problems
Click to reveal the answer.
Parent Guide
-
1. The answer is 0.2. How did we get here?
- 1. Identify your numerator (2) and denominator (10). Set them up with the division bar (10⟌2).
2. Now, place a decimal in your quotient (you should have 0._ when you do this) to indicate that it will be a decimal conversion.
3. Since 10 can’t go into 2, we drop down a 0. Divide 10 into 20. You should be able to do this twice.
4. We do the division steps to confirm and note this as 0.2 in the quotient, resulting in a remainder of 0. You’re done! -
2. The answer is 0.4. How did we get here?
- 1. Identify your numerator (2) and your denominator (5). Determine what you need to multiply 5 by to be a power of 10 (i.e., 10, 100, 1000).
2. The number to multiply both your numerator and denominator by is 2. This will change your fraction into the equivalent fraction of 4/10.
3. We can now translate that value into the decimal version (0.4), since the fractions show a value of 4 tenths.
4. You’re done! -
3. The answer is 0.25. How did we get here?
- 1. First, identify your numerator (5) and denominator (20). Arrange under the division bar, like so: 20⟌5. You should have 0. as your quotient at this stage, indicating that it’s a decimal conversion.
2. Ask yourself: Does 20 go into 5? It does not, so we have to drop a 0 down to turn our 5 into a 50. The new problem is: 20⟌50.
3. 20 goes into 50 twice. We do the division steps, notating this with a new quotient of 0.2. We are left with a remainder of 10.
4. 20 cannot go into 10, so we drop a 0 to turn our 10 into 100. Our new equation is 20⟌100.
5. 20 goes into 100 a total of 5 times. We do the division steps, notating a new quotient of 0.25. We have no remainder, meaning we are done with the problem. -
4. The answer is 0.75. How did we get here?
- 1. First, identify your numerator (3) and denominator (4). Arrange under the division bar, like so: 4⟌3. You should have 0. as your quotient at this stage, indicating that it’s a decimal conversion.
2. Ask yourself: Does 4 go into 3? It does not, so we have to drop a 0 down to turn our 3 into a 30. The new problem is: 4⟌30.
3. 4 goes into 30 7 times. We do the division steps, notating this with a new quotient of 0.7. This leaves us with a remainder of 2.
4. 4 cannot go into 2, so we drop a 0 to turn our 2 into 20. Our new equation is 4⟌20. <5. 4 goes into 20 a total of 5 times. We do the division steps, notating a new quotient of 0.75. We have no remainder, meaning we are done with the problem. -
5. The answer is 0.5. How did we get here?
- 1. First, identify your numerator (5) and denominator (10). Determine what you need to multiply 10 by to be a power of 10 (i.e., 10, 100, 1000).
2. The denominator is already a power of 10, so we can simply write the fraction in decimal form. 5/10 is the same as having 5 tenths. This means you can keep it simple and write a 5 in the tenths place, leaving you with 0.5 as your final answer.
FAQs about converting fractions to decimals
While a calculator can be handy, you do not need one to properly convert fractions to decimals. In fact, it’s often better to learn without one so you have the math skills mastered going forward.
Often, you’ll find that the easiest way to convert quickly is to use a calculator or pen and paper to divide the numerator by the denominator.
1/16 in decimal is 0.0625.
A decimal point indicates fractional numerical elements that are not whole numbers. They are listed to the right of the decimal point, in the respective tenths, hundredths, and thousandths places (and so on).
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

