Dividing Fractions in 5 Easy Steps
Dealing with fractions can be difficult, and dividing fractions is no different. Let’s learn how to divide fractions in 5 easy steps.

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- You want to use steps to divide fractions – If you try to do it all at once, it might get confusing. Separate the process into steps.
- Know your terminology – Know the difference between the numerator and the denominator before you start working on your division problems.
- Use visual guides to help you – Using visual aids to help you figure out how to divide fractions can be a great way to learn more effectively.
Fractions are already parts of a whole number. So, you might be wondering: how can you divide a fraction into an even smaller part—or, for that matter, divide it to turn it into an even bigger part?
Honestly, it works the same way dividing whole numbers works. You can divide a small number into an even smaller number, right? 4 divided by 2 gives you 2. So how can ¼ divided by ½ give you ½? Today, we’re going to walk through how to divide fractions in 5 easy steps. But first, let’s make sure we understand the basics to make it super easy to follow along.
The parts of a fraction
Unlike a whole number, a fraction has two parts.
- The numerator – This is the number on the top of the fraction. If you think of a fraction as shaded parts of a whole, it is how many sections you would shade in.
- The denominator – This is the number on the bottom of the fraction. So, using the example of a fraction as shaded parts of a whole, it would be how many sections available to shade in.
Visually, 1/4 would look like this, with 1 out of 4 parts shaded in.

And 3/16 would look like this, with 3 out of 16 parts shaded in.
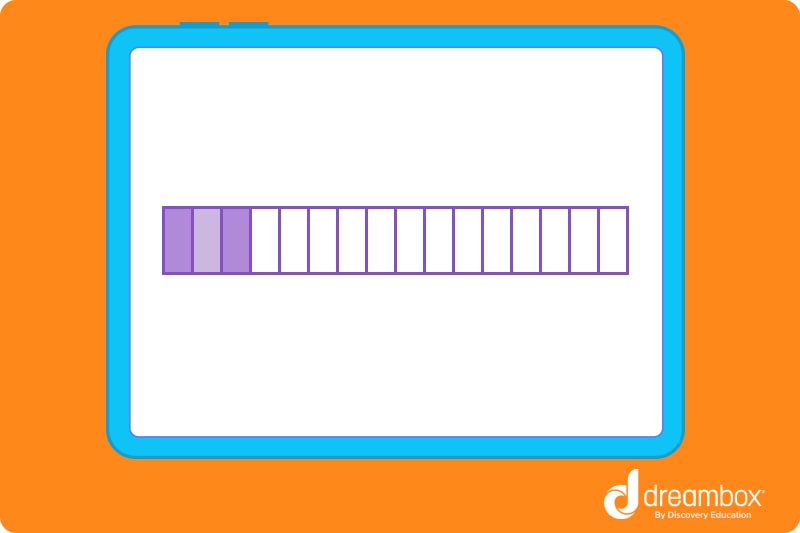
Table of contents
Practice more division with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Dividing fractions in 5 steps
There are several different ways to divide fractions, but if you try to master them or use them all at once, it might get super confusing. It’s always best to divide complicated ideas into smaller parts to make the ideas easier to understand. Let’s DIVIDE (ha, see what we did there?) dividing fractions into 5 easy steps to help make it easier.
1. Read the problem
It might sound simple, but first, you need to understand what you’re being asked to do. Let’s look at the following problem:

Basically, you’re being asked to divide five-sixths by seven-eighths.
2. Keep the first fraction as is
Next, you need to know what to do with each of the fractions in the problem. Do not do anything to the first fraction. Keep it EXACTLY as it is.

3. Change the division sign to a multiplication sign
You mean I have to know how to multiply to know how to divide? Absolutely you do! What you want to do in this step is to change the DIVISION sign to a MULTIPLICATION sign.
So, if we were just rewriting the problem and this was our final step, the problem would look like this:

But it ISN’T the last step. The last step is…
4. Flip the second fraction
The last step before you can solve the problem is to flip the numerator with the denominator in the second fraction. So, now your problem looks like this:

5. Solve by multiplying the numerators and denominators together, then simplify if necessary

The answer is 16/9, which cannot be simplified, so it remains the same.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Ready to give it a go?
-
Dividing fractions is pretty simple, right? Just keep that in mind…keep dividing fractions as simple as possible. The only person who can get you confused is you!
Ready to practice on your own? We’ve included some no-risk practice problems to get you ready for the classroom!
Dividing Fractions Practice Problems
Click to reveal the answer.
The answer is 15/6, and since both 15 and 6 can be divided by 3, the answer, when simplified, will be 5/2.
The answer is 16/15. This cannot be simplified, as these numbers cannot be divided by a similar number.
The answer is 4/3. This is simplified from 24/18, numbers that can each be divided by 6 to give you 4/3.
The answer is 12/7. This cannot be simplified, as these numbers cannot be divided by a similar number.
The answer is 7/4, simplified from 14/8, which can both be divided by 2 to give you the answer.
Parent Guide
-
1. The answer is 15/6, and since both 15 and 6 can be divided by 3, the answer, when simplified, will be 5/2. How did we get here?
- 1. Read the problem: 5/6➗1/3
2. Keep 5/6 as is.
3. Change the division symbol to a multiplication symbol.
4. Flip 1/3 to 3/1.
5. Then, multiply 5 by 3 to get 15 and 6 by 1 to get 6, which equals 15/6. Divide each of these by 3 to get 5/2. -
2. The answer is 16/15. This cannot be simplified, as these numbers cannot be divided by a similar number. How did we get here?
- 1. Read the problem: 4/5➗3/4
2. Keep 4/5 as is.
3. Change the division symbol to a multiplication symbol.
4. Flip 3/4 to 4/3.
5. Then, multiply 4 by 4 to get 16 and 5 by 3 to get 15, which equals 16/15. -
3. The answer is 4/3. This is simplified from 24/18, numbers that can each be divided by 6 to give you 4/3. How did we get here?
- 1. Read the problem: 8/9➗2/3
2. Keep 8/9 as is.
3. Change the division symbol to a multiplication symbol.
4. Flip 2/3 to 3/2.
5. Then, multiply 8 by 3 to get 24 and 9 by 2 to get 18. Both of these can be divided by 6, which leaves you with 4/3. -
4. The answer is 12/7. This cannot be simplified, as these numbers cannot be divided by a similar number. How did we get here?
- 1. Read the problem: 3/7 ➗1/4
2. Keep 3/7 as is.
3. Change the division symbol to a multiplication symbol.
4. Flip 1/4 to 4/1.
5. Then, multiply 3 by 4 to get 12 and 7 by 1 to get 7, which equals 12/7. -
5. The answer is 7/4, simplified from 14/8, which can both be divided by 2 to give you the answer. How did we get here?
- 1. Read the problem: 7/8➗1/2
2. Keep 7/8 as is.
3. Change the division symbol to a multiplication symbol.
4. Flip 1/2 to 2/1.
5. Then, multiply 7 by 2 to get 14 and 8 by 1 to get 8, then simplify 14/8 to 7/4.
FAQs about dividing fractions
To divide fractions, you multiply the first fraction by the reciprocal (flipped version) of the second fraction. The reciprocal of a fraction is obtained by swapping the numerator and denominator. For example, to divide 1/2 by 3/4, you multiply 1/2 by 4/3. The result is (1/2) × (4/3) = 4/6, which simplifies to 2/3.
If the divisor is a whole number, you can convert it to a fraction by putting it over 1. For example, if you want to divide 3/4 by 2, you can rewrite it as 3/4 ÷ 2/1. Then, you proceed with the division using the reciprocal: (3/4) × (1/2) = 3/8.
Yes, the dividend can be a whole number! In division, the whole number is treated as a fraction with a denominator of 1. For example, if you want to divide 2 by 3/4, you can rewrite it as 2/1 ÷ 3/4. Then, you proceed with the division using the reciprocal: (2/1) × (4/3) = 8/3.
To simplify the result, reduce the fraction to its simplest form by dividing both the numerator and denominator by their greatest common divisor. For example, if the result of dividing fractions is 12/16, you can simplify it by dividing both the numerator and denominator by 4. The simplified form is 3/4.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

