Measuring Angles
Get it right with your right angles in this easy measurement guide!

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- We measure angles in degrees – Just like you’d use inches or centimeters to measure length on a ruler, we use degrees when we measure angles.
- You’ll need special tools – To measure angles correctly, you’ll need a protractor. You can get these from any big box store or office supply.
- Sometimes radians might be used in place of degrees – You might be asked to use radians as your unit of measurement instead of degrees, so pay careful attention to your assignment directions!
Learning how to measure angles is one of the most important skills you’ll learn to prepare you for geometry and higher-level math classes. It’s simple to do once you’ve got the right tools and know-how — and we’re here to walk you through it!
Here’s our helpful step-by-step guide to measuring angles.
Basic units in angle measurement
Here are some basic terms to keep in mind as you practice measuring angles.
The degree
Students generally will be familiar with the measurable unit of a degree — especially if they’ve had experience setting the temperature on an oven or determining how cold it is outside.
However, that’s not the type of degree we’re referencing when we say “degree” or “degree angle” when measuring angles. Instead, we’re applying a secondary, separate meaning and using it as a unit of measurement for angles that are measured by a protractor.
You’ll still use the degree symbol (°), or you can simply write “degrees” after your answer to clarify and finish it.
The radian
Radians aren’t something most third and fourth grade students are familiar with yet. However, they will run into it later on — so we wanted to mention it here.
Radians are another unit of measurement that can be used in place of degrees when we measure angles. You’ll use these more in higher level math classes and applied math classes (like physics) — so simply knowing the difference between the two is good enough for now.
Comparison between degrees and radians
You know that degrees and radians are different forms of measurement…but you’re likely wondering: How are they so different?
While both can be used to measure angles, degrees are slightly more “basic” than radians — they can be measured using a protractor (just like we’d see an inch mark on a ruler do).
Radians are a little more complex of a unit and can do more in higher level math. The formal definition states that they represent a ratio, otherwise known as the relationship between two different quantities.
This ratio is then divided by the length of the radius of a shape, which is normally a circle or a circular shape.


Table of contents
Access more math practice with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

How to measure angles
The first step to a correct calculation is getting accurate measurements on those angles.
Here’s our helpful how-to for kids, covering instructions for protractor measurement.
Using a protractor
- Grab your protractor, and give it a quick look. You should identify the midpoint, otherwise known as the middle point of your protractor. This is usually marked with a small dot so it’s easy to see.
- Line it all up. Line up your angle in line with the “0” line of your protractor, which can be both on the right (bottom) and left (top) areas of your protractor. You can use either, choosing the one that lines up best with your angle.
- You might run into “upside-down” angles later on in your math career. While this guide only focuses on how to measure basic angles you’ll see now, you can look forward to learning how to move your protractor around the angle to get the most accurate measurement later on!
- Read off the measurement. You’ll then use the numbers on either side of your protractor’s dividing line to judge the measurement of the angle. You’ll choose whichever value is pointed to by the other ray of the angle that is not aligned with the 0 marker.
Types of angles
There are many different types of angles you’ll see as you practice measuring angles. Here are a few key types to remember as you practice your measurement:
Acute angle
Acute angles are angles where the measure of the angle is greater than 0° but less than 90°. These angles will look narrow, like fingers pinching something small. An easy way to remember these is to think that they are small, tiny, and, generally, look “cute.”

Obtuse angle
An obtuse angle is larger, measuring between 90° and 180°. Think of obtuse angles as large, or looking like “wide-open” mouths ready to chomp on your pencil.

Right angle
Right angles are mathematically defined as angles that are exactly 90° — no more and no less. You can identify them by their clean, sharp appearance, with the two lines or rays creating a “box like” angle at the vertex, where they meet.
Straight angle
Straight angles are simple — they are defined as angles that are exactly 180°, which means that they’ll look like a straight line on your paper.


The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Angles in real life
Angles aren’t just something you’ll see on worksheets or homework packets. They’re actually all around us in our daily lives! Our suggestion is to take an “angle hunt” around your house to see how many you can find. Doing this will help you to easily identify angle types, which is a great starting point for other types of angle measurement later on. You won’t even need an actual protractor to spot them!
Not sure where to start? Here are a few places that likely have angles around your home:
- Steps or stairs
- Books, binders, or folders
- Door frames and doorways
- Walls and baseboards
- Boxes and packages
- Certain foods (like lasagna noodles)
Go take a quick walk, and see what you can find. Don’t forget to tell yourself “good work” after!
Let’s practice together!
1. Measure the given angle:
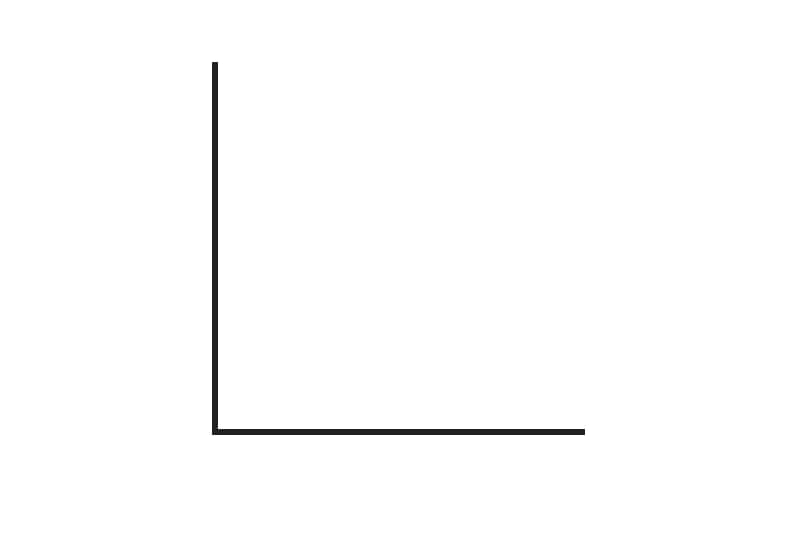
- Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
- This angle appears to be a right angle, which is an angle designation that can only be given to angles that have a measurement of 90°.
- We check our work, aligning the protractor’s midpoint at the vertex of the angle.
- We then align the flat base line of the angle with the “0” mark on the protractor.
- We read the measurement off of the value that the second vertical line is pointing to, which reads 90°.
- We’re done!
2. Measure the given angle:

- Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
- This angle appears to be a straight angle, which is an angle designation that can only be given to angles that have a measurement of 180°.
- We check our work, aligning the protractor’s midpoint at the vertex of the angle.
- We then align the flat base line of the angle with the “0” mark on the protractor.
- We read the measurement off of the value that the line is pointing to, which reads 180°.
- We’re done!
3. Measure the given angle:
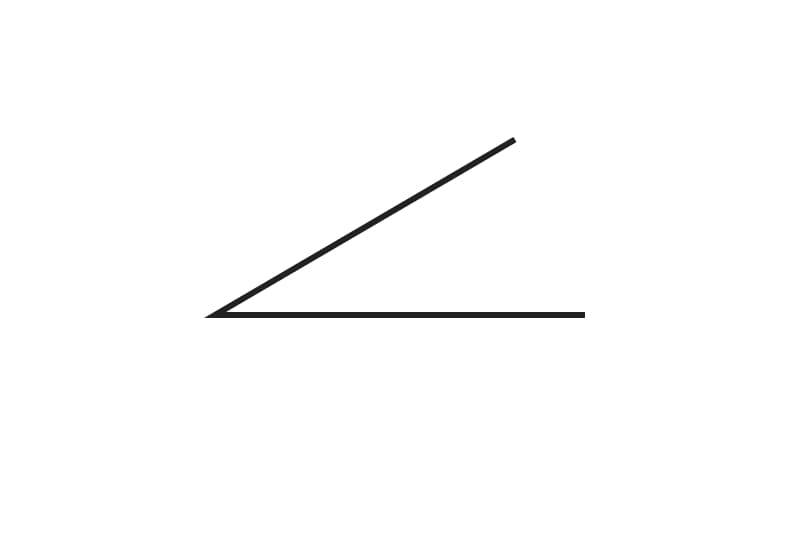
- Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
- This angle appears to be an acute angle, which is an angle designation that can only be given to angles that have a measurement of less than 90°.
- We check our work, aligning the protractor’s midpoint at the vertex of the angle.
- We then align the flat base line of the angle with the “0” mark on the protractor.
- We read the measurement off of the value that the line is pointing to, which reads 30°.
- We’re done!
Ready to give it a go?
-
Now, it’s your turn! We’re confident that you now know the basics to angles and angle measurement. Now, it’s time to practice.
Don’t be afraid to try and fail. It’s all part of the process! Remember that practice makes perfect, and know that you’re just a few sessions away from acing that next math exam. You’ve got this!
Practice Problems
Click to reveal the answer.
The answer is 180 degrees.

The answer is 90 degrees.
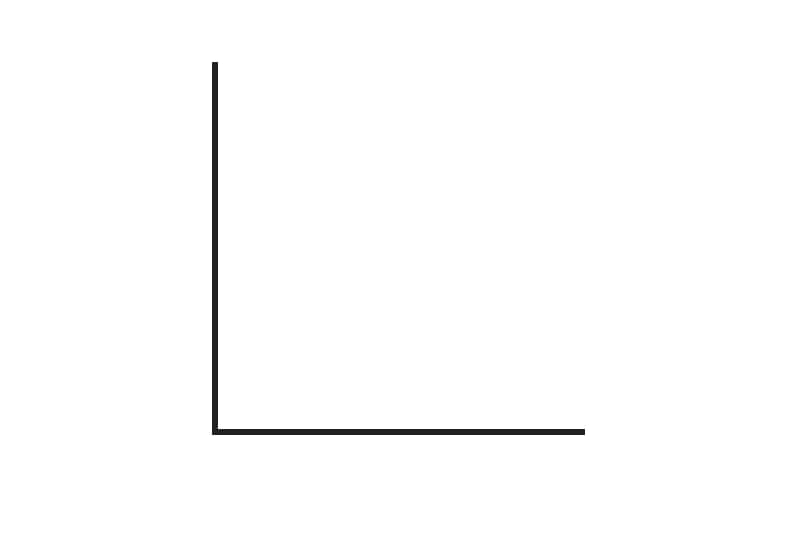
The answer is 15 degrees.
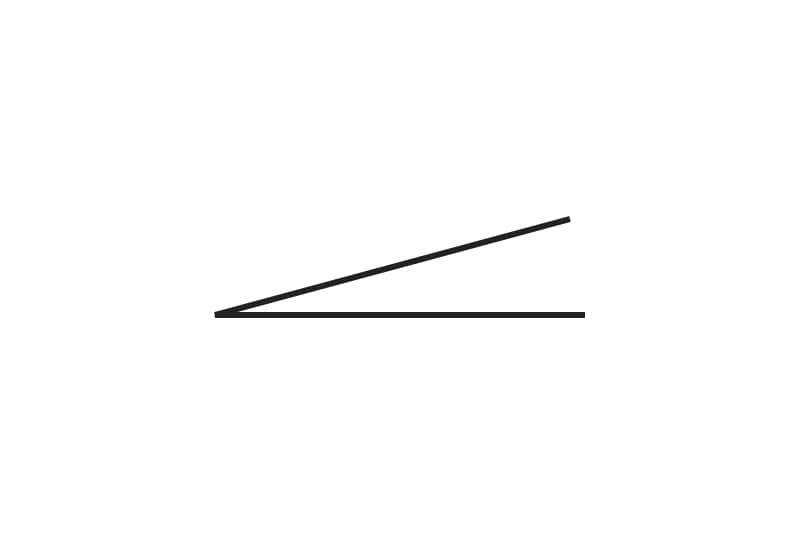
The answer is 150 degrees.
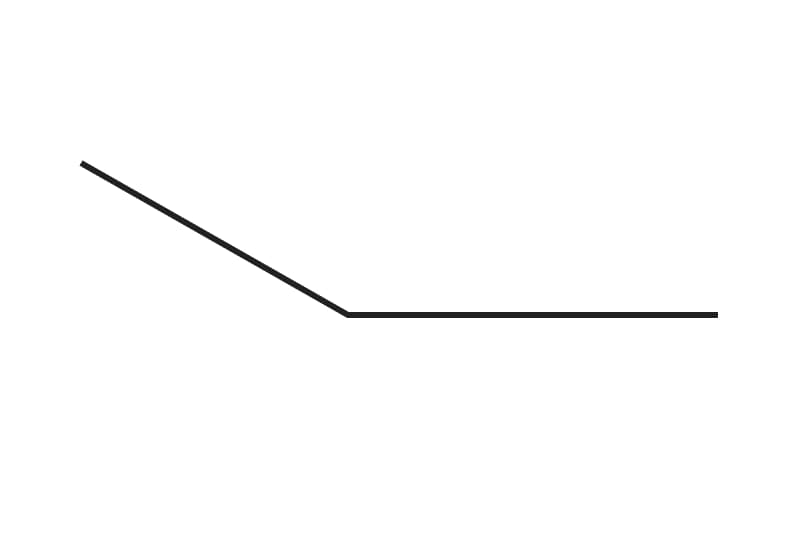
The answer is 70 degrees.
Parent Guide
-
1. The answer is 180 degrees. How did we get here?
- 1. Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
2. This angle appears to be a straight angle, which is an angle designation that can only be given to angles that have a measurement of 180°.
3. We check our work, aligning the protractor’s midpoint at the vertex of the angle.
4. We then align the flat base line of the angle with the “0” mark on the protractor.
5. We read the measurement off of the value that the line is pointing to, which reads 180°.
6. We’re done! -
2. The answer is 90 degrees. How did we get here?
- 1. Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
2. This angle appears to be a right angle, which is an angle designation that can only be given to angles that have a measurement of 90°.
3. We check our work, aligning the protractor’s midpoint at the vertex of the angle.
4. We then align the flat base line of the angle with the “0” mark on the protractor.
5. We read the measurement off of the value that the second vertical line is pointing to, which reads 90°.
6. We’re done! -
3. The answer is 15 degrees. How did we get here?
- 1. Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
2. This angle appears to be an acute angle, which is an angle designation that can only be given to angles that have a measurement of less than 90°.
3. We check our work, aligning the protractor’s midpoint at the vertex of the angle.
4. We then align the flat base line of the angle with the “0” mark on the protractor.
5. We read the measurement off of the value that the line is pointing to, which reads 15°.
6. We’re done! -
4. The answer is 150 degrees. How did we get here?
- 1. Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
2. This angle appears to be an obtuse angle, which is an angle designation that can only be given to angles that have a measurement of more than 90° but less than 180°.
3. We check our work, aligning the protractor’s midpoint at the vertex of the angle.
4. We then align the flat base line of the angle with the “0” mark on the protractor.
5. We read the measurement off of the value that the line is pointing to, which reads 150°.
6. We’re done! -
1. The answer is 70 degrees. How did we get here?
- 1. Before we begin measuring, we recall angle types. Does this angle match any specific angle (such as a right angle or a straight angle)?
2. This angle appears to be an acute angle, which is an angle designation that can only be given to angles that have a measurement of less than 90°.
3. We check our work, aligning the protractor’s midpoint at the vertex of the angle.
4. We then align the flat base line of the angle with the “0” mark on the protractor.
5. We read the measurement off of the value that the line is pointing to, which reads 70°.
6. We’re done!
FAQs about measuring angles
Use your protractor and place the midpoint at the vertex of your angle. Align the base line or ray with the “0” mark, and determine what class of angle it is (i.e., acute, obtuse, right, straight). Then, follow the second line of the angle and record where it is pointing to on the protractor.
Many find that the easiest way to measure angles is to use a protractor.
A right angle is an angle that is exactly 90 degrees.
A straight angle appears as a flat line and is an angle that is no more or no less than 180 degrees.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

