What are parallel lines?
Parallel lines are an important concept in geometry that we see everywhere we look in everyday life. Learn the definition of parallel lines and how we use them in math.

Author
Michelle Griczika
Published:
Oct 2024
Key takeaways
- • Parallel lines never intersect and are always the same distance apart.
- • Real-life examples of parallel lines are everywhere we look. Train tracks and the double yellow lines that separate traffic on the road are two examples.
- • A transversal line that intersects two parallel lines will form four, identical angles.
Parallel lines are an important concept in geometry that also have many real-world applications. They are lines that never intersect, no matter how far they are extended in either direction.
Here at DreamBox, we’re experts at making math easy. In this article, we’ll tell you everything you need to know about parallel lines, how to identify them, and how they are used in the real world.
What are parallel lines?
Parallel lines are two or more lines that are always the same distance apart and never intersect, even if they are extended infinitely in both directions.
They are always equidistant and run in the same direction, which means they have the same slope.
These lines are a fundamental in geometry and have many real-world applications. Don’t believe us? Parallel lines are used in architecture, engineering, navigation, and even sports.
Table of contents
Get more math practice with DreamBox!
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

What do parallel lines look like?
Parallel lines look like two straight lines that are always the same distance apart and never intersect, even if they are extended infinitely in both directions. They can be represented by drawing two straight lines side by side with an arrowhead at each end to indicate that they continue infinitely in both directions.
Parallel lines always have the same slope, which means that if you were to draw a perpendicular line to one of the parallel lines, it would intersect the other line at a right angle.
What is a transversal line?
Now that you know what a parallel line is, it’s helpful to know what a transversal is. This type of line intersects two or more other lines at different points. When a transversal intersects two parallel lines, it creates a set of angles like: corresponding angles, alternate interior angles, and alternate exterior angles.
Understanding the properties of transversal lines and the angles they create is essential to solving many geometry problems and applying these concepts in practical, real-life situations.
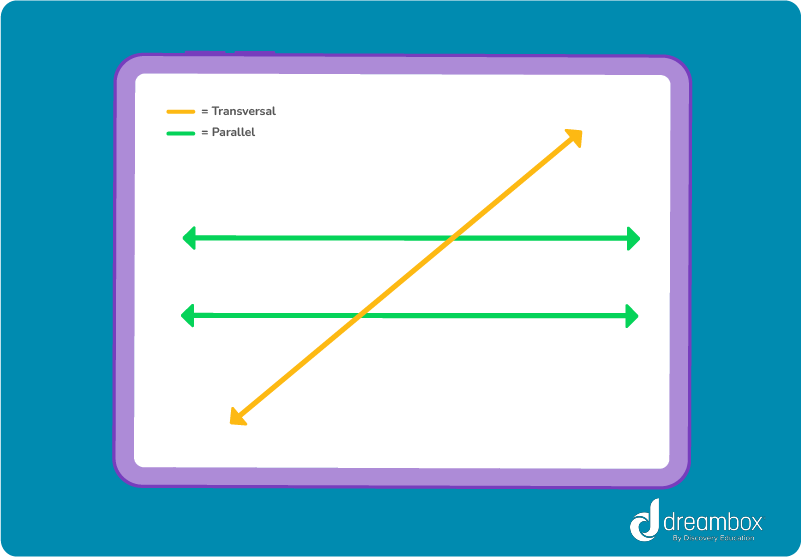
Properties of parallel lines
Parallel lines have several important properties that make them useful in geometry and real-world applications. Some of these properties include:
- Parallel lines are always straight
- Parallel lines have an equal distance from one another
- Parallel lines never intersect
- A transversal line that intersects two parallel lines will form four, identical angles
How to prove two lines are parallel
So what’s next? It’s easy to eyeball parallel lines, but you’ll want to know a way to prove it. To determine that two lines are parallel, you need to demonstrate that they have the same slope and never intersect, no matter how far they are extended in both directions. There are a few proven ways to do this.
Slope-intercept formula
One way to prove that two lines are parallel is by using the slope-intercept formula, which is y = mx + b. In this equation, m is the slope of the line and b is the y-intercept. If two lines have the same slope and different y-intercepts, then they are parallel.
Transversal theorem
Another way to prove that two lines are parallel is by using the transversal theorem, which states that if a transversal intersects two lines and the corresponding angles are congruent, then the lines are parallel.
Additionally, you can also use the alternate interior angles theorem, which states that if a transversal intersects two lines and the alternate interior angles are congruent, then the lines are parallel. These methods are all essential in proving that two lines are parallel and are frequently used in geometry and many other fields.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Examples of parallel lines in real life
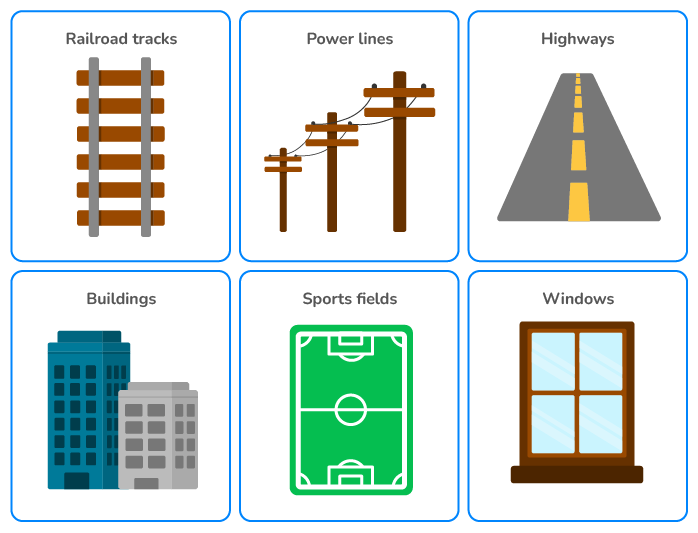
Look around, and see if you can notice any parallel lines. They’re all around us, every day. Here are a few examples:
- Railroad tracks: Railroad tracks are a classic example of parallel lines. The two tracks are always the same distance apart and never intersect, even though they may extend for miles in both directions.
- Power lines: Power lines that run along the side of the road are also parallel. They are always the same distance apart and never intersect, even if they extend for many miles.
- Highways: The lanes on a highway are parallel lines. They are always the same distance apart and run in the same direction.
- Buildings: The walls of buildings often have parallel lines. For example, the sides of a rectangular building are parallel lines, and the sides of a triangular building are also parallel.
- Sports fields: The lines on a soccer field, basketball court, or football field are all parallel.
- Windows: The frames of windows in a building are often parallel lines. They are always the same distance apart and never intersect.
These are just a few examples of parallel lines in real life. Parallel lines have many more uses and can be found in many other objects and structures around us.
Now that you know all about parallel lines, what do you want to learn about next? Math doesn’t have to be complicated, it can be fun. DreamBox can help students and parents build confidence and strengthen their skills across various topics. Interested?
FAQs about parallel lines
There are three different types of parallel lines, which include horizontal, diagonal, and vertical.
The opposite of parallel lines is intersecting lines. Intersecting lines are two lines that meet or cross at a single point. Unlike parallel lines, intersecting lines have different slopes, and they intersect at a specific point. Intersecting lines are also known as non-parallel lines, and they can form different angles depending on their intersection.
Different from parallel lines, intersecting lines are commonly found in nature and everyday objects, such as the intersection of roads, branches of trees, scissors, and the edges of geometric shapes.
The symbol for parallel lines is two vertical lines that are placed side by side, just like this: ∥. The symbol is used to indicate that two lines are parallel and will never meet or intersect, no matter how far they are extended in both directions.
If two lines have the same slope and different y-intercepts, then they are parallel. The equation for this is y = mx + b. For example, y = 2x + 1 and y = 2x + 5 represent two parallel lines.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


