What are Perpendicular Lines?
In this guide, learn all about perpendicular lines and how to identify them!

Author
Katie Wickliff
Published:
Oct 2024
Key takeaways
- • Perpendicular lines are two straight lines that meet or intersect at 90°.
- • The opposite of perpendicular lines are parallel lines. Unlike perpendicular lines, parallel lines never intersect.
- • The equation of a line that is perpendicular is y = mx + c.
What do television screens, postcards, and football goalposts have in common? They all meet at a specific angle to form perpendicular lines. So, what does “perpendicular” mean? In this article, we’ll answer that question and learn all about perpendicular lines, including how to draw them with different tools.
What are Perpendicular lines?
In mathematics, perpendicular lines are two straight lines that meet or intersect at 90°. This intersection is also called a right angle and is marked by a small square as shown in the figure below:
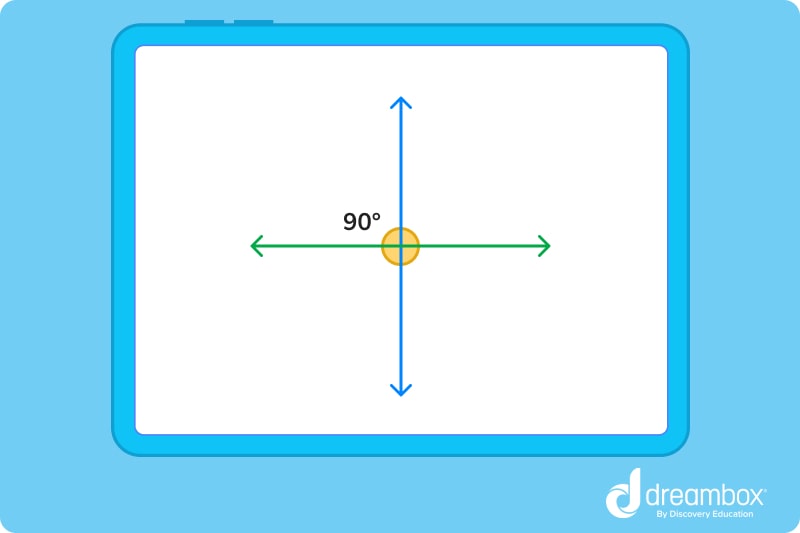
Perpendicular Definition and Origin
The definition of perpendicular is a straight line at an angle of 90° to a given line, plane, or surface. The word ‘perpendicular’ originated from the Latin word ‘perpendicularis,’ meaning a plumb line.
Table of contents
Get more math practice with DreamBox!
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

What do Perpendicular Lines Look Like?
Here are several perpendicular line examples:
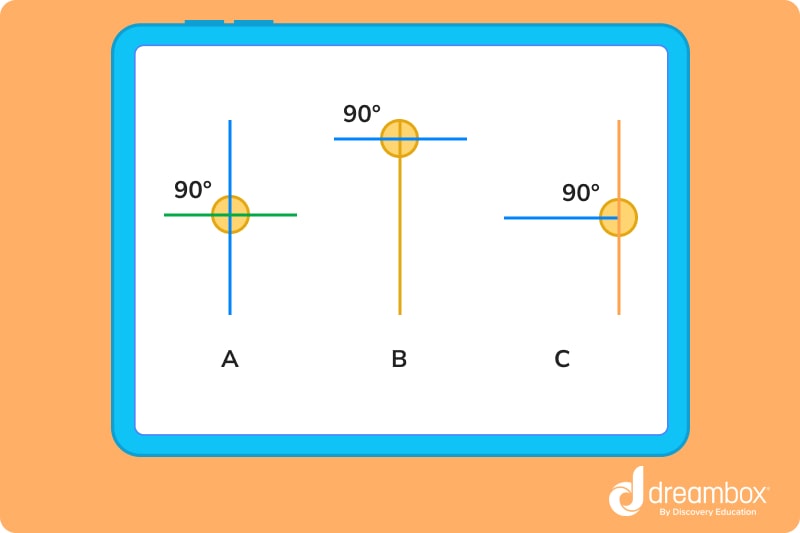
In the graphic above, you’ll notice that the angles meet or intersect at 90°.
All perpendicular lines intersect, but not all intersecting lines are perpendicular. Some lines intersect at different angles. To deepen your understanding, here are a few examples of lines that are NOT perpendicular:
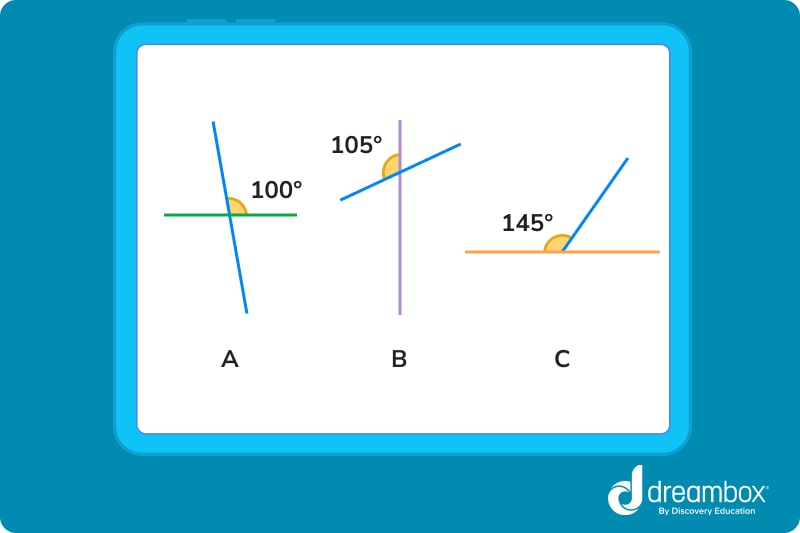
In this example, the lines form an obtuse angle (greater than 90°).
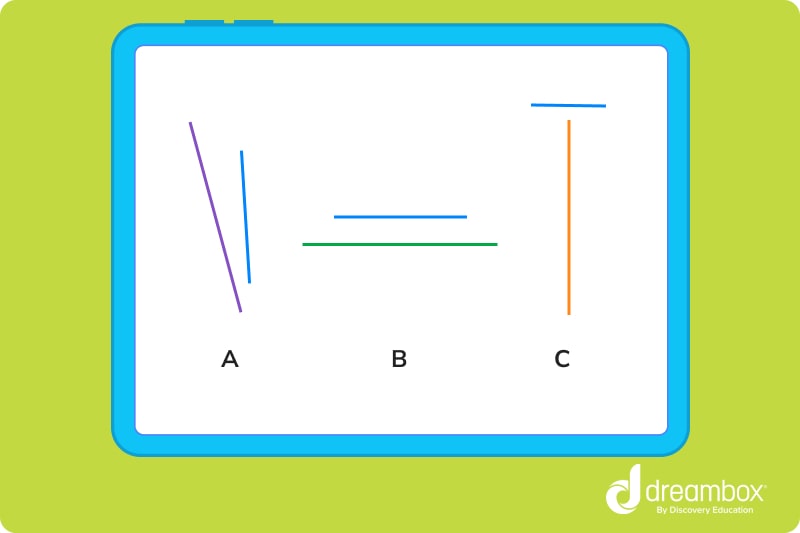
In this example, the lines do not meet or intersect, so they cannot be perpendicular.
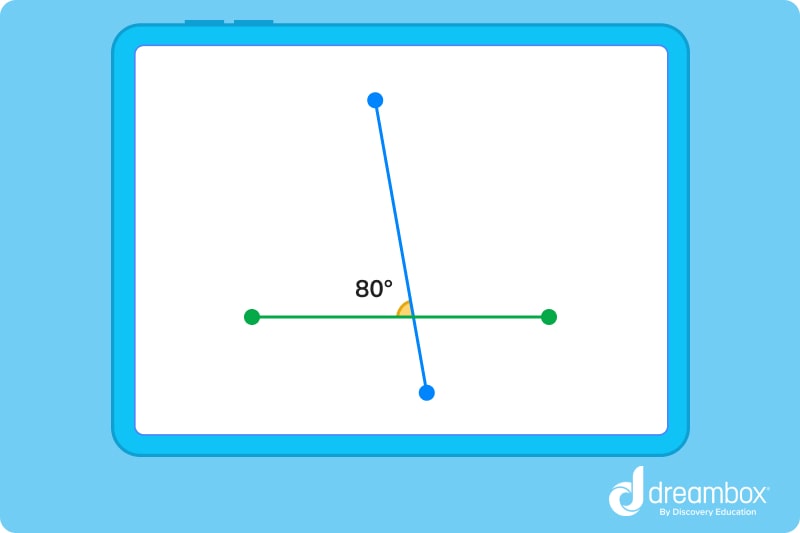
In this example, the lines form an acute angle (less than 90°).
How to Draw Perpendicular Lines
To create perpendicular lines, the angles must measure exactly 90°. It’s difficult to draw an exact right angle without tools. However, you can easily draw perpendicular line segments with a protractor or a compass.
A. Drawing Perpendicular Lines with a Protractor
Step 1: To draw perpendicular lines with a protractor, use a ruler to draw a straight horizontal line.
Step 2: Then, draw a dot somewhere on the horizontal line. For this example, let’s label the dot P.
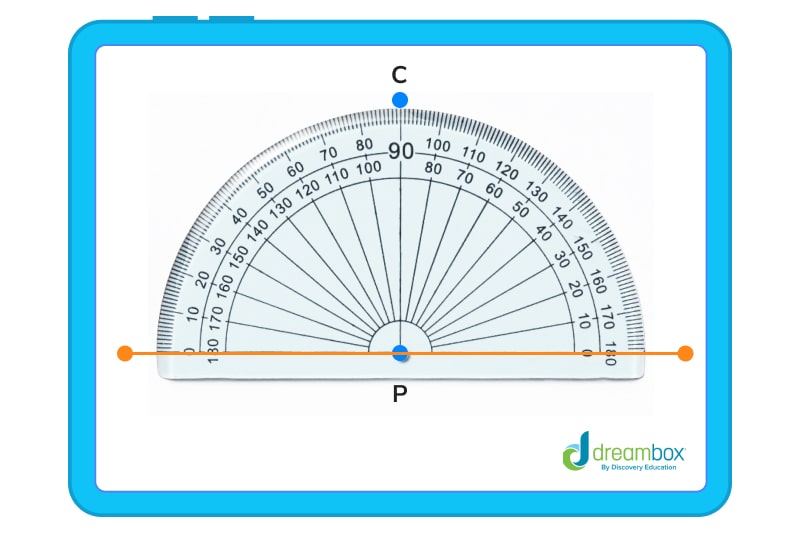
Step 3: Now, place the baseline of the protractor along the horizontal line with the center at P.
Step 4: Mark a point, C, at the 90 mark of the protractor, like this:
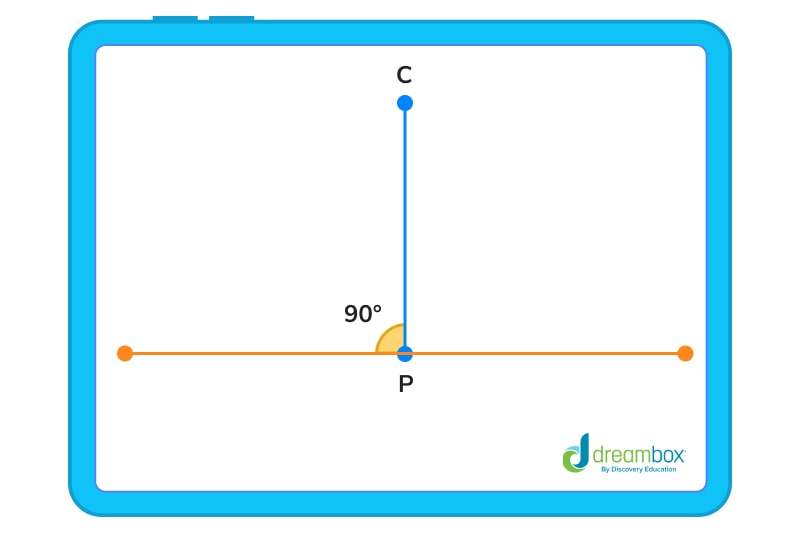
Step 5: Remove the protractor, and using your ruler or straight edge, draw a line that connects the points C and P.
B. Drawing Perpendicular Lines with a Compass
Another way to draw exact perpendicular lines is with a compass. In math, a compass is a drawing tool that allows you to create precise circles and arcs.
To draw perpendicular lines with a compass:
Step 1: First, use a ruler to draw a straight horizontal line.
Step 2: Then, draw a dot somewhere on the horizontal line.
Step 3: Put your compass point on the dot and draw a small circle around the dot. The size of the circle doesn’t matter, as long as it doesn’t take up more than half the length of your original line.
Step 4: Place your compass point on the part of the circle that touches the line. For this example, we labeled this point A.
Step 5: Open your compass wider and draw an arc above the circle.
Step 6: Place your compass point on the other part of the circle that touches the line. For this example, we labeled the point B.
Step 7: Again, open your compass wider and draw an arc above the circle that intersects with your first arc, like this:
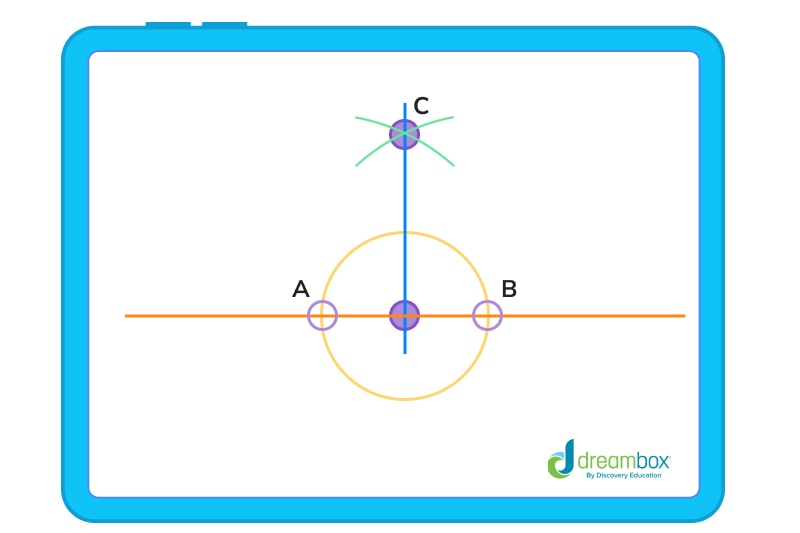
Step 8: Draw a dot where the arcs intersect. For the example above, we labeled the point C.
Step 9: Finally, taking your ruler or straight edge, draw a vertical line from point C down through your first horizontal line.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Properties of Perpendicular Lines
There are two main properties of perpendicular lines:
- Perpendicular lines always intersect at a right angle. A right angle always measures 90°.
- If one line has two perpendicular lines crossing it, those intersecting lines are parallel and never intersect with one another.
Perpendicular Versus Parallel Lines
Parallel lines are two straight lines in the same plane that never meet, no matter how long they stretch. Parallel lines can run vertically or horizontally. Real-world examples of parallel lines include lines on a sheet of notebook paper, the edges of a ruler, and railroad tracks.
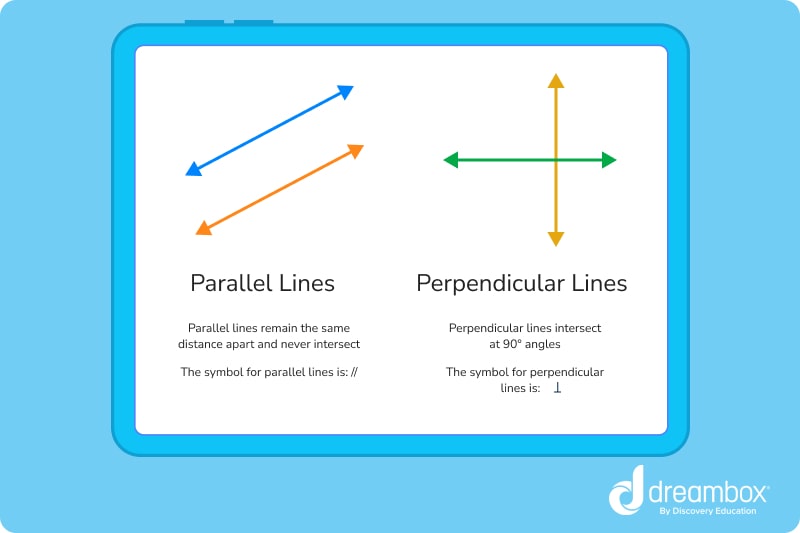
The table above highlights the main differences between perpendicular and parallel lines.
How to Prove Two Lines are Perpendicular
You can prove two lines are perpendicular in several ways. One common method to prove two lines are perpendicular is by using a protractor. Since you know that two lines are perpendicular if they meet at right angles, use your protractor to measure the angle.
Step 1: First, align the center marker of your protractor with the point where the two lines intersect, like this:
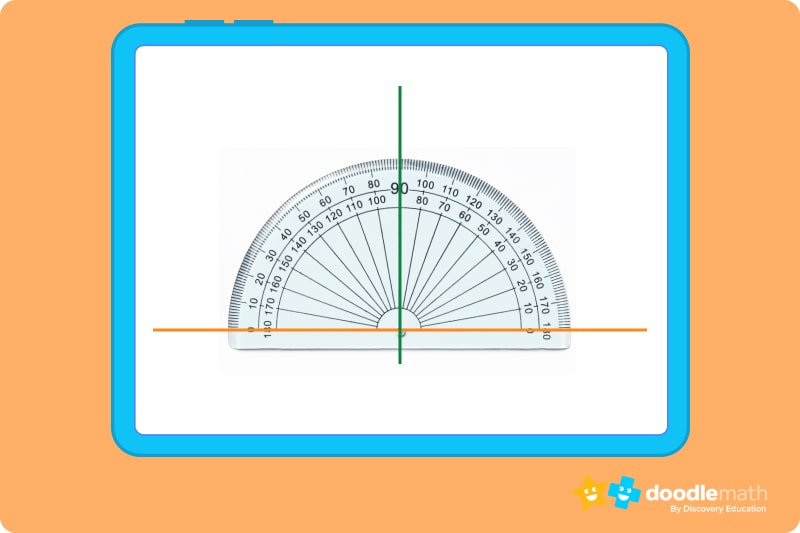
Make sure to have the bottom of your protractor line up with the horizontal line on your paper.
Step 2: Next, look at the vertical line and see what angle your protractor shows. If the protractor shows that the vertical line is at 90°, then your lines are perpendicular.
Examples of Perpendicular Lines in Real Life
Our world is full of perpendicular lines. If you look around your home, school, or playground, you’ll find several examples of perpendicular lines. Some of the most common are:
- Textbook corners
- Endzone of a football field
- Hands of a clock at certain times, such as 3 o’clock or 9 o’clock
- Adjacent edges of a picture frame
- Laptop corners
- Flag corners
- Lamppost and sidewalk

FAQs about perpendicular lines
Perpendicular means a line at a right angle to another line or plane.
In geometry, the opposite of perpendicular lines is parallel lines. Unlike perpendicular lines, parallel lines never intersect.
The symbol for perpendicular lines is: ⊥.
The equation of a line that is perpendicular is y = mx + c
You can use this formula to identify perpendicular lines if you know their coordinates.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


