Menu
Thousands of years ago, a Greek philosopher named Pythagoras discovered a formula to help us solve the lengths of a right triangle. It’s called the Pythagorean theorem — let’s learn more!
Author
Lucy Hart
Last Updated
July 12, 2023
Thousands of years ago, a Greek philosopher named Pythagoras discovered a formula to help us solve the lengths of a right triangle. It’s called the Pythagorean theorem — let’s learn more!
Author
Lucy Hart
Last Updated
July 12, 2023
Thousands of years ago, a Greek philosopher named Pythagoras discovered a formula to help us solve the lengths of a right triangle. It’s called the Pythagorean theorem — let’s learn more!
Author
Lucy Hart
Last Updated
July 12, 2023
Key takeaways
Over 2,000 years ago, a Greek philosopher called Pythagoras created a very famous theorem about triangles. It lets you work out the length of any side in a right-angled triangle!
The Pythagorean theorem states:
“In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the two shorter sides.”
This may sound a bit complicated, but it makes a lot more sense when we look at what it’s saying in the form of a picture:
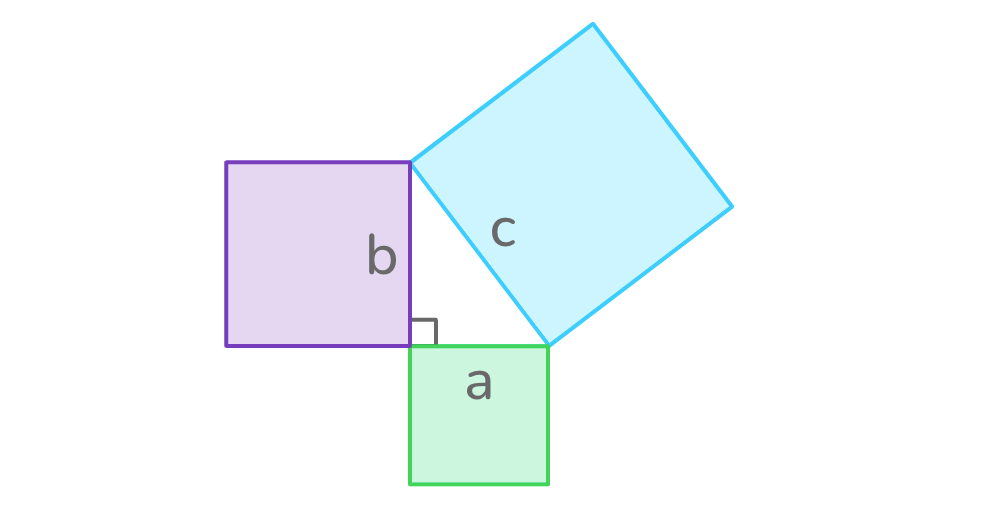
When squares are drawn along each side in a right triangle, the total area of the two smaller squares (those along the shortest sides, a and b) is the same as the area of the largest square (the square along the longest side, c).
By working out the area of each square, we can find the length of any side in a right triangle. And luckily, Pythagoras created a handy formula to help us do this!
Unlock unlimited math questions
Put your skills to the test with fun exercises + math games that are proven to boost ability!
Try DoodleMath for Free!
Select a grade
The formula for Pythagoras’ theorem is a² + b² = c².
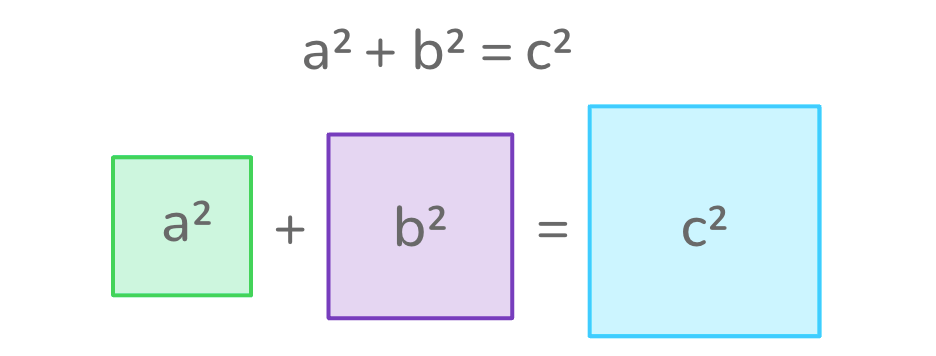
In this equation, “C” represents the longest side of a right triangle, called the hypotenuse. “A” and “B” represent the other two sides of the triangle.
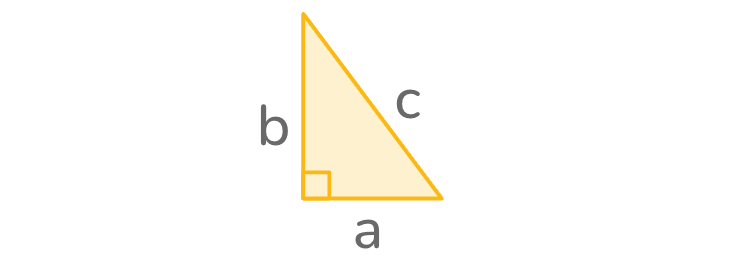
To use the Pythagorean theorem formula, we need to know the length of any two sides in a right triangle. We can then rearrange the formula to find the side we’re looking for.
So, if we take the formula:
a² + b² = c²
We can rearrange it to help us find the length we’re missing:
This may sound complicated, but don’t worry! It’s easy to use once you know how. Let’s take a look at some examples.
Now that we know the Pythagorean theorem formula is, let’s talk about what we can use it for. The Pythagorean theorem can be used to solve for the hypotenuse or the shorter sides of a right triangle.
If we don’t know the length of the hypotenuse of a right triangle (aka the longest side), we can work it out using Pythagoras’ theorem. The hypotenuse is represented by c in the Pythagorean theorem formula: a² + b² = c². By plugging in the given values of Side A and Side B, we can solve for the hypotenuse — Side C!
Let’s try an example!
Looking at the picture below, solve for Side C.
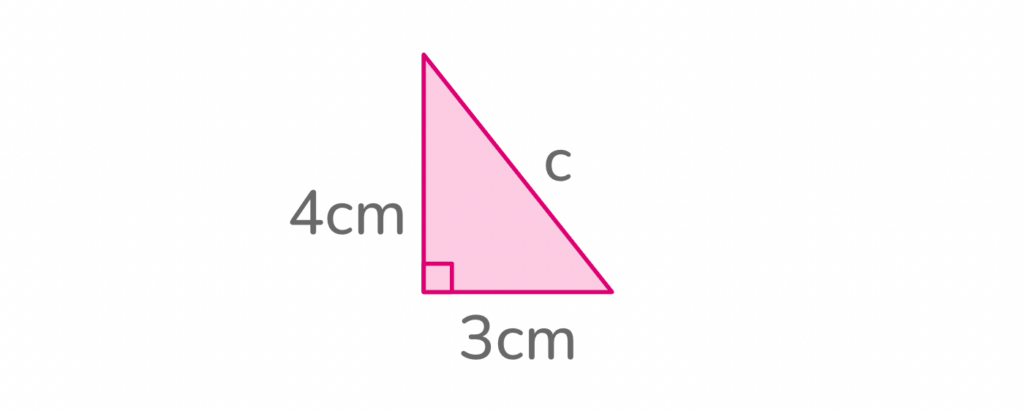
To start, we can flip the Pythagorean theorem equation to make it easier to read:
a² + b² = c² becomes c² = a² + b²
Next, plug the values of Side A and Side B into the equation since they are given. Side A = 4cm and Side B = 3cm. This gives us:
c² = 4² + 3²
Square Sides A and B to get:
c² = 16 + 9
Add 16 and 9 solve for a²:
c² = 25
Now we’re in the final stretch. We just need to find the square root of 25 to find the length of the hypotenuse (Side C)!
c² = √25
Therefore, the length of Side C = 5cm.
We can also use Pythagoras’ theorem when we don’t know the length of one of the shorter sides of a right triangle.
We can rearrange the formula to help us find the side we don’t know. For example:
Let’s practice! In the example below, solve for Side A.
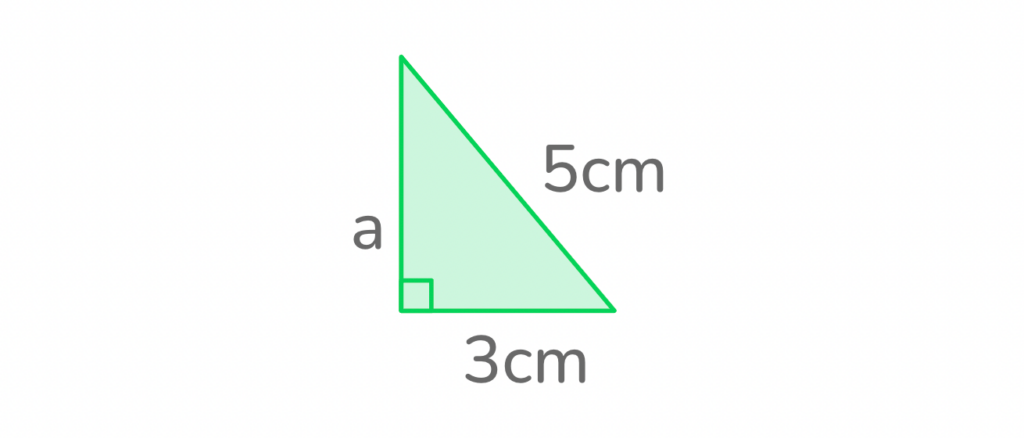
To work out the length of Side A, start by rearranging the formula to become:
a² = c² – b²
Next, plug in the values of Side C and Side B. (Remember: Side C is the hypotenuse!)
a² = 5² – 3²
Square Sides B and C to get:
a² = 25 – 9
Subtract 9 from 25 to solve for a²:
a² = 16
Now we’re nearly there! If we find the square root of 16, we’ll have our answer.
a = √16
Therefore, Side A = 4cm.
Want to learn more about the Pythagorean theorem? DoodleMath is an award-winning math app that’s proven to double a child’s rate of progression with just 10 minutes of use a day!
Filled with fun, interactive questions aligned to state standards, Doodle creates a unique work program tailored to each child’s needs, boosting their confidence and skills in math. Try it free today!
Ready to look at some more examples or have a go at using the theorem yourself? Take a look at the following practice problems with answers that follow!
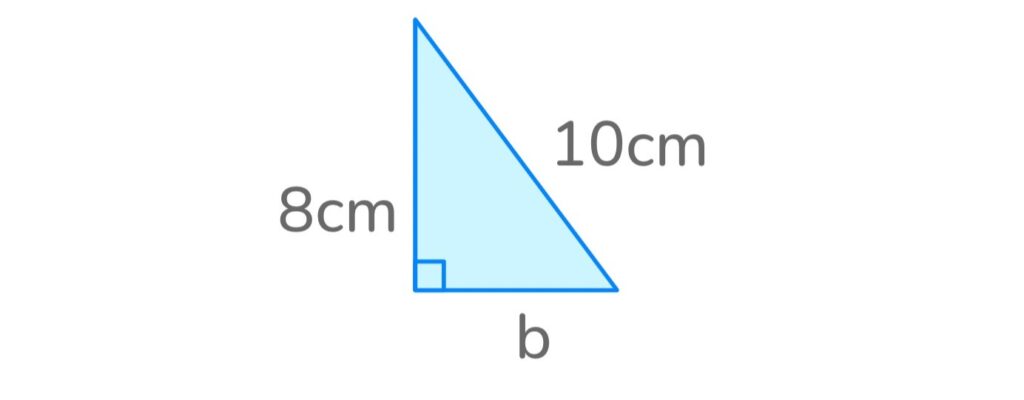
1. Find the length of b
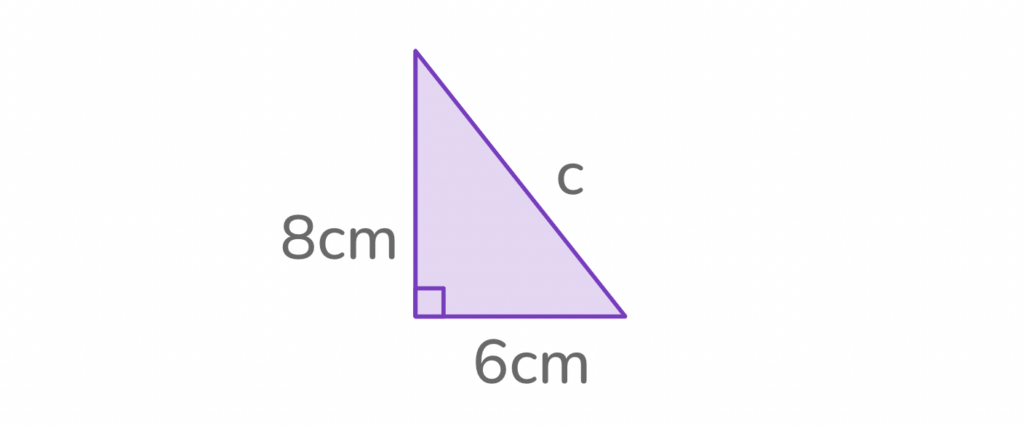
2. Find the length of C
Filled with interactive exercises, educational math games, and virtual rewards, the DoodleMath app brings learning to life like never before! To more practice geometry like the Pythagorean theorem in an interactive way, sign up for a free trial to give it a go!
Parents, sign up for a free subscription to the DoodleMath app and see your child become a math wizard!
Answer Sheet
Question 1
Answer: 6cm
Therefore, b = 6cm.
Question 2
Answer: 10cm
Therefore, c = 10cm.
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
