What Is the Least Common Multiple?
Read on to understand how to find the least common multiple in easy-to-understand terms.

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- It’s all in the name – The least common multiple (LCM) of two numbers is the smallest multiple you can find for both numbers.
- You’ve got options to find the LCM – From listing out multiples the long way or by factoring, you’ve got plenty of options to fit your math skills.
- LCM has many applications – The LCM, of course, factors into other math problems, but you’ll see LCM used to break people into groups, organize complex data, and even make some traffic lights work!
Math, despite how intimidating it may seem at first, is really just about finding commonalities. Multiples and factors go a long way to help you understand how different numbers are related and how you can predict their behaviors reliably.
The least common multiple (LCM) is just one of the ways mathematicians and everyday people understand the relationships between numbers. By figuring out these connections, you can unlock the many ways numbers work with one another.
What is the LCM?
To understand the least common multiple, you need to remember what a multiple is. As you may have learned before, a multiple of a number is the product you get when you multiply that number by any other number. If you want to find the multiples of 3, you would simply go down the line 1, 2, 3, 4, and so on, multiplying 3 by each number to find the products. That means that the multiples of 3 are 3, 6, 9, 12 and on.
For LCM, though, you fortunately just need to find the smallest multiple that two numbers share. For example, the LCM of 3 and 5 is 15. The multiples of 3 are 3, 6, 9, 12, 15, 18. And the multiples of 5 are 5, 10, 15, 20… 15 is the lowest number both of those lists have in common, so 15 is the LCM of 3 and 5.
Table of contents
Access more math practice with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

How to find the LCM
You’ve got a few options when you sit down to find the LCM of two numbers:
- Listing multiples
- Dividing prime numbers
- Prime factorization
- Greatest common factor
Some options are very simple, but they take a long time. Others are much quicker, but they do require you to understand factoring. Like with most math concepts, as your skills and understanding grow, the quicker and more confident you’ll become. Start with the simple long way and gradually work your way to the more complex and quicker methods.
Listing multiples
The simplest way to find the least common multiple of two numbers is to just list out the multiples of those numbers and look for the lowest number both lists share. This may take the longest of all the methods, but all you need to know is how to multiply to figure this one out.
Let’s play it out, and see how this is done. You want to find the LCM of 4 and 5.
Start by making three rows on your paper, one for the numbers you will multiply by (the multipliers: 1, 2, 3, and so on), one for multiples of 4, and one for the multiples of 5.
Once you have the table planned out, find the multiples of both numbers and fill in the table one multiplier at a time. Once you find a product that both lists share, you can stop. That will be your LCM.

After all that math, you can see that the lowest number that both lists share is 20. That means your LCM is 20! Let’s look at one more example. How about the LCM of 7 and 13?
As before, write out your table and start figuring out the multiples of 7 and 13 — up to the multiplier 7. This is because 7 x 13 will be a common multiple for sure.
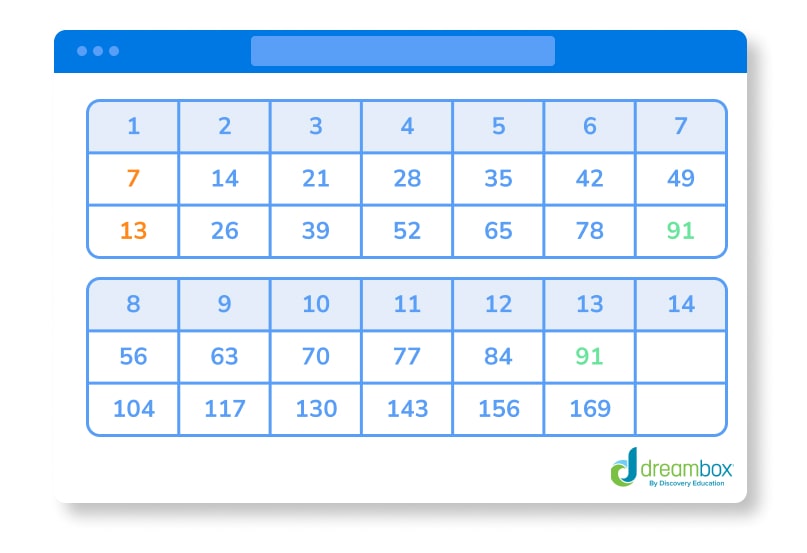
Dividing prime numbers
Listing multiples can be time-consuming, but, fortunately, there are much faster methods. The next option is quicker, but you do need to know what prime numbers are. Prime numbers are numbers that can be divided evenly only by 1 and the number itself. For instance, 13 is a prime number because you can only divide 13 evenly by 1 and 13..
As you will see in a moment, these prime numbers can come in handy when trying to find the LCM between two numbers.
Put together a table with prime numbers in the left column and the two numbers you are trying to find the LCM for on the right separated by a comma or a line. Start dividing each number by the smallest prime number you can, moving on to the next highest when you need to. If one of the two numbers cannot be evenly divided by the prime number, keep it the same and move on down the line until you get 1 for both numbers. This sounds complicated! Don’t worry– it’s easier to see this in action.
Let’s use this method to find the LCM of 12 and 20.

Now that you have a row with two ones, go through the prime numbers on the left and multiply them together. The product is your LCM.
2 x 2 x 3 x 5 = 60, so 60 is the LCM of 12 and 20
Prime factorization
Prime factorization is a slightly faster version of the last option. You will do this by factoring both numbers you are trying to find the LCM of down to the prime factors.
Let’s go with 24 and 44.
To find the prime factorization of 24, begin by finding two factors that multiply to give you 24. Let’s say we use 8 x 3. 3 is a prime number, so we don’t need to break that one down any more. 8 is a composite number, so we need to break it down into two factors again. This time, we can use 2 x 4. 2 is a prime number, so we can set it aside. 4 is composite, so we break it down again into 2 x 2. Now, we have all prime numbers as factors of 24.
So, the prime factorization of 24 is 2 x 2 x 2 x 3, which can also be expressed as 2³ 𝑥 3.
Use this same method to find that the prime factors of 44 are 22, 2, and 11, which can be expressed as 2² and 11. You can start by dividing 44 by 2, which will get you 22 and 2 as factors. 2 is prime, so you are done with that one. 22 can be divided further into 11 and 2. Both of those are prime, so you are left with 2, 2, and 11 as factors.
Now, look at all the factors you got for both numbers together. We have 2³ 𝑥 3 for one, and 2² 𝑥 11 for the other. To find the LCM, we will multiply the factors, leaving out any that overlap. For this example, 3 and 11 don’t have any overlap, so we will use them both. For the 2’s, the overlap is 2^2, so we will only use the 2^3.
You now have 2³, 3, and 11 set aside. Now you multiple those together to find the LCM.
2³ x 3 x 11 = 264. That’s your LCM.
Greatest common factor
If you can find the greatest common factor (or highest common factor) of two numbers, you can easily find the lowest common factor. You can use the formula: LCM = the product of two numbers ÷ the GCF.
If you need help with finding the GCF, make sure to check out our lesson, but, in short, you find the greatest common factor of two numbers by factoring both numbers and looking for the largest number in common in both factor trees.
Let’s try this out with 24 and 36.
12 is the greatest common factor of both 24 and 36. 12 x 2 = 24 and 12 x 3 = 36.
Now, according to our formula, you multiply 24 and 36 together and divide the product by 12, the GCF.
(24 x 36) ÷ 12 = 72. That means the LCM of 24 and 36 is 72.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Let's Practice Together!
1. Find the LCM of 8 and 20 by listing multiples.

The LCM is 40.
2. Find the LCM of 9 and 21 by dividing prime numbers.

3 x 3 x 7 = 63, so that is the LCM.
3. Find the LCM of 25 and 42 with prime factorization.
The prime factors of 25 are 5 and 5, expressed as 5².
The prime factors of 42 are 2, 3, and 7.
Multiply 5², 2, 3, and 7 together to get 1050. That’s the LCM.
4. Find the LCM of 32 and 80 using GCF.
The GCF of both 32 and 80 is 16.
(32 x 80) ÷ 16 = 160. 160 is the LCM.
Ready to give it a go?
- Time to try this out on your own. Remember to look back at the lesson for guidance. If the math doesn’t seem to be working out, retrace your steps, and see where you maybe missed a step or miscalculated.
Practice Problems
Click to reveal the answer.
The answer is 36.
The answer is 150.
The answer is 2340.
The answer is 2550.
Parent Guide
-
1. 24. How did we get here?
- 1. List out the multiples of each number until you find a number that is on both lists. Remember, you only need to go through multiples up to the product of the two numbers.
2. The multiples of 6 are 6, 12, 18, 24, 30, 36, 42, and 48.
3. The multiples of 8 are 8, 16, 24, 32, 40, and 48.
4. The least common multiple of 6 and 8 is 24. -
2. 36. How did we get here?
- 1. Start dividing each number by prime numbers that produce whole number quotients.
2. Now multiply all the prime numbers together.
3. 2 x 2 x 3 x 3 = 36
4. 36 is the LCM

-
3. 150. How did we get here?
- 1. Find the prime factors of each number and express any multiples as exponents.
2. The prime factors of 15 are 3 and 5
3. The prime factors of 50 are 2 and 52
4. Of the factors with the same base number, pick the one with the highest exponent value. This gives us 2, 3, and 52.
5. Multiple them together to get 150, the LCM. -
4. 2,340. How did we get here?
- 1. Find the factors of both numbers.
2. The factors of 52 are 1, 2, 4, 13, 26, and 52
3. The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90
4. The GCF is just 2. Now, plug that into the formula.
5. (52 x 90) ÷ 2 = 2340. -
5. 2,550. How did we get here?
- 1. Since these numbers are larger, it’s best to avoid the listing multiples option.
2. 75 and 102 are simple to factor, so either the prime number method or the GCF method may be the best option.
3. Let’s use the GCF method here. You need to first factor out both numbers.
4. 75 can be divided by 3 to get 25. 3 is prime, and 25 can be divided further into 5 and 5. 5 is also prime, so you are done there.
5. 102 can be divided into 2 and 51. 2 is prime, so now you divide 51. 51 can be split into 17 and 3, both of which are prime.
6. That means the GCF of 75 and 102 is 3.
7. Now we follow the formula: (75 x 102) ÷ 3 = 2550
FAQs about least common multiple
LCM stands for Least Common Multiple. It is the smallest number that is a multiple of two or more numbers.
To find the LCM, you can list out the multiples of each number until you find a number that is on both lists. You can also use division, prime factorization, and greatest common multiple to find the LCM.
LCM can be used to solve problems involving time, money, and distance. For example, you can use LCM to find the least common number of hours that two people can hang out or the least common amount of money that two people can pitch in for dinner.
Some common mistakes people make when finding LCM include:
- Accidentally skipping a multiple when listing
- Not using all the prime factors of a number
- Making careless errors when multiplying numbers.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


