How to Do Long Multiplication
Multiplying large numbers can be easy if we are willing to break the problem into parts!

Author
Amber Watkins
Published:
Oct 2024
Key takeaways
- • Long multiplication makes multiplying large numbers easy by helping students multiply numbers in parts.
- • Mastering long multiplication takes practice, but it is a skill your child will always need in their math education. For more practice, see our math app for kids.
So, you’ve made it to the fourth grade. And the numbers keep growing in size. What are we going to do? Well, there’s a silly saying… “How to eat an elephant?… One bite at a time!” It teaches us that if you have a large task, the best way to do it is in parts.
The same can be true with multiplication. When we are given large numbers to multiply, instead of trying to do the problem all at once in our heads, we can multiply those numbers in parts.
When we multiply large numbers in parts, then add those parts together, it is called long multiplication.
What is long multiplication?
Long multiplication is the steps you follow to multiply larger numbers in an easy way. Long multiplication allows you to find partial answers and add them together to find the final product.
For example, instead of multiplying the numbers 64 x 32 as they are, you can break up the number 32 into two parts: 30 and 2, then multiply those parts by 64. It would look like this:
(64 x 2) + (64 x 30)
128 + 1,920
You would get a total of 2,048.
Multiplying in parts, and then adding the products together makes multiplying large numbers easy!
How to set up a long multiplication problem?
When doing long multiplication problems in a column method, you will line up the numbers you are multiplying in columns.
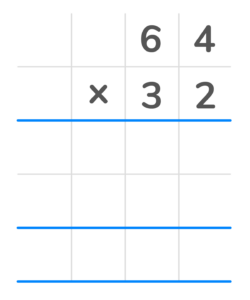
For example, how do we set up the problem 64 x 32 using the column method?
- The number 62 would be written above the number 32. The equal sign will be represented with a line underneath.
- You will also have two or more rows beneath. This is where you write the partial products. The first partial product is written in the first row, the second partial product is written in the second row, and so on.
- After adding the partial products, the final answer is written on the bottom row.
Let’s keep this in mind when reviewing the steps for how to do long multiplication.
Long Multiplication Steps- Column Method
Let’s learn the Long Multiplication Steps using the Column method as we solve the following problem:
What is 33 x 21?
1. Line up the numbers in a column format.
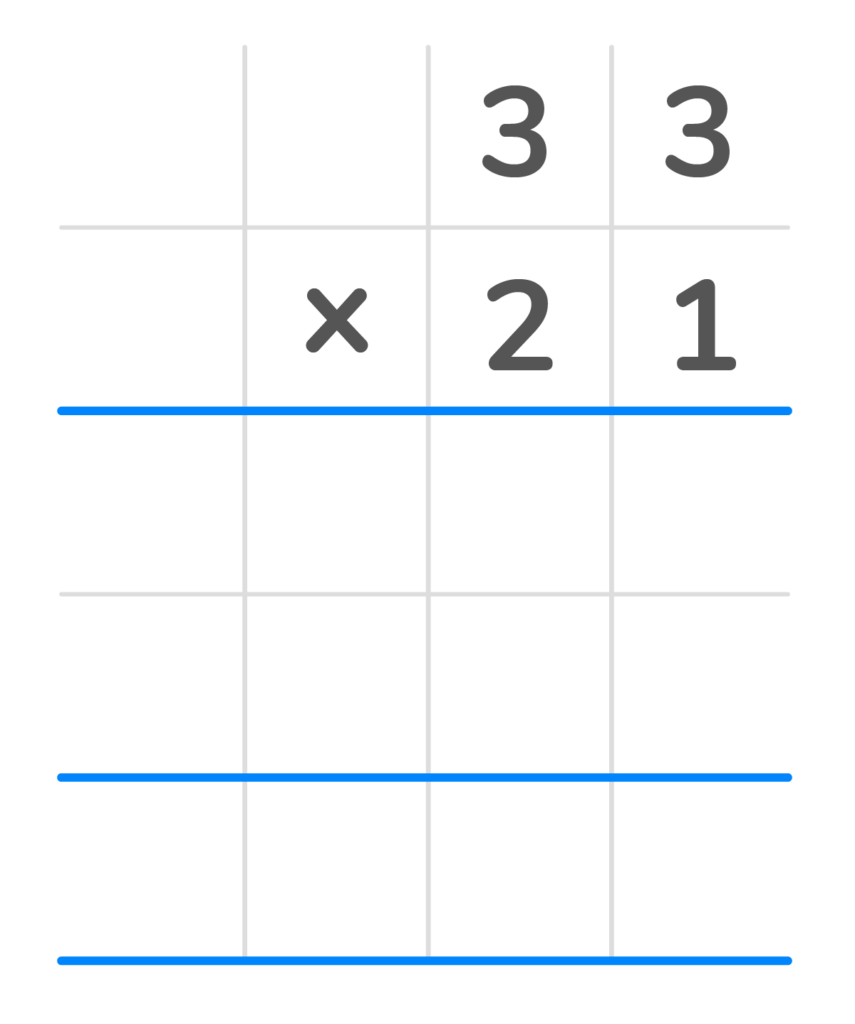
2. Multiply each top digit by the last digit in the bottom number. Place each answer in the first row from right to left. You should have the number 33 in the first product row.
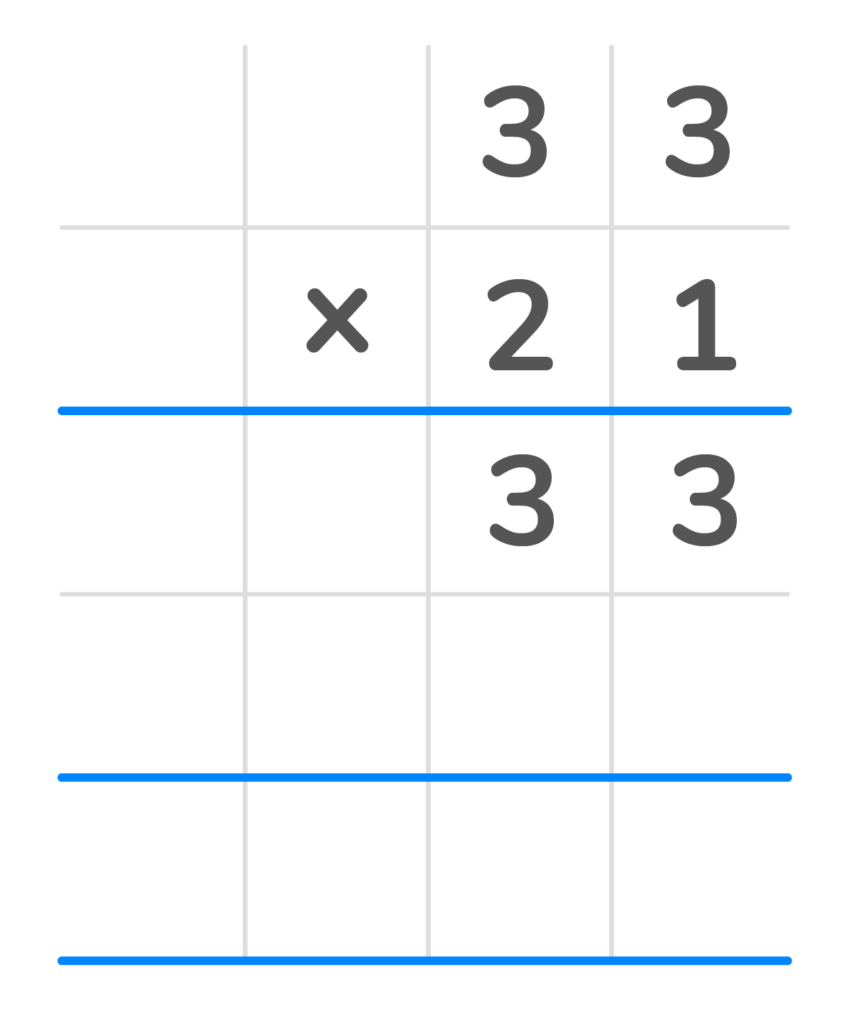
3. Once each of the top digits is multiplied by that number, cross it off.
4. Next add a zero as a place value holder in the second row to represent already multiplying by the digit in that place value.
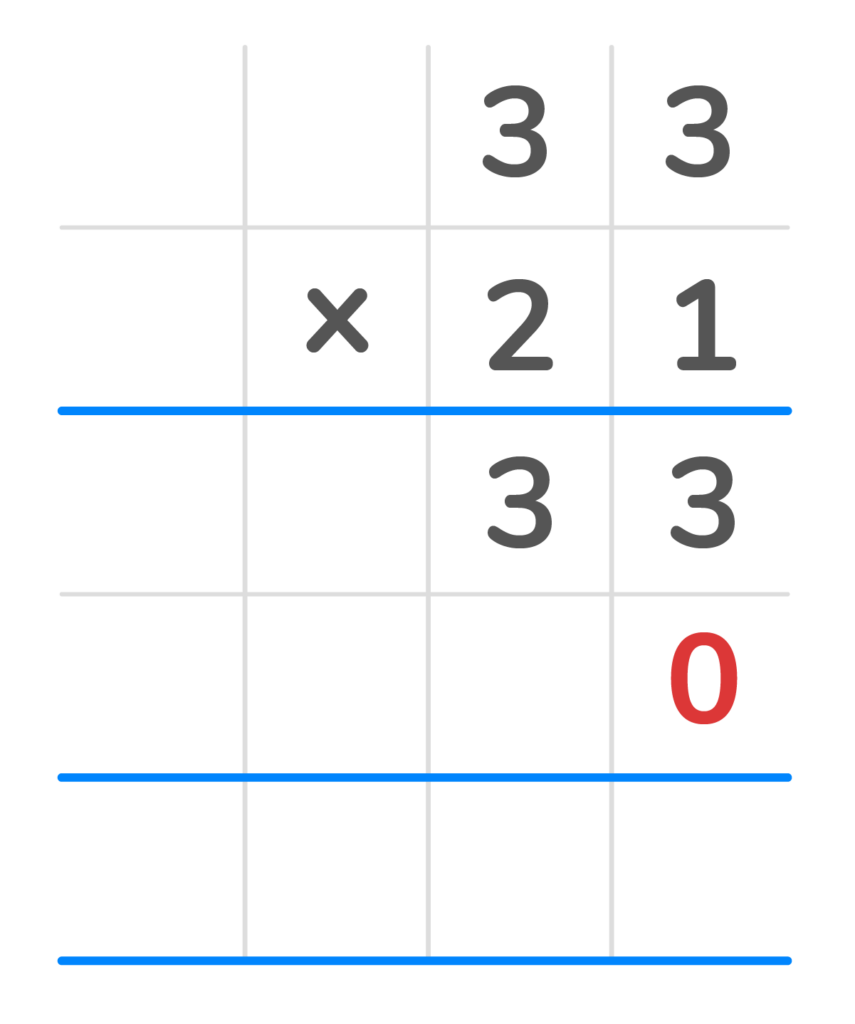
5. Multiply each top digit by the first digit in the bottom number. You will have the number 660 in the second partial product row.
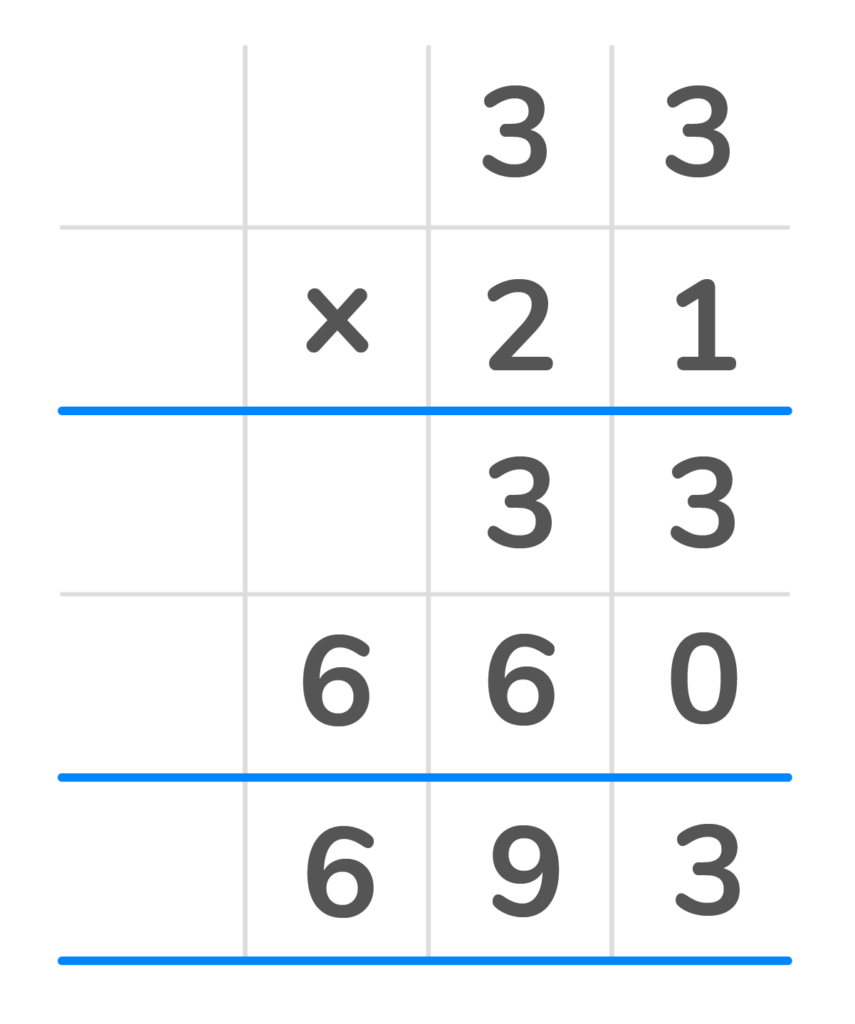
6. Finally add the two products 31 and 660 to get the final answer of 693.
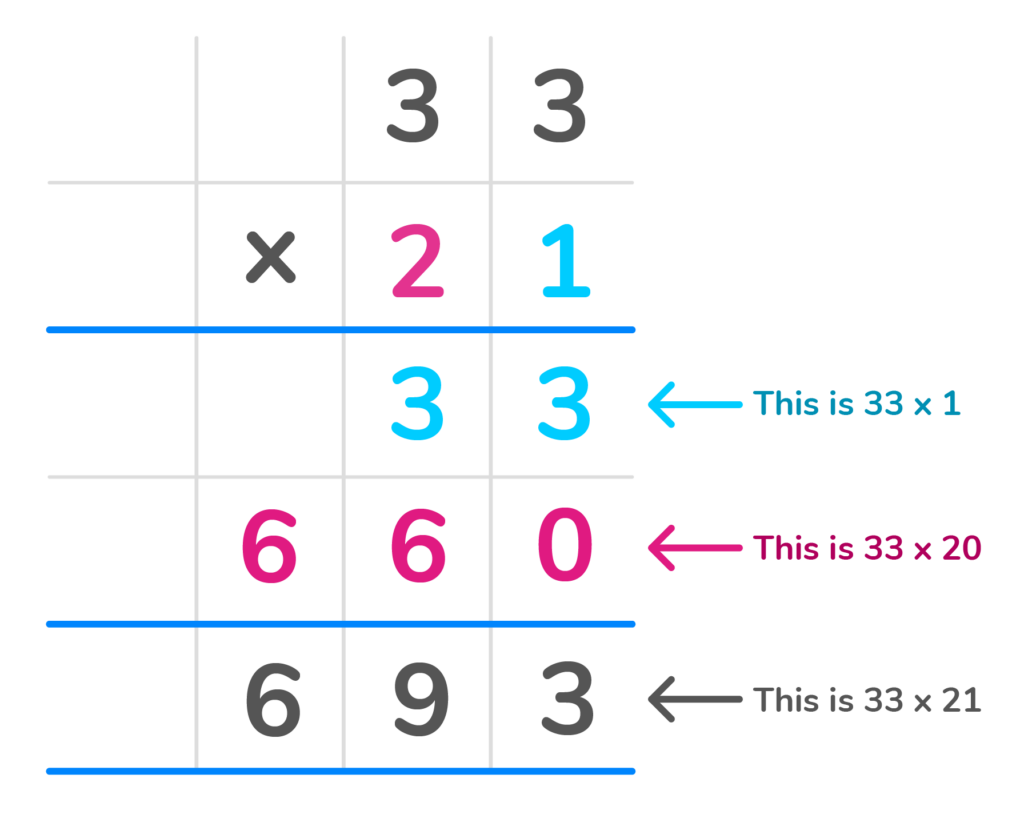
Table of contents
Practice more multiplication with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Carry-over Rule while doing Long Multiplication
If you multiply two digits and the answer is in the double digits, the carry-over rule says you must write the second digit in the partial product line, and the first digit above the next number you will need to multiply. That way it carries over.
Let’s see how these long multiplication steps and the carry-over rule work

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Long Multiplication Steps - Horizontal Method
Did you know there are two ways to do long multiplication: using the Column method or the Horizontal method? The horizontal method allows us to break up the second number in parts and multiply those parts by the first number.
Let’s learn how to do long multiplication with the horizontal method. Let’s look at this example.
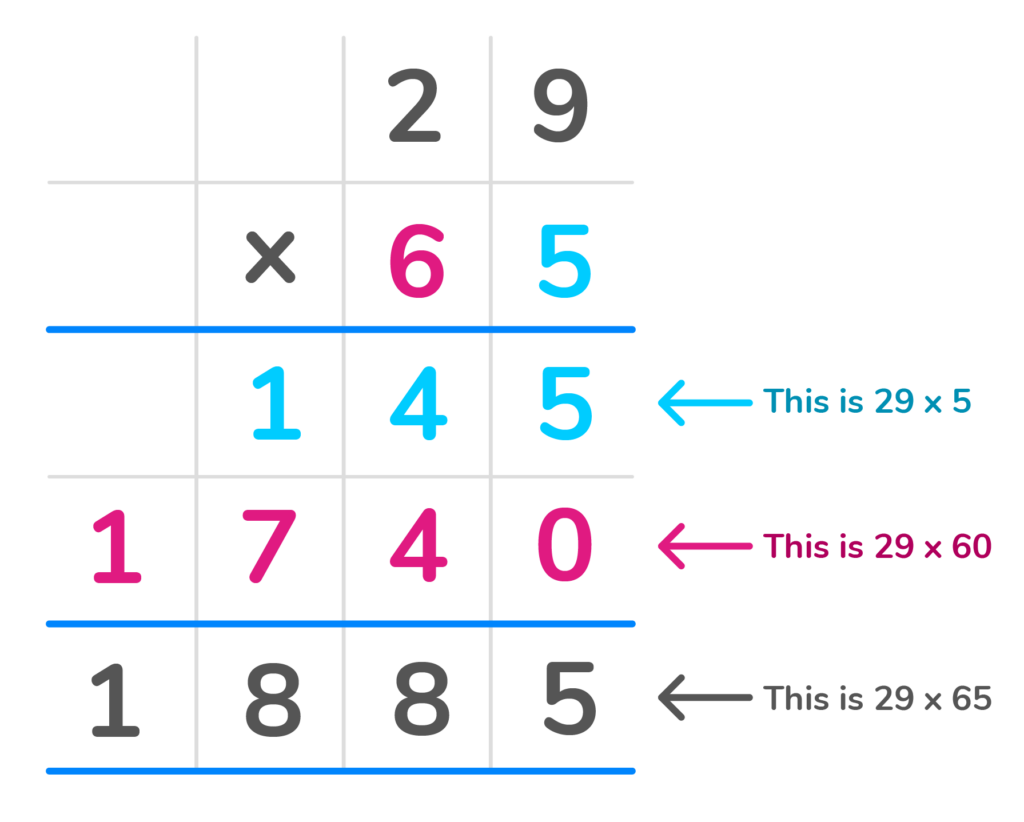
How to multiply 43 x 65 in the horizontal method?
1. Write the second number 65 in Expanded form. Those two numbers will be the parts we multiply the first number 43 by.
65 in Expanded form is 60 + 5.
2. Begin by multiplying 43 by the first part, 60. This can be done by multiplying 43 x 6, then adding a zero to the answer.
43 x 6 is 258.
Then add a zero, so it would be 2580.
3. Next we will multiply 43 by the second part 5.
43 x 5 is 215.
4. Finally, we add the two partial products together to get the final answer.
2580 + 215 is 2,795.
Practice Problems
Click on the boxes below to see the answers!
- Write 72 and 24 in columns.
- Multiply 2 x 4 and 7 x 4 and write the answers in the first row.
- Cross off the 4 and add a zero placeholder in the second row.
- Multiply 2 x 2 and 7 x 2 and write the answers in the second row.
- Add both columns together to get 1,728.
- Write 48 and 62 in columns.
- Multiply 8 x 2 and 4 x 2 and write the answers in the first row.
- Cross off the 2 and add a zero placeholder in the second row.
- Multiply 8 x 6 and 4 x 6 and write the answers in the second row.
- Add both columns together to get 2,976
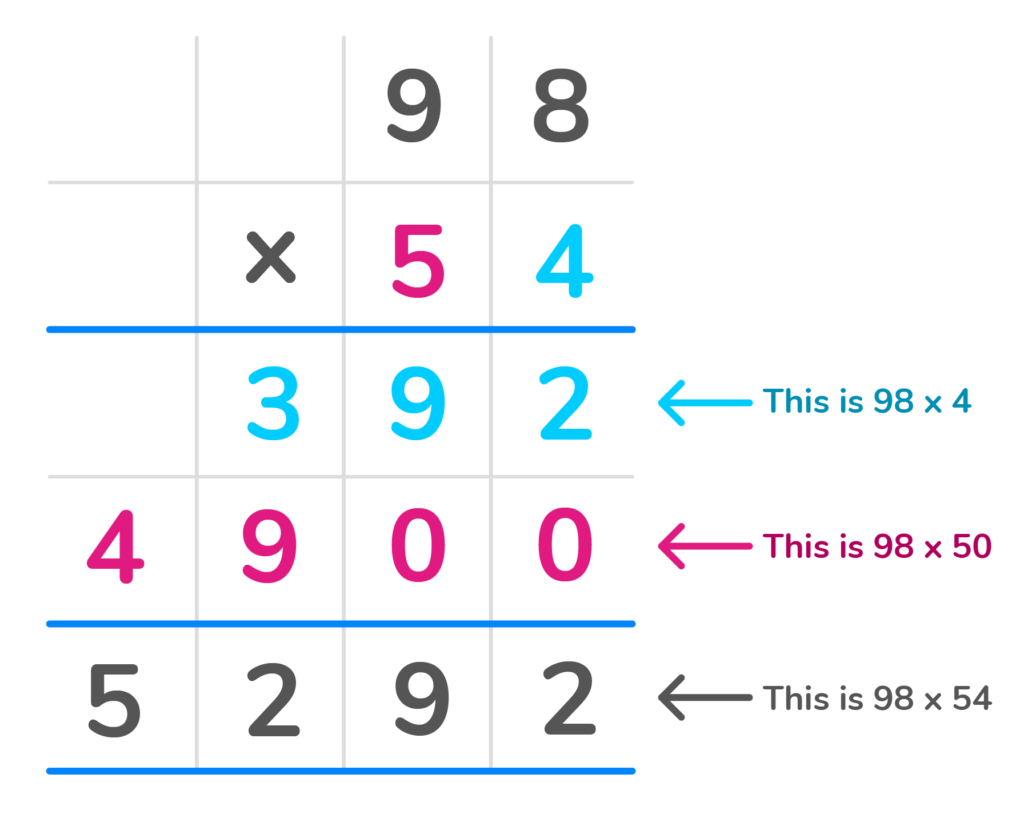
- Write the second number 54 in expanded form: 50 + 4.
- Multiply 98 times the first part 50. Multiply 98 x 5 and add a zero to the answer: 4,900.
- Next multiply 98 times the second part 4: 392.
- Finally, add those two partial products together: 4,900 + 392 = 5,292
FAQs About Long Multiplication
You do long multiplication by multiplying numbers in parts. You multiply each digit in the top number, by each digit in the bottom number. Finally, you add the partial products to get the final answer.
Long multiplication helps make multiplication with large numbers easy. The more you practice long multiplication, the easier these problems will be.
The long multiplication method is often called the column method. This is because the numbers you multiply are written above and below one another in columns.
You begin learning long multiplication in fourth grade and learn to multiply even larger numbers in fifth grade.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Amber Watkins
Hello, my name is Miss Amber. I am an Education Specialist with a degree in Early Childhood Education. I have over 12 years of experience teaching and tutoring elementary through college level math. I also create both video and written math content that has helped educate thousands of students online. Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!

