What Are Composite Numbers?
Learn the definition of composite numbers, how we use them in math and see a list of composite numbers 1 to 100

Author
Amber Watkins
Published:
March 2025
Key takeaways
- • Composite numbers include all natural numbers that have more than two factors.
- • Composite numbers are the opposite of prime numbers which only have two factors — one and itself.
- The first 10 composite numbers on a number line are 4, 6, 8, 9, 10, 12, 14, 15, 16 and 18.
In math, composite numbers make up a large part of the natural numbers that we know and use. What are composite numbers? Composite numbers include all natural numbers that have more than two factors.

- 6 is a composite number because it has more than two factors: 1, 2, 3 and 6.
- 2 is not a composite number because it only has two factors, 1 and itself.
Let’s learn more about composite numbers and how we can find them!
Table of contents
Get more math practice with DreamBox!
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Composite Number Definition
Composite numbers can be defined as any positive integers or natural numbers that have more than two factors. These factors usually include 1 and itself, along with at least one other value. In other words, composite numbers are the opposite of prime numbers, numbers that only have two factors.
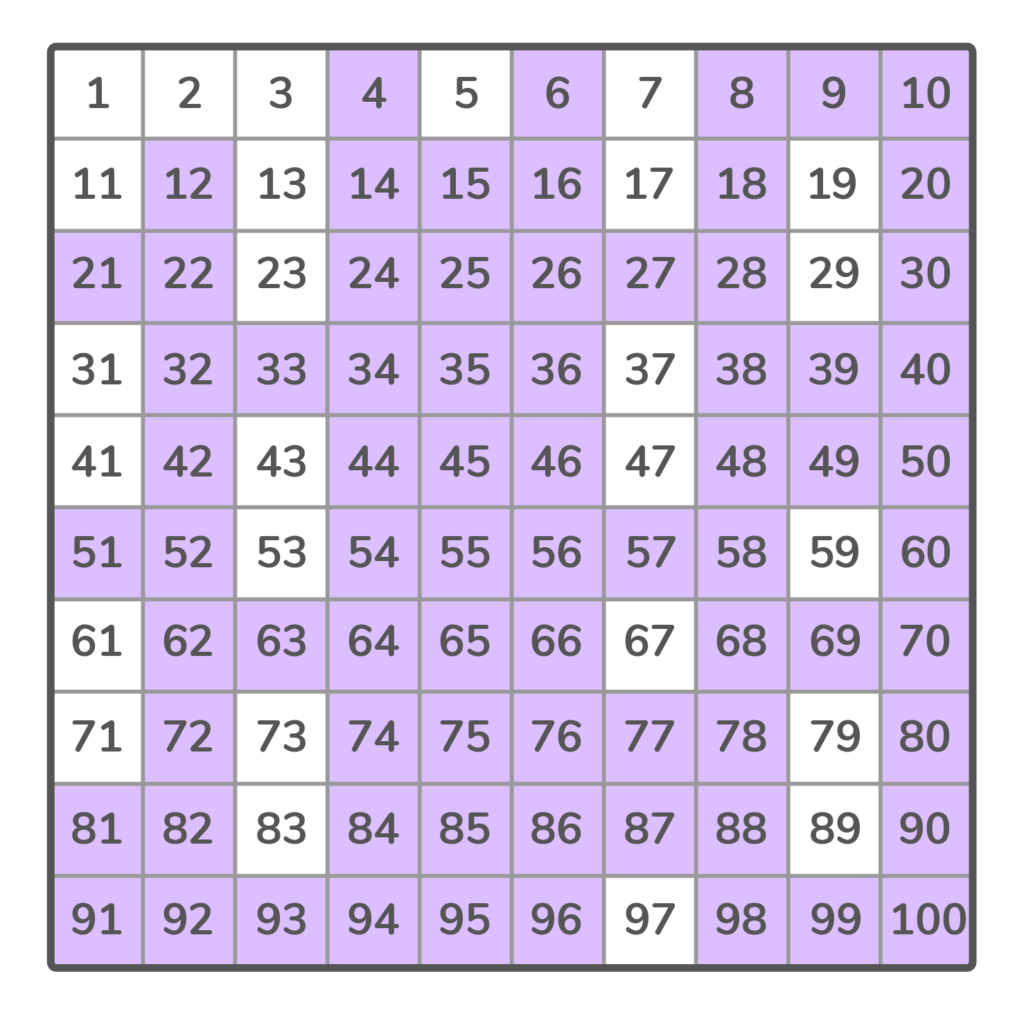
List of Composite Numbers up to 100
The list of composite numbers begins with the natural number 4. The first 10 composite numbers are {4, 6, 8, 9, 10, 12, 14, 15, 16, 18}. What makes these numbers composite?
That’s right, they all have more than two factors!
Factors are two numbers you multiply to get an answer.
For example: What are the factors of 6?
1 x 6 = 6
2 x 3 = 6.
So 1, 2, 3 & 6 are all factors of 6.
The Composite Numbers list from 1 to 100 is as follows: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Types of Composite Numbers
There are two types of Composite Numbers that you will see on a number line:
1. Odd Composite Numbers
2. Even Composite Numbers
Odd Composite Numbers
Odd composite numbers are any odd number that has more than two factors. This includes all positive odd numbers that are not prime numbers.
The list of odd composite numbers include: {9, 15, 21, 25, and 35}.
Can you use the Composite Numbers List 1 to 100 to name the next three odd numbers in the sequence?
Even Composite Numbers
Even composite numbers are any even numbers that have more than two factors. This includes all positive even numbers that are not prime numbers.
The list of even composite numbers includes: {4, 6, 8, 10, and 12}.
Can you use the Composite Numbers List 1 to 100 to name the next three numbers in the sequence?
What is the difference between Prime and Composite Numbers?
- The difference between prime numbers and composite numbers is the number of factors they have.
- Prime numbers only have two factors, while the composite number definition states composite numbers have more than two factors.
- A number can not be a prime number and a composite number.
Properties of Composite Numbers
- All composite numbers are divisible by 1 and itself
- All composite numbers are evenly divisible by its factors
- All composite numbers have more than two factors
- All composite numbers are divisible by prime numbers

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
How to Find the Composite Number
When we look at a number line, it is made up of prime and composite numbers. How can we identify which numbers are composite numbers?
Steps to find the Composite Number
- Find all the factors of a given number.
- If the number of factors is more than two, the number is a composite number.
- If the number of factors is only two, the number is a prime number.
Find the Composite Number by Prime Factorization
All composite numbers are divisible by prime numbers.
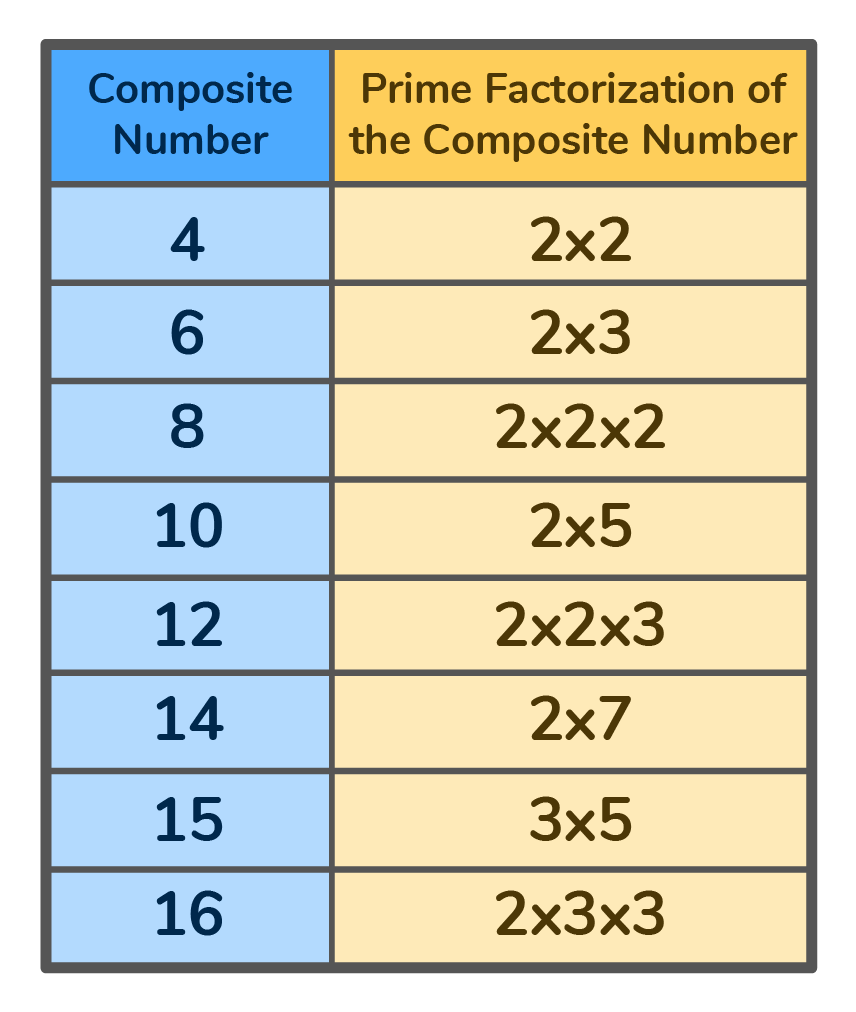
Prime factorization is the process of finding all the prime numbers that can be multiplied to equal the composite number. For example: The prime factorization for the composite number 20 is 2 x 2 x 5. The numbers 2 and 5 are both prime numbers, so we can use them to factor the number 20.
Steps to Factor a Composite Number by Prime Factorization
1. Choose a prime number to begin multiplying.
2. Continue by choosing other prime numbers to multiply until the multiplied total equals the composite number you are factoring.
The Prime Factorization of the first 10 Composite Numbers
Practice Problems
Click on the boxes below to see the answers!
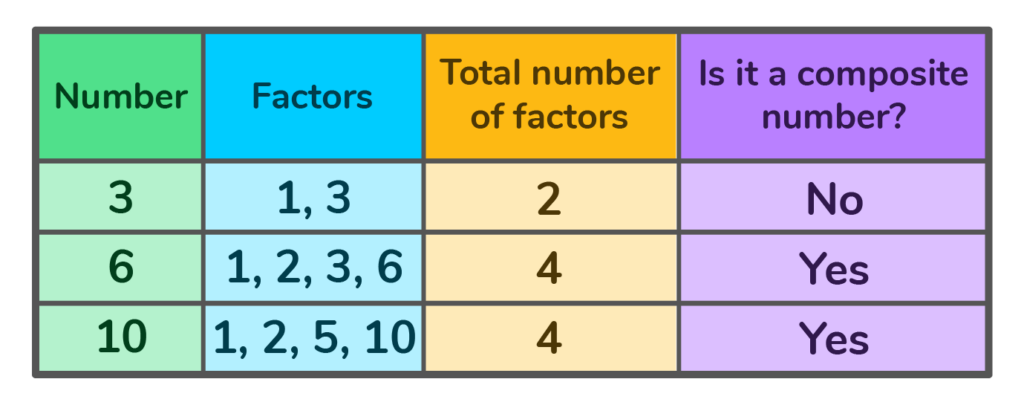
Yes, 10 is a composite number because it has more than two factors! { 1, 2, 5, and 10}.
No, it is not a composite number because it only has two factors {1 and 3}. Since 3 only has two factors, it is considered a prime number.
Yes, 6 is a composite number because it has more than two factors! { 1, 2, 3, and 6}.
FAQs About Composite Numbers
No, a number can not be both prime and composite. A prime number only has two factors. According to the composite number definition, a composite number has more than two factors. The number of factors clearly identifies a number as either prime or composite, not both.
The first 10 composite numbers are {4, 6, 8, 9, 10, 12, 14, 15, 16, 18}.
The smallest composite number is the natural number 4. The factors of 4 are 1, 2, and 4. It is the first natural number that has more than two factors.
No, all even numbers are not composite. The number 2 is an even number. However, it only has two factors: 1 and 2. Because the number 2 only has two factors it is a prime number, not a composite number.
No, the number 7 is not a composite number. The number 7 only has two factors: 1 and itself. Because the number 7 only has two factors it is a prime number, not a composite number.
No, zero is not a composite number. The number zero is neither prime nor composite.
Composite numbers are all natural numbers or positive integers that have more than two factors. A composite number can be odd or even, but never prime. To find a composite number, you must find all the factors to see if there are more than two.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


