What are irrational numbers?

You may have heard about irrational numbers, but what exactly are they? Let’s explore the definition of irrational numbers and famous irrational number examples.

Author
The Doodle Team

Published
August 2, 2023

What are irrational numbers?

You may have heard about irrational numbers, but what exactly are they? Let’s explore the definition of irrational numbers and famous irrational number examples.

Author
The Doodle Team

Published
August 2, 2023

What are irrational numbers?

You may have heard about irrational numbers, but what exactly are they? Let’s explore the definition of irrational numbers and famous irrational number examples.

Author
The Doodle Team

Published
August 2, 2023

Key takeaways

Irrational numbers are real numbers that cannot be expressed as a fraction.
An easy way to recognize if a number is irrational is if it never repeats or ends when written as a decimal.
Some famous examples of irrational numbers are Pi, Euler’s number, and the Golden Ratio.

Table of contents

The irrational number is said to have been discovered by the Greek philosopher Hippasus around the 5th century BC. At the time, his discovery was not met with the approval by others because most Pythagoreans believed only positive rational numbers could exist. The legend goes that he was made fun of for his discovery and thrown into the sea!

Thousands of years later, we now know numbers can be categorized as both rational and irrational. But what does this mean exactly? While it may seem complicated, once you understand what an irrational number is there is a very simple way to recognize them.

Irrational Numbers Definition

Put simply, an irrational number is any real number that cannot be written as a fraction. The fancier definition states that an irrational number cannot be expressed as a ratio of two integers–where p/q and q≠0. If a number cannot be written this way, it’s not a rational number. One clue that a number is irrational is if it never ends or never repeats when written as a decimal.

Here is a list of irrational number examples:

Decimals that do not repeat and continue indefinitely are the most common irrational numbers. They never end and can not be written as a fraction without rounding. For this reason, they are considered to be irrational, not rational.
Square roots that are not perfect squares are classified as irrational. You can enter the square root of the numbers 2, 13, or 18 into a calculator, but the answer you get will not be rational.

Irrational Numbers Examples

What are some ways you might see an irrational number? Some of the most famous irrational numbers are Pi, Euler’s Number, and the Golden Ratio.

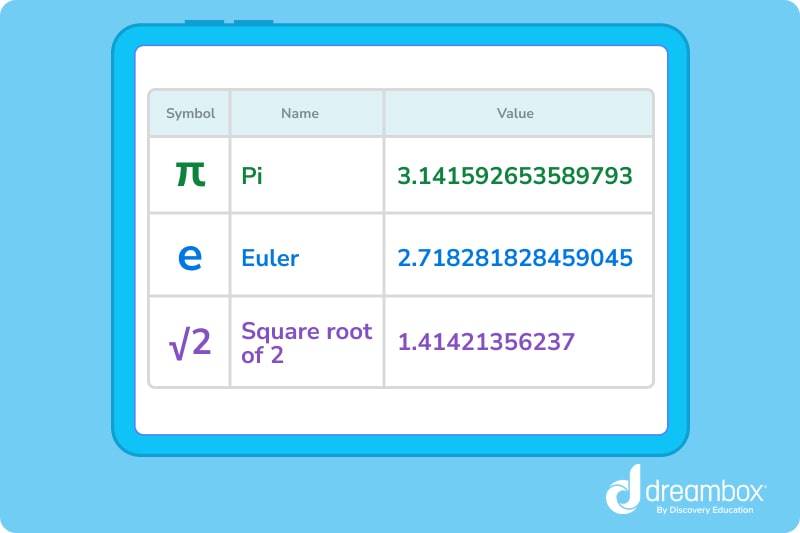
Pi, or π, is probably the most famous irrational number that’s known for it’s never ending decimal places. We estimate it to be around 22/7, but the exact number for Pi can never be a rational number.
Euler’s number is another famous irrational number that starts with 2.71828182845…..and so on. It is the often used in the complex math concept of logathrims.
The Golden Ratio φ is a famous ratio that approximately equals 1.618 (except it keeps going on and on). It is also known by the names Golden Mean, Divine Proportion, and Golden section.
Square roots and cube roots are often irrational. Unless a number is a perfect square or cube, it’s irrational. Have you tried to find the square root of 2? It can’t be written as a fraction, therefore, it’s an irrational number. However, 4 is a perfect square where √4 = 2, meaning it is a rational number.

Properties of irrational numbers

Since all irrational numbers are also real numbers, they obey the same set of properties as all real numbers. Here are some ways irrational numbers interact in the math world:

When adding an irrational number to a rational number, the sum is an irrational number.
When multiplying an irrational number by a rational number (not zero), the product is an irrational number.
When multiplying or adding two irrational numbers, the result could be rational.
When multiplying an irrational number by another irrational number, they may not have a least common multiple (LCM).

Difference between rational and irrational numbers

Irrational numbers and rational numbers are both valid numbers, even though they are displayed in different ways. In fact, they have more in common than you think.

Did you know that you can often multiply two irrational numbers (factors) to get a rational number (product)? Just because an irrational number may seem difficult to write or display, it can be very useful in math – just like a rational number.

The main difference between rational numbers vs irrational numbers is rational numbers can be written as fractions and irrational numbers cannot.

Ready for more practice?

Try the DoodleMath App for more practice with irrational numbers.

FAQs about irrational numbers

We know learning irrational numbers is complex so we’ve provided a few frequently asked questions many students or parents have when they start working with irrational numbers.

What’s the definition of irrational numbers?

Irrational numbers are numbers that can’t be written as a fraction.

How do you identify irrational numbers?

You can identify an irrational number by first turning it into a fraction. If it can’t be done, it’s likely irrational. Another clue is that many irrational numbers can be displayed as decimals that go on without an end or pattern. An example of this is Pi.

Are irrational numbers real numbers?

Irrational numbers are, in fact, real numbers. You can multiply them and add them to other numbers, just like rational numbers. While they aren’t always easy to work with, irrational numbers have an important place in math and our world.

What’s the difference between rational vs irrational numbers?

Rational and irrational numbers are both real numbers. Both types of numbers can be added, multiplied, and treated like any other number; you’ll just not be able to cleanly display irrational numbers as a simple ratio as you can with rational numbers.