All About Circles
Let’s learn about one of the most important – and perfect! – shapes in the world.

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- Circles are round shapes without any points, straight lines or angles – They don’t have to be perfectly round, though.
- There’s a lot to a circle – While circles may seem simple, there are a lot of different parts to a circle, including its diameter, its radius, and more.
- Understanding basic principles about circles will help in more advanced math classes – As students advance into middle and high school, finding the area of a circle will play a key part in subjects like geometry, trigonometry, and more.
Shapes are all around us — from square trucks to the round moon at night, the whole world is filled with shapes. It’s important to understand the principles behind a circle now. You’ll work with circles in class later on, and they are a part of your everyday life.
Let’s learn all about circles!
What defines a circle?
It might seem pretty simple to identify a circle, but there are a few key features a shape must have in order to be a circle. Essentially, circles around round shapes without any corners or edges.
Circles also have to be closed and two-dimensional. If a shape is a three-dimensional circle, it’s actually called a sphere. If a shape looks like a circle but isn’t complete, like a crescent moon, it might be called a “crescent” shape.
Some examples of objects that are circles
Take a look around, and you’ll find circles practically everywhere! The car you took to school this morning? Its tires are perfect circles. The plate you washed this morning is a circle, too!
Take a look up in the sky, and you’ll see that the Sun is a circle – just be sure not to stare right at it, since it’s the brightest circle around! Sometimes, the moon is a circle. Other times, it’s a crescent or a half-circle.
Let’s take a look at a few more examples:
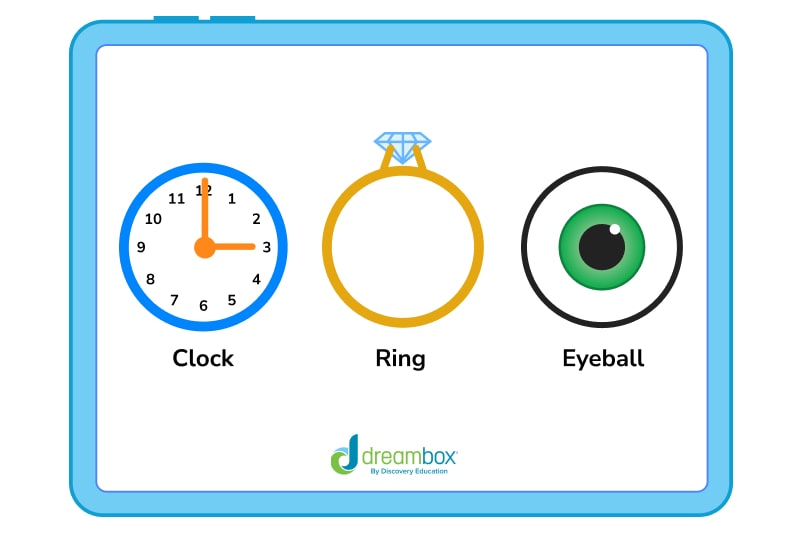
What about basketballs, globes, and crystal balls?
A circle is two-dimensional — you can’t pick a circle up and bounce it across the ground, or use a circle to gaze into the future. But, you can do these things with a sphere!
Basketballs, soccer balls, and other round objects that you can pick up and hold in your hands are spheres. Technically, so is the Sun we mentioned earlier, but from our perspective here on planet Earth, it’s still a circle — like a great, big, shiny penny in the sky.
Table of contents
Access more math practice with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Parts of a circle
There’s a lot more to a circle than just its shape. Let’s take a look at all the different parts of a circle.
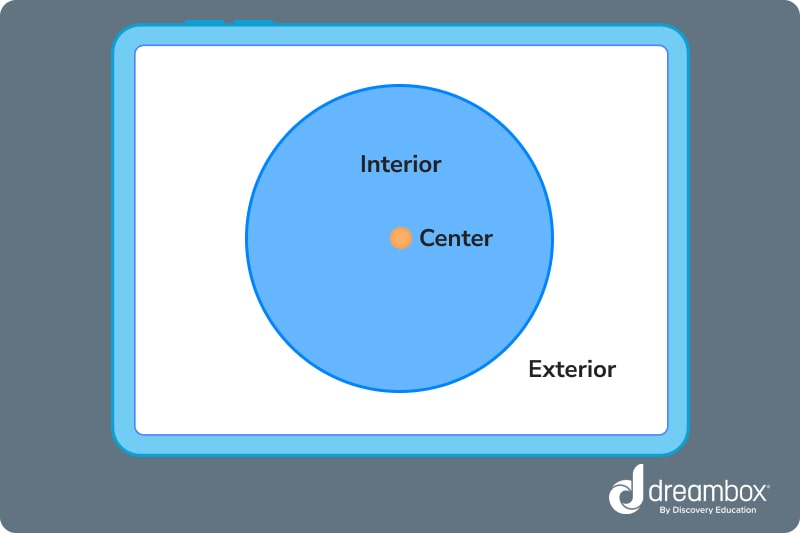
- The center of the circle. The center of a circle is the absolute center, and it’s important to know where that is if you want to measure different parts of a circle.
- The exterior of the circle. The exterior of the circle is everything that lies beyond the edge of the circle.
- The interior of the circle. The space between the edge of the circle and the center is the interior of the circle. Invisible lines run through the interior.
Let’s take a closer look at some of those invisible lines that run through the interior of a circle and learn how you can use them to find important measurements, like the circle’s area!
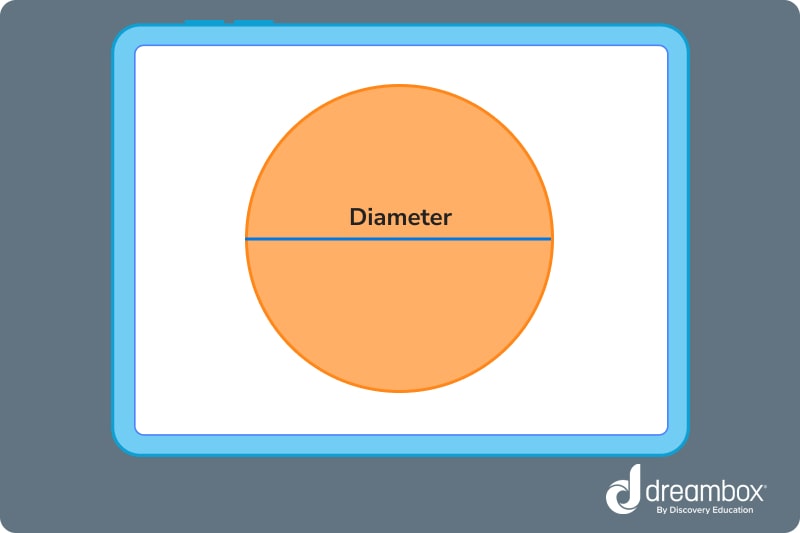
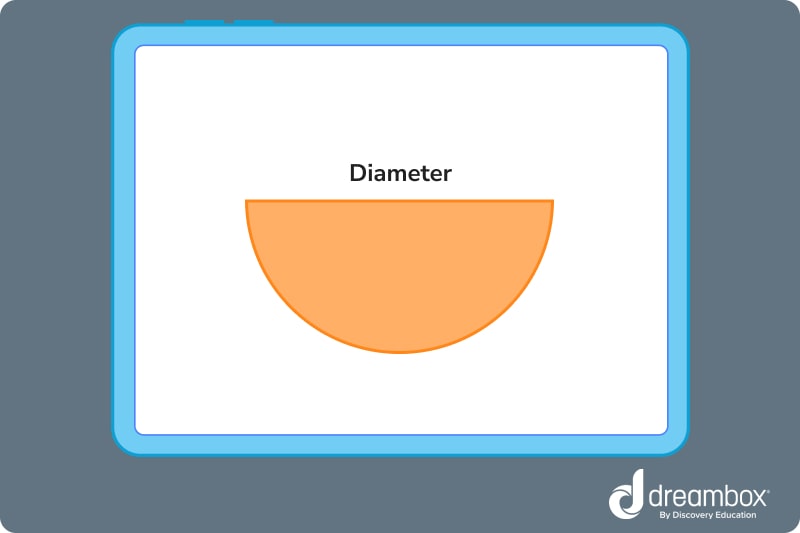
Diameter
The diameter of a circle measures from one side of the circle, through the center, and to the other side. This can be measured in different ways — from millimeters to inches or miles, depending on how big your circle is.
Radius
The radius of a circle is how much space is between the center to the outer edge. You can easily get the radius of the circle by dividing the diameter in half.
Circumference
Have you ever run around the outside of a track? Then you’ve run its circumference! A circle’s circumference is the distance around the circle. It’s the same as the perimeter of shapes with angles and straight lines.

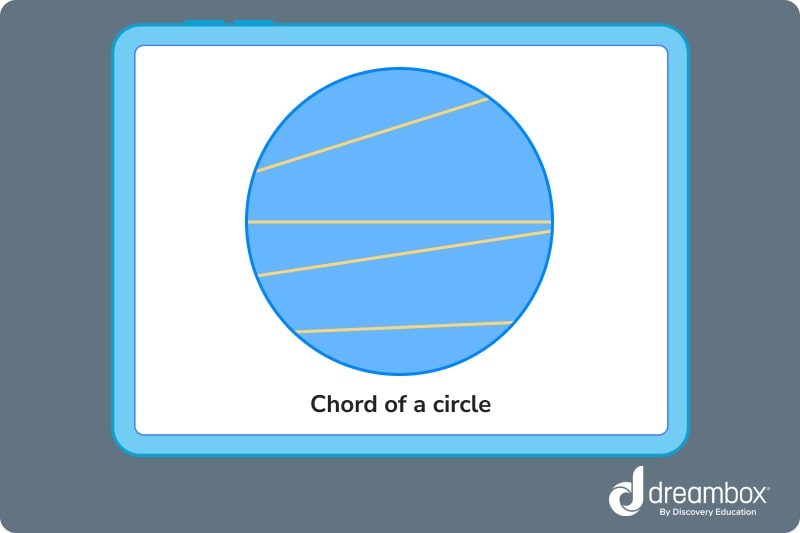
Chord of a circle
Chords in a circle are any line segments that go from one side of a circle to the other. As long as both endpoints of the line lay on the outer edge of the circle, then it’s a chord. Yes, the diameter of a circle is also a chord!
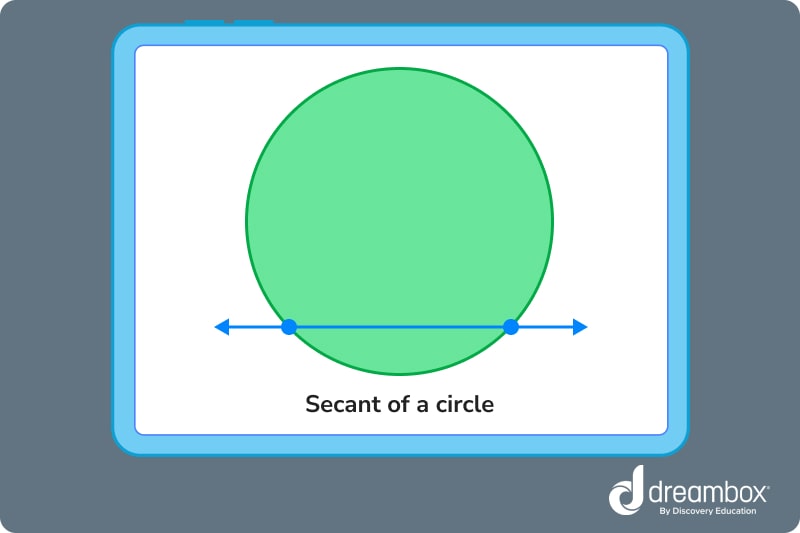
Secant of a circle
A secant is a straight line that intersects a circle in two places and continues on outside of the circle. Imagine that you lay your pencil down on top of a circular cookie. Your pencil is now a secant!
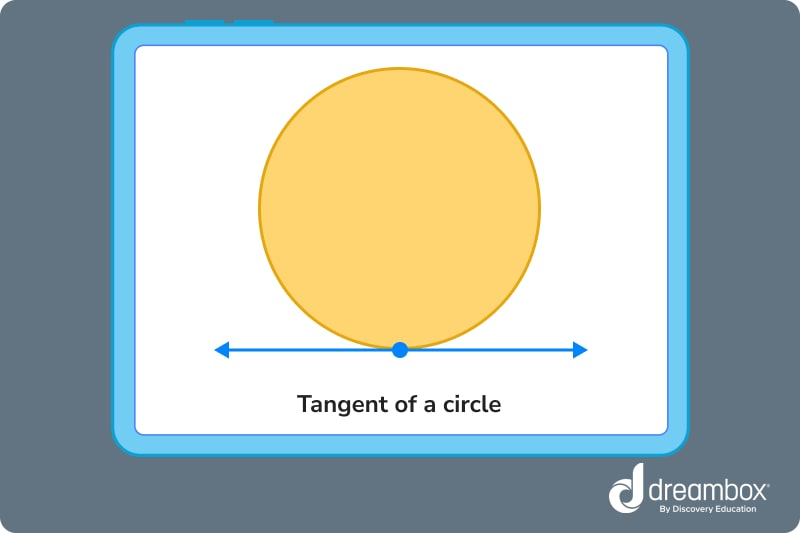
Tangent of a circle
A tangent is a line that’s outside of a circle, but that rests on the edge of the circle. For example, when a basketball is sitting on a shelf or a paved court, the surface it’s resting on is the tangent.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Splitting up a circle
Circles can be split up, too. For example, pizza slices are parts of a circular pizza. However, understanding how to split up a circle may help you cut more equal slices to make sure everyone gets the same amount! That’s one reason why math is so important: it helps you better understand how to make things truly equal.
Without math, it’s hard to divide up a circle equally.
Semicircle
Measure the diameter of a circle, cut along the diameter, and you make a semicircle. Put another way, if you cut a circle in half, you produce a semicircle.
Quarter circle

Finding a circle’s area
A circle’s area is how much space it takes up. Above, we talked about how the diameter can be measured in millimeters or miles. This, and the number for pi, is all you need to know to find the circle’s area.
Use this formula to find a circle’s area:
A = π x r2
In this formula, A = area, which is what we’re trying to find. Pi, or Π, is a ratio we use for the circumference of circles. Then, we use the radius multiplied by itself to solve for the area.
Pi is equal to 3.14.
Why does it say r2? The little 2 next to the r represent the practice of squaring. Basically, squaring is a quick way to say that whatever r is, you multiply it by itself.
Here’s an example:
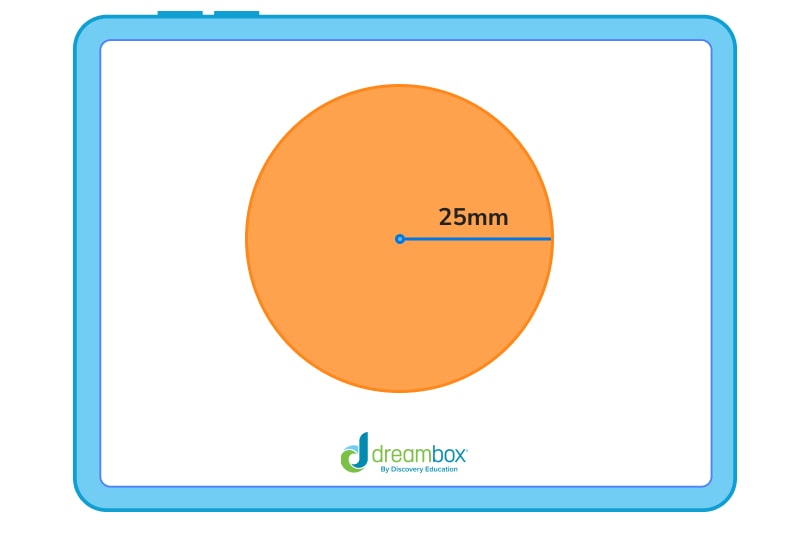
The circle below has a radius of 25mm.
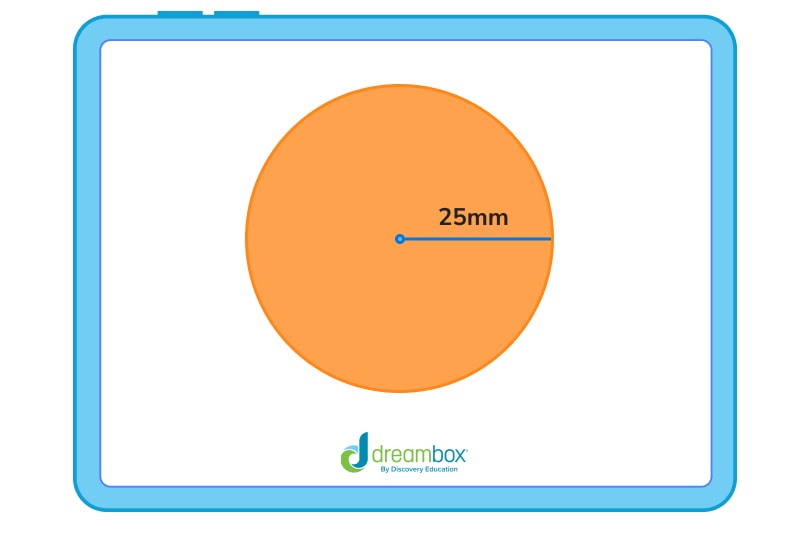
To find the area, we would plug the right numbers into the formula, like this:
A = 3.14 x 252
25 mm x 25 mm = 625 mm
625 mm x 3.14 = 1,963 mm
1,963 mm = 3.14 x 252
Understanding what a circle is and how to find its area is foundational to understanding more advanced mathematics, like geometry and trigonometry. Keep practicing to build your confidence and become a circle master!
Circle practice problems
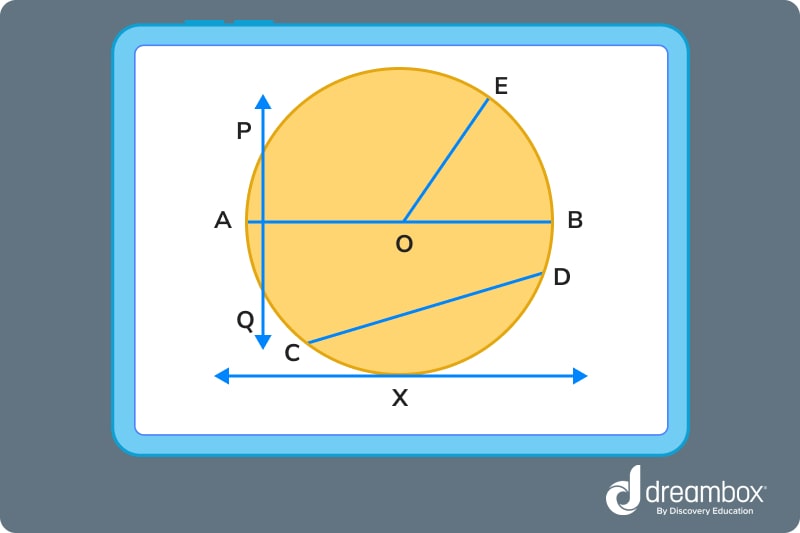
Now that you know the parts of a circle and how to measure them, take a look at the figure and answer the problems below!
- Which line segment represents the diameter?
- And, which line segments are the radius?
- What two lines are the secant and tangent?
- What’s the area of a circle with a radius of 24in?
- If a circle has a radius of 18mm, what’s the area?
Parent Guide
-
1. The answer is line O. How did we get here?
- The diameter of a circle is the width of it through the exact center. Students can find this by identifying the line that passes through the center of the circle and touches both outer edges. In our illustration, that’s line O.
-
2. The answer is line E. How did we get here?
- The radius is the width from the center of a circle to the outer edge. In our illustration, that’s line E.
-
3. The answer is line X. How did we get here?
- The secant line is a line that touches a circle at the same, opposite two points. In our illustration, that’s line C-D. The Tangent only touches the outer edge at one point, and in our illustration, that’s line X.
-
4. The answer is 1,809 inches. How did we get here?
- 1. To find the area of a circle with a radius of 24in, use the formula A = π x r2
2. Multiple 24 by 24 (576)
3. Then, multiply that number by π (3.14)
4. The result will be to get 1,809 inches. -
5. The answer is 1,017 mm. How did we get here?
- 1. To find the area of a circle with a radius of 18mm, use the formula A = π x r2
2. Multiple 18 by 18 (324)
3. Then, multiply that number by π (3.14)
4. The result will be to get 1,017 mm
FAQs about circles
The diameter of a circle is a straight line segment that passes through the center of the circle and connects two points on the edge (called the circumference) of the circle. It is the longest distance you can measure within a circle.
The size of a circle is typically measured using its radius or diameter. The radius is the distance from the center of the circle to any point on the edge. The diameter is the distance across the circle passing through the center.
We can use these measurements to calculate other important quantities like the circumference (distance around the circle) and the area (the space inside the circle).
Pi (π) is a special mathematical constant that is related to circles. It represents the ratio of the circumference of any circle to its diameter. No matter the size of the circle, this ratio remains the same.
Pi is approximately equal to 3.14159, but it goes on infinitely without repeating any pattern. Pi is important in many mathematical calculations involving circles, such as finding the circumference or the area.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

