All About Hexagons
Discover the ins and outs of this versatile six-sided shape.

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- • Perpendicular lines are two straight lines that meet or intersect at 90°.
- • The opposite of perpendicular lines are parallel lines. Unlike perpendicular lines, parallel lines never intersect.
- • The equation of a line that is perpendicular is y = mx + c.
- A hexagon has six sides – They are two-dimensional closed figures, and they can be oddly shaped, so long as their sides add up to six.
- There are different kinds of hexagons – Regular hexagons have equal sides and equal angles, while irregular hexagons can bend the rules a little.
- The hexagon shape is popular in nature – Beehives, insect eyes and more feature hexagons because of their ability to fit together seamlessly.
Have you ever stared at a beehive and thought, “Wow, those shapes are really cool!”? What you’ve actually been looking at are natural hexagons – six-sided polygons that fit together perfectly!
So what is a hexagon, and how can we measure its perimeter, area, and more? Let’s take a closer look at this unique shape
What is a hexagon?
A hexagon is a six-sided polygon with six interior angles. There are two different types of hexagons – regular and irregular hexagons.
To be considered “regular,” a hexagon must have six equal sides and six angles that each measure 120°.
So where does the word “hexagon” come from? Well, the prefix “hexa” means six, and “gonia” means angles. Put that together, and you get “six angles,” a requirement for a shape to be called a hexagon!
Hexagons in the real world
Hexagons are some of the most naturally occurring shapes in the world! That’s because six sides tend to fit together perfectly to make a strong, dynamic shape or design. You’ll see hexagons when you study beehives, insect eyes, and the center of snowflakes.
Ever kicked a soccer ball around? The black and white designs that make up the outside of the ball are hexagons! They are also a popular choice for tile floors, given they fit so neatly together.

Table of contents
Get more math practice with DreamBox!
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Must-have properties of a hexagon
Fortunately, hexagons don’t have as many rules to follow as, say, a square, a rectangle, or a triangle.
Basically, a hexagon has:
- 6 sides
- 6 angles
- 6 vertices
See the major pattern here? Six, six, six! However, there are different types of hexagons, and each of them have their own set of rules. Let’s take a look at these different types together.
Types of hexagons
Regular hexagons
Regular hexagons follow more rules than other types of hexagons. In order to be considered a regular hexagon, the shape must have:
- 6 equal sides
- 6 vertices
- 6 interior angles that each measure 120°
If you’re calculating the perimeter of a regular hexagon, you simply need to multiply the length of one side by 6 to get the perimeter of the entire shape.
Some other fun facts about a regular hexagon:
- All exterior angles measure 60°
- The shape can be divided into six equilateral triangles
- The opposite sides of a regular hexagon are parallel to each other
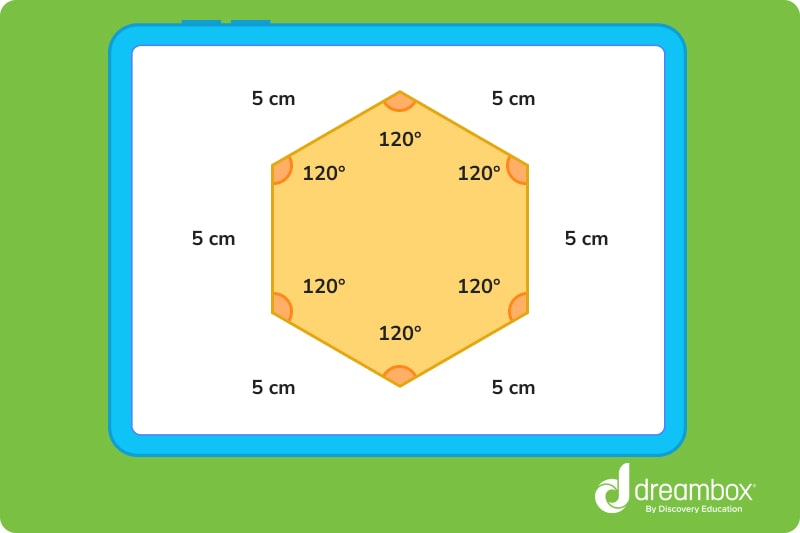
Convex hexagons
Every regular hexagon will also be a convex hexagon. When something is convex, it means that it only has interior angles. In a regular hexagon, all angles must be interior, so a regular hexagon is also a convex hexagon.
Irregular hexagons
When we think about the word irregular, we think about “strange” or a little whacky, right? Think about irregular hexagons in the same way. They still have to have six sides, and they must be a closed shape, but outside of that, they get to break the rules.
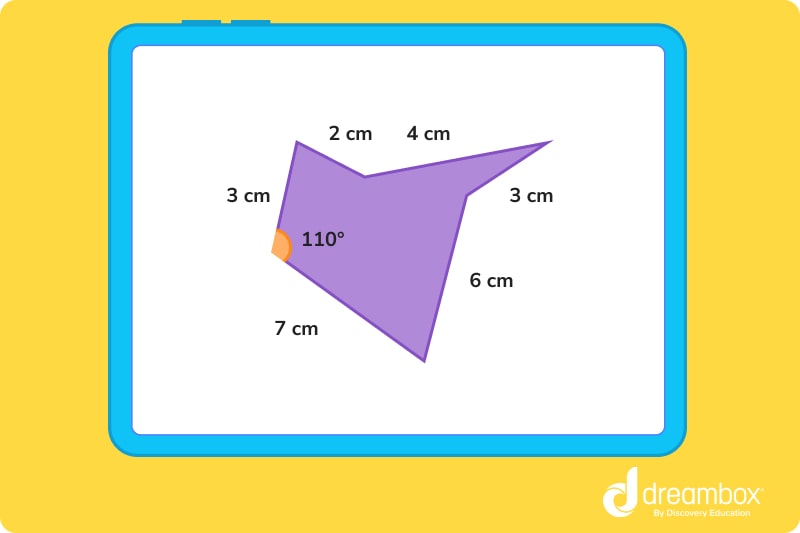
Concave hexagons
The word “concave” literally has the word “cave” in it, right? In a concave hexagon, at least one of the angles will be an exterior angle, which may make the shape look like it has a mouth!
Concave hexagons still have to have – you guessed it – six sides! But two of those sides will likely point inward rather than creating a smooth, round perimeter.
What can we measure about a hexagon?
Shapes like circles and squares have specific formulas for measuring area and perimeter. There is a formula to measure the area of a hexagon, but you likely will not need it until much later in your academic career.
We are going to focus on the measurement you’ll likely need to calculate once you start working with hexagons: perimeter.
The perimeter of a hexagon
You probably know that the perimeter of any shape is the measure of its exterior sides. To calculate the perimeter of a hexagon, simply add up each of the shape’s sides.
For a regular hexagon, you can do this pretty easily. Simply use the measurement of one side, then multiply that number by 6.
For an irregular hexagon, you will want to add up each of the sides on your own.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Let’s practice together!
1. Identify the regular hexagon.
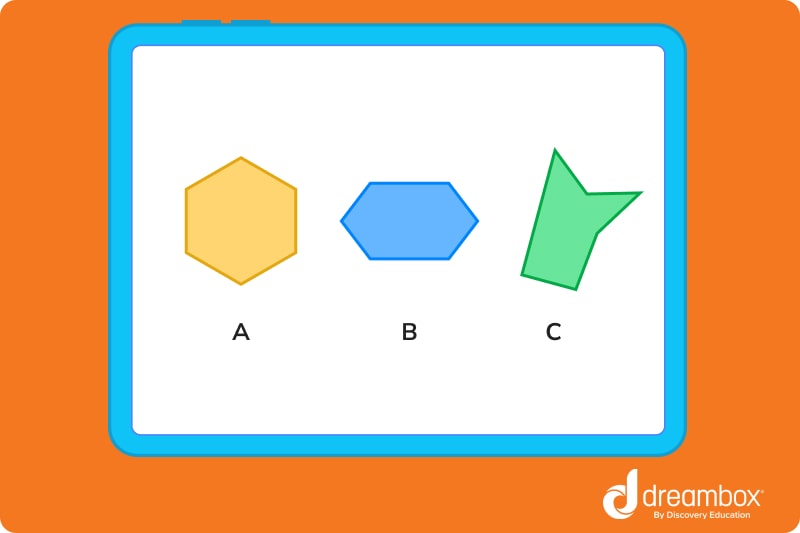
The correct answer is A. A is the only hexagon that has 6 equal sides and 6 equal angles. Both B and C are irregular hexagons.
2. True or false: Figure C in question #1 is a convex hexagon.
The answer is FALSE. Figure C is actually a concave hexagon, while Figures A and B are convex hexagons. See how Figure C has a piece that looks like a cave or a mouth? That’s how you can tell!
3. What is the perimeter of a regular hexagon with one side that measures 7 inches?
Since we’re calculating the perimeter of a regular hexagon, we know that we can multiply one side by 6 to get the perimeter.
So, 7 × 6 = 42 inches.
Ready to give it a go?
-
It’s time to put your knowledge of hexagons to the ultimate test! Work through the following problems on your own. Feel free to look back at the practice problems above if you get stuck, or use the guide to refresh your memory.
And remember, don’t get discouraged if you run into a roadblock! Practice is the best way to learn something new.
Hexagon practice problems
Click to reveal the answer.
The answer is 60 inches.
The answer is 30 inches.
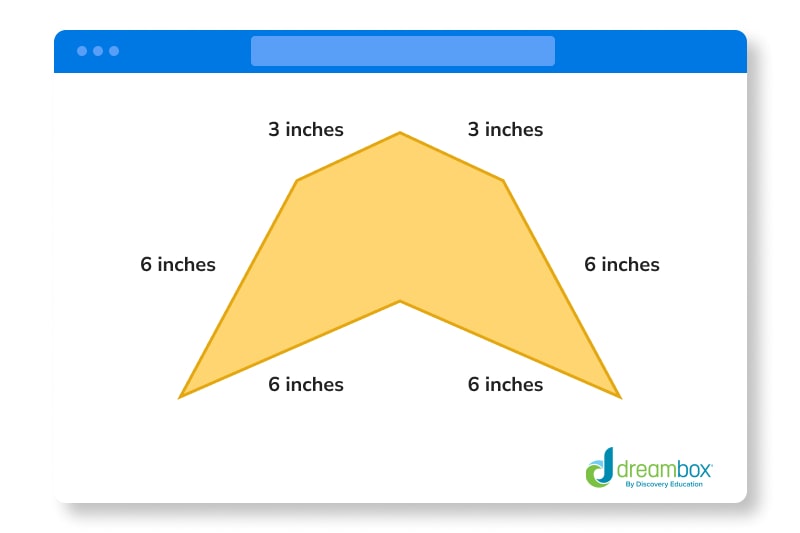
The answer is false.
The answer is 30 inches.
The answer is true.
Parent Guide
-
1. The answer is 60 inches. How did we get here?
- 1. Since this is a regular hexagon, we can assume that all sides are equal.
2. Multiply 10 by 6, or add 10 together 6 times to get 60 inches. -
2. The answer is 30 inches. How did we get here?
- 1. For an irregular hexagon, you have to add all the sides together.
2. We can make this a bit quicker using multiplication. 4 sides equal 6 inches, so 6 × 4 = 24. 2 sides equal 3 inches, and 3 × 2 = 6.
3. Then, we add 24 inches and 6 inches together to get 30 inches. -
3. The answer is false. How did we get here?
- 1. It’s true that all regular hexagons are convex, but not ALL convex hexagons are regular.
2. You can have irregular convex hexagons.
3. That means the answer must be false. -
4. The answer is 30 inches. How did we get here?
- 1. Since this is a regular hexagon, we can assume that all sides are equal.
2. Multiply 5 by 6, or add 5 together 6 times to get 30 inches. -
5. The answer is true. How did we get here?
- Since concave hexagons include at least one exterior angle, they cannot be regular hexagons, which must have 6 interior angles that measure 120°.
FAQs about hexagons
No, not all six-sided shapes are called hexagons. A hexagon is a specific type of six-sided shape with straight sides. It has six angles and six sides that are all equal in length. Each side of a hexagon connects to two other sides, and it has a total of six corners, which are called vertices.
No, not all hexagons have equal sides. A hexagon is a polygon with six sides, but its sides can have different lengths. A hexagon with equal sides is called a regular hexagon. In a regular hexagon, all six sides are the same length, and all six angles are equal.
The hexagon is often considered a strong shape because it distributes forces or weight evenly across its sides. This means that when you push or pull on a hexagon, the pressure or force is spread out more evenly compared to other shapes.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

