All About Squares

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- Squares have four equal sides and four equal angles – These regular polygons are two-dimensional enclosed figures.
- There are three parts to a square – While squares are simple, there are three parts to notice including the length, width, and diagonals.
- Understanding basic principles about squares will help later on – As students advance into middle and high school, finding the area and perimeter of a square will play a key part in subjects like geometry, trigonometry, and more.
Squares are everywhere — and they’re pretty easy to spot once you can recognize the shape! It’s important to understand the must-have principles that a shape needs to be a square, though. Let’s learn all about squares!
What is a square?
A square is a regular polygon with four equal sides and equal angles that each measure 90°. For a quick refresher, a regular polygon is a two-dimensional enclosed figure made by joining three or more straight lines. Now, let’s identify some real world examples of squares!
Squares in the real world
You come across squares every day, and you might not even realize it! Everyday items like picture frames, sticky notes, and pizza boxes are just a few examples out of hundreds. Take a look at the images below for some visual examples, then take a look around your room — can you identify three square shapes objects?

Table of contents
Strengthen your math skills with DreamBox
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Must-have properties of a square
There are certain properties that a shape must have in order to be a square. Keep an eye out for the following must-haves to determine if something is a square:
- It has 4 sides and 4 vertices
- Its sides are equal in length
- All interior angles are equal and right angles, meaning each angle measures 90°
- The sum of all the interior angles is 360°
- Its two diagonals bisect each other at right angles
Parts of a square
The best way to learn anything in math is to break it down into its parts — it’s so much easier to understand! Let’s take a look at the three different parts of a square.
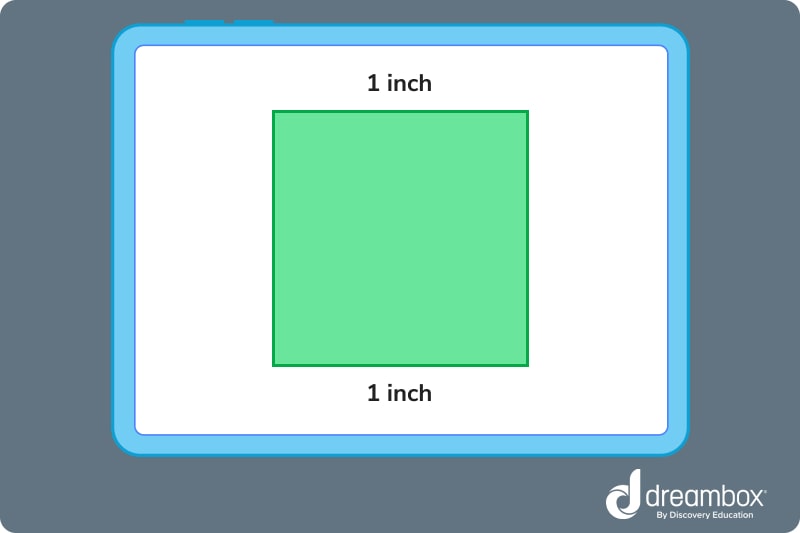
Length
The length of a square is best described as the top and bottom lines of the square, as shown below.
Width
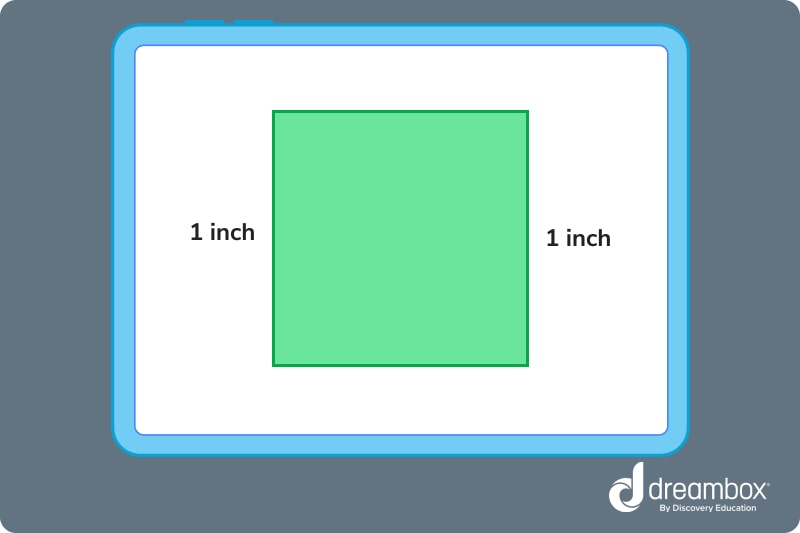
The width of a square is simply the left and right-hand sides of a square, as shown below.
Diagonals
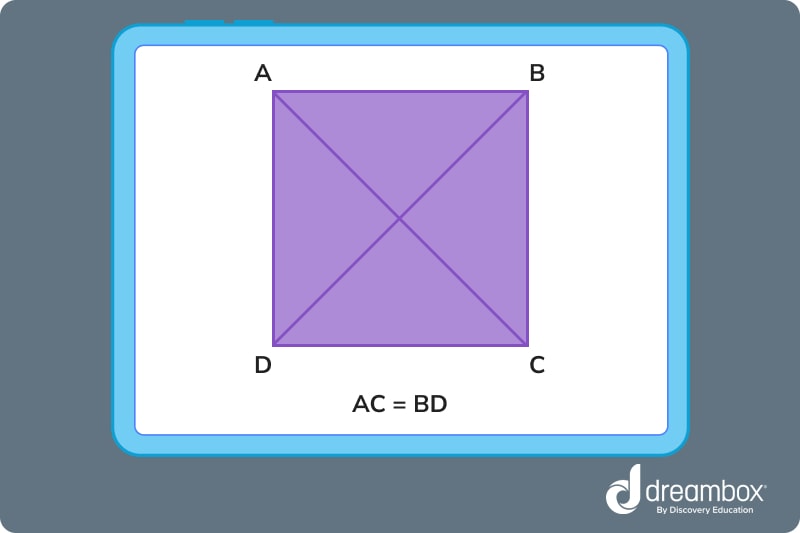
The diagonal of a square is a line that connects one corner to the opposite corner through the center, as shown below. A square has two diagonals that are equal in length, and they bisect each other at right angles.
What can we measure with the parts of a square?
Once you’ve identified that something is a square, then you can measure it! We can measure the area and the perimeter of a square with two easy formulas.
Perimeter
The perimeter of a square is the length of the outer boundary of the shape. For a square of side length “S” units, the perimeter is presented as the following formula:
Perimeter = side + side + side + side = 4 × S
The perimeter of a square is expressed in linear units like centimeters (cm), inches (in), meters (m), etc.
Area
The area of a square is the amount of space covered by the shape if we were to keep it on a flat table. For a square of side length “S” units, the area is presented as the following formula:
Area = side × side = S2
The area of a square is expressed in square units like cm2, m2, etc.

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Let’s practice together
1. Identify the square in the following group of shapes:
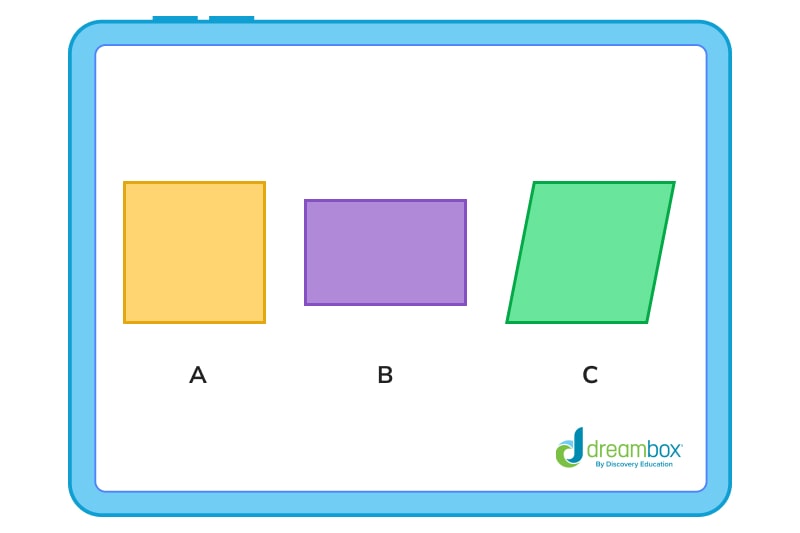
The correct answer is A. Figure A has equal sides and interior angles that all measure 90°. Figure B is a rectangle, with its length different from its width, and C is a parallelogram, with interior angles that do not equal 90°.
2. Find the perimeter of a square that has four sides measuring 5 inches each.
Remember, each side of a square is equal to the other side. That means we have 4 sides that equal 5 inches. So the perimeter is 5 + 5 + 5 + 5 or 4 × 5, which equal 20 inches.
3. Find the area of a square that has four sides measuring 11 cm each.
The area of a square is the measure of its length × its width. So, if we multiply 11 × 11, we get 121 cm2.
Ready to give it a go?
-
Now that you know how to identify a square, the parts of a square, and how to measure them, we’re ready to do a few practice problems! Work through the following problems on your own. Feel free to look back at the practice problems above if you get stuck, or if you need a quick reminder on what a square is or how to measure its parts.
And remember, don’t get discouraged if you run into a roadblock! Practice is the best way to learn something new.
Practice Problems
Click to reveal the answer.
The area is 64 sq. ft.
The perimeter is 24 inches.
The perimeter is 48 inches.
The area is 625 sq. cm.
The measure of its side is 14 cm.
Parent Guide
-
1. The area is 64 sq. ft. How did we get here?
- 1. Read the problem: The side of a square is 8 feet. Find the area.
2. We know that to find the area of the square, we use this equation: side x side = S2
3. We also know that S = side
4. For the given square, S = 8 feet
5. Then, we can plug 8 into the equation. So, area = S2 = 8 x 8 = 64 sq. ft. -
2. The perimeter is 24 inches. How did we get here?
- 1. Read the problem: The side of a square pizza box is 6 inches. Find the perimeter.
2. We know that to find the perimeter of the square, we use this equation: side + side + side + side = 4 x S
3. We also know that S = side
4. For the given square pizza box, S = 6 inches
5. Then, we can plug 6 into the equation. So, perimeter = 6 + 6 + 6 + 6 or 4 x 6 = 24 inches. -
3. The area is 625 sq. cm. How did we get here?
- 1. Read the problem: What is the perimeter of a square that has a side of 12 inches?
2. We know that to find the perimeter of the square, we use this equation: side + side + side + side = 4 x S
3. We also know that S = side
4. For the given square, S = 12 inches
5. Then, we can plug 12 into the equation. So, perimeter = 12 + 12 + 12 + 12 or 4 x 12 = 48 inches. -
4. The area is 625 sq. cm. How did we get here?
- 1. Read the problem: What is the area of a square with a side length of 25 cm?
2. We know that to find the area of the square, we use this equation: side x side = S2
3. We also know that S = side
4. For the given square, S = 25 cm
5. Then, we can plug 25 into the equation. So, area = S2 = 25 x 25 = 625 sq. cm. -
5. The measure of its side is 14 cm. How did we get here?
- 1. Read the problem: If the perimeter of a square is 56 cm, what is the measure of its side?
2. We know that the perimeter of a square is given by 4 x S
3. We also know that the perimeter of the square is 56 cm
4. So, 4 x S = 56
5. Now, we have to divide 56 by 4 to find the measure of the side.
6. 56 ÷ 4 = 14 cm
FAQs about square shapes
What makes a square a square is how equal its sides are. To be a square, a polygon must have four sides of equal length and four right angles. All squares are rectangles, but not all rectangles are squares.
Why? Because the length of a rectangle doesn’t have to equal its width. To be a square, all sides have to be equal.
To measure the area of a square, simply multiply its length and its width. For example, say you have a square with sides that equal 4 inches. You would multiply 4 by 4 to get 16 inches.
Squares are important because they play a major role in construction, decoration, and artistic expression. They are one of the few shapes that can fit together perfectly, making them the best choice for projects like tile floors or roof shingles.
Without squares, we also wouldn’t have fun board games like Monopoly or CandyLand, where you have to land on squares to move forward. And we can’t forget Four Square, one of the best games to play with friends!
In exciting fields like design, many people say that the square represents strength and stability. This is because of its equal sides and equal angles. Some psychologists say that many people associate the square with truth and consistency, since it is uniform all the way around.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

