All About Pentagons
Learn all about the 5-sided shape that’s so fun, they named a government building after it.

Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- Pentagons are 5-sided polygons – “Penta” means “five,” so it’s easy to remember how many sides you’re dealing with when you see the word “pentagon.”
- Finding the perimeter of a regular pentagon is easy – Since regular pentagons have equal sides, just multiply the length of the sides by 5 to find the answer.
- Figuring out the area of irregular pentagons is a bit tricky – While there’s a straightforward formula for the area of a regular pentagon (read on to find out more!), irregular pentagons require knowledge of other area formulas, like how to calculate the area of a triangle!
Today, we’ll be discussing our five-sided friend, the pentagon! From a common stop sign to the tiles on your bathroom floor, pentagons are a common shape you’ll run into in your everyday life. It might be nice, then, to understand how they work and the kinds of formulas we can use to calculate their perimeter and their area.
Ready to dive in? Let’s get going.
What is a pentagon?
A pentagon is a five-sided polygon with five interior angles that add up to 540°. It’s another one of our classic 2-D shapes, meaning it exists on a flat plane just like your average triangle, square or circle.
What does a pentagon look like?
If you’ve ever played baseball or softball, a pentagon is the same shape as home plate. There are five sides in total with five angles at each of the shape’s vertices (the points where lines join to form angles).
Parts of a pentagon
There are a few key parts you’ll need to know in order to identify the perimeter or area of a pentagon. These include:
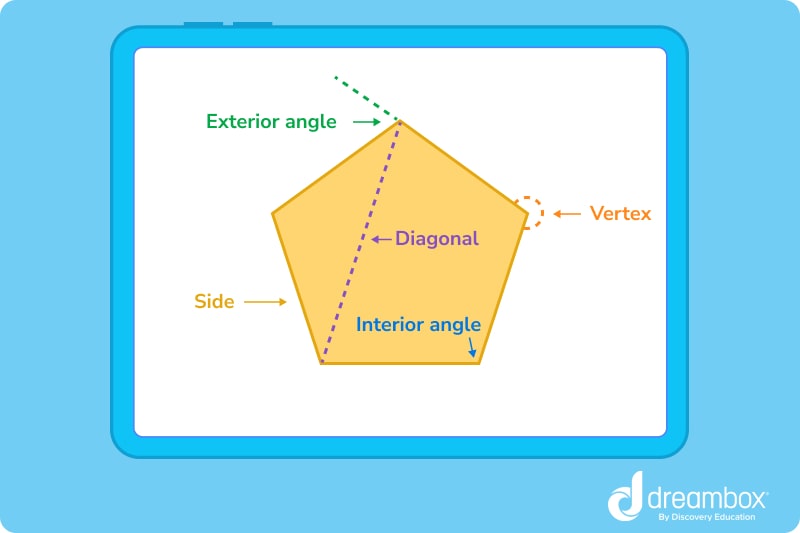
- Side – These are the five line segments that form the shape of a pentagon.
- Vertex – The vertices are the points at which each of the five line segments meet. Each pentagon has five vertices. Treat a vertex the same way you would treat a corner.
- Diagonal – A diagonal is a line that connects vertices that are non-adjacent (not right next to each other). When these two corners are connected, the line segment that connects them is known as a diagonal. There are five diagonals as well.
- Interior angle – An interior angle includes any of the angles that form at the point where the sides meet (the vertex). There are five interior angles to match with the five vertices and five sides, and the sum of these interior angles is 540°.
- Exterior angle – There are also five exterior angles, each of which is formed outside of the pentagon’s shape. For every interior angle, there is a corresponding exterior angle.
- Apothem – A line drawn from the center of any polygon to the midpoint of one of the sides.
Real-life examples of pentagons
There are a few key parts you’ll need to know in order to identify the perimeter or area of a pentagon. These include:

Did you know? The headquarters for the U.S Department of Defense is actually named The Pentagon, and it’s shaped just like one too!
Table of contents
Get more math practice with DreamBox!
Turn math into playtime with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Types of pentagons
There are a few different categories of pentagons we’ll encounter including regular pentagons, irregular pentagons, convex pentagons, and concave pentagons. You can identify the kind of pentagon you’re dealing with by identifying the types of angles the pentagon has, what the sums of these angles are, and how the pentagon itself is shaped. Follow along as we examine the four different categories of our five-sided friends.
Regular pentagons
Regular pentagons have five equal sides and five equal interior angles. If each of the five sides have an equal length, and each of the five angles have an equal measurement, the pentagon is considered regular. Just remember: regular means equal.
Irregular pentagons
Irregular pentagons are defined as pentagons with unequal values for both side length and angle measurements. Because of this, irregular pentagons aren’t symmetrical and will look more elongated or flattened.
Convex pentagons
Convex pentagons are unique because all of their vertices point outward. This means that none of the sides of a convex pentagon point inward. Each of them point outward to create an outward facing vertex.
Concave pentagons
Concave pentagons are the opposite of convex, because they include at least one vertex that points inward. Think of the meeting of each side as the formation of an arrow. If the point of the arrow (the vertex) is facing inward, the shape is concave. If it faces outward, the shape is convex!
Perimeter of a pentagon
Finding the perimeter of a pentagon is the same process as finding the perimeter of any other kind of shape. All you need to do is find the sum of each of the five sides, and you’ll have calculated the perimeter of the pentagon. This process is the same regardless of whether the pentagon is regular, irregular, convex or concave.
However, finding the perimeter of a regular pentagon is a whole lot easier than finding the perimeter of an irregular pentagon: all you have to do is multiply the side length by 5!
Area of a pentagon
Finding the area of a pentagon is a bit more complicated than finding its perimeter, as you’ve probably already expected. The method you use to calculate the pentagon’s area depends on whether you’re dealing with a regular or irregular pentagon. Let’s walk through the steps of how you’d calculate the area of both.
Area of a regular pentagon
Finding the area of a regular pentagon is easy, so long as you have the apothem and the measure of one of the sides! Later, you may be asked to find the apothem of a pentagon. For now, though, let’s assume that you are given the apothem when you’re asked to find the area.
1. There’s an easy formula that will help you find the area of a regular pentagon:

2. So, first we need to find the perimeter. This should be easy! A regular pentagon has 5 equal sides, so we’ll just need to multiply the length of the sides by 5 to find our perimeter.
3. Then, we’ll take the apothem and the perimeter and plug in the values to find our area!
So let’s say we have a regular pentagon with a side length 5 cm and an apothem of 3.44 cm.
1. We will first find the perimeter of the regular pentagon: 5 x 5 = 25
2. Then, we will use our formula: 1/2 x Perimeter x Apothem sq units = 1/2 x 25 x 3.44 cm²
3. 25 x 3.44 cm² = 86 cm² x 1/2 = 43 cm²
Remember, this formula is for finding the area of a regular pentagon. The method for finding the area of an irregular pentagon is something you won’t see until much later in your math career!

The math program that drives results
Get started today!
DreamBox adapts to your child’s level and learning needs, ensuring they are appropriately challenged and get confidence-building wins.
Let's practice together!
1. A regular pentagon has a side length of 8 cm. What is its perimeter?
We’ve got this one for sure! But let’s go through it just in case.
- Remember, a regular pentagon has equal sides.
- That means that we can do one of two things: we can multiply 8 by 5 to get the perimeter, or we can add 8 together 5 times.
- Let’s multiply: 8 x 5 = 40 cm.
- The perimeter is 40 cm!
2. A regular pentagon has a side length of 6 cm and an apothem of 4.18 cm. Find its area.
Let’s walk through it together, step by step.
- We know we can find the perimeter of a regular pentagon by multiplying 6 by 5. That gives us a perimeter of 30.
- We have an apothem of 4.18 cm. So, then we plug those values into our equation.
1/2 x Perimeter x Apothem sq units
- When we do that, we get: 1/2 x 30 x 4.18 cm = 62.7 square centimeters
3. The apothem of a regular pentagon is 6.96 cm and the length of each side is 10 cm. What is the area of the pentagon?
Easy peasy, right? Let’s walk through it!
- Remember, the formula for finding the area of a regular pentagon is: Area = 1/2 x Perimeter x Apothem
- Let’s find the perimeter. For a regular pentagon, the perimeter (the sum of the lengths of the sides) is simply 5 times the length of one side, because all sides are equal. So, since each side is 10 cm, the perimeter is 5 x 10 cm = 50 cm.
- Apply the formula for the area. We know the apothem is 6.96 cm, and we’ve found the perimeter to be 50 cm. Now, we substitute these values into the formula:
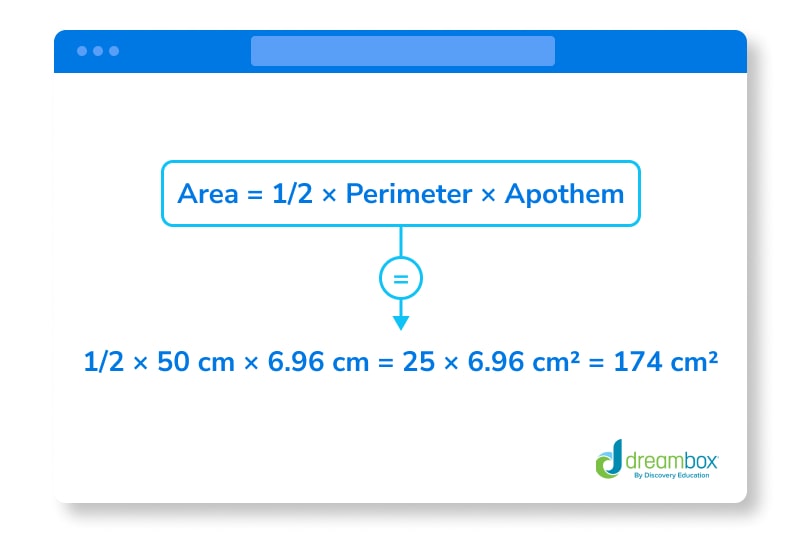
- So, the area of the pentagon is 174 cm².
Ready to give it a go?
- Now that we’ve practiced together, it’s time to try things out on your own! Try the next few practice problems to test your knowledge of pentagons. Don’t be afraid if you get a little lost – just go back through this guide to help you! You’ve got this!
Practice Problems
Click to reveal the answer.
The answer is false.
The answer is 45 cm.
The answer is 250.8 cm².
Parent Guide
-
1. The answer is false. How did we get here?
- Only regular pentagons have five equal sides.
-
2. The answer is 30 cm. How did we get here?
- 1. This is an irregular pentagon, which means we need to add up the measure of all sides of the shape.
2. So we add 4 cm + 5 cm + 6 cm + 7 cm + 8 cm = 30 cm. -
3. The answer is 45 cm. How did we get here?
- 1. We’re dealing with a regular pentagon, which means all sides are equal.
2. That means we can multiply the length of the side by 5 to get the perimeter.
3. 9 × 5 = 45 cm. -
4. The answer is 250.8 cm². How did we get here?
- 1. Since this is a regular pentagon, we can use the formula 1/2 x Perimeter x Apothem to find the area.
2. First, let’s find the perimeter. 12 x 5 = 60 cm.
3. 1/2 x 60 cm x 8.36 cm² = 1/2 x 501.6 cm² = 250.8 cm².
FAQs about pentagons
A pentagon shape is a geometric figure with five straight sides and five angles.
Not always! Only a “regular” pentagon has five equal sides. An “irregular” pentagon has sides of different lengths.
The total degrees of all angles inside any pentagon, whether regular or irregular, is 540 degrees.
A five-sided pentagon is unique because of its five edges. In contrast, triangles have three sides, rectangles have four, and hexagons feature six sides.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


About the Author
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans, while earning a masters degree in business administration.

