What Are Vertices?

Watch it all come together as you master vertices!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield

Published: August 24, 2023

What Are Vertices?

Watch it all come together as you master vertices!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield

Published: August 24, 2023

What Are Vertices?

Watch it all come together as you master vertices!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield

Published: August 24, 2023

Key takeaways

A vertex is the point where two lines intersect – We’ll see them a lot in geometric shapes, such as cubes or pyramids.
There can be more than one vertex in a shape – Multiple vertex points are known as vertices.
Some shapes won’t have vertices – Circles, for example, have no vertices since they do not have any straight lines that come together — which means that there are no intersection points.

Table of contents

Understanding vertices helps you bring shapes to life — giving you a better grasp of geometry, graph applications, and spatial awareness. They show you how objects in your universe appear and can even spice up your next art project with some realistic light-and-shadow placement positions.

We’ll save graph theory and Euler’s formula for another time and keep it super simple by starting with a definition of the term “vertices.”

Vertices are simply points in a shape where lines intersect. You can use vertices n to help calculate the given geometry of sides, angles, and faces in a certain shape. We’ll help you master the skills below, giving you everything you need to walk away with 100% on your next exam.

Solid shapes vs. plane shapes

Before we understand the vertices of all shapes, we must first define a solid shape vs. a plane shape.

Plane shapes are shapes that are two-dimensional which means they appear flat when drawn on paper. Their only elements are length (L) and width (W). Triangles, squares, and rectangles are examples of plane shapes.
Solid shapes are shapes that appear three-dimensional when drawn on paper. Solid shapes include length (L) width (W) and height (H) elements to their construction. Examples of solid shapes include spheres, cubes, and prisms.

What are faces?

Faces are flat surfaces of solid or plane shapes. For example: The flat, wide portion that you see when you draw a rectangle on a piece of paper is considered a “face” of the shape. If you were to make the rectangle a 3D shape and turn it around, as you would with a wooden block toy, you’d see the other faces to the sides, top, and bottom of the shape.

What are edges?

Edges are lines that join vertices (or intersection points). Edges can look different depending on which shape you’re working with, ranging from straight lines to curved lines. Both 2D and 3D shapes can have edges.

Learning how to identify edges in a shape is useful, since they’ll act like the roadmap to your next vertex!

Edges in a 2D shape

It’s simple to spot edges in a 2D shape, since they are lines that join vertices together. In a 2D square, for example, you’ll see four edges going around the perimeter of the shape.

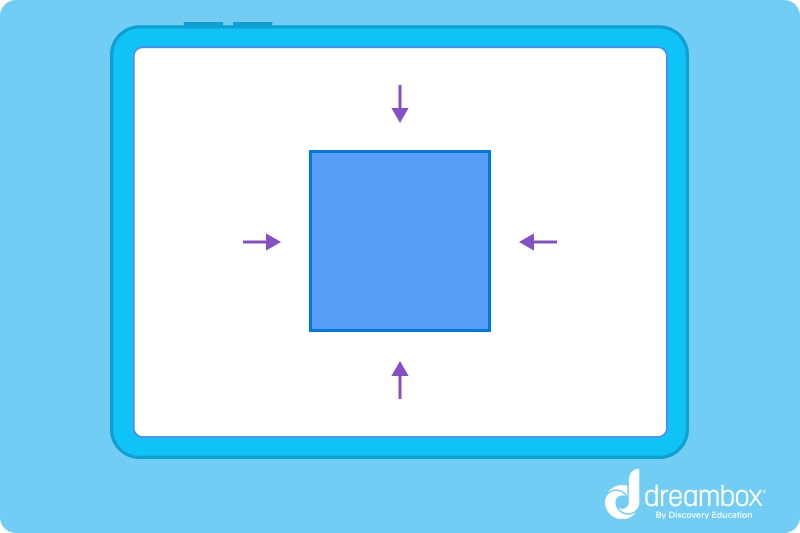
Edges in a 3D shape

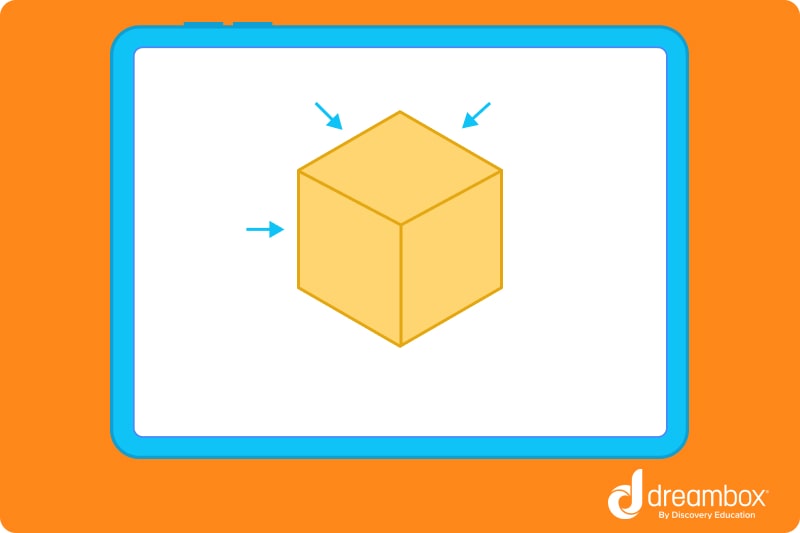
Edges in a 3D shape do essentially the same job that they would in a 2D shape. The only difference here is that they are lines that separate each face on a shape.

Take a wooden block, for example. No matter which way you turn it, you’ll probably see about 3-4 different edges at any time. They separate the block’s “sides,” or faces.

What are vertices?

Vertices, otherwise known as the plural form of a vertex, are points in a shape where lines come together, or, intersect. Knowing where your vertices are in a shape makes it easier for you to calculate angles (as you would in geometry) and to determine what shape you’re working with.

Learning the definition of vertices is the first step to mastering this area of math. Get ready to dive into different examples across both plane and solid shapes.

Difference between edges and vertices

Unlike vertices, edges are never intersection points. Instead, edges act as roads that take you to the vertices.

If you’re ever lost on a shape-related vertex question, always start looking for the end points of “lines” of your shape. This is a helpful first step that can tell you whether the shape has vertices or not.

Unless the shape is a circle or a sphere, you will usually have at least one intersection point.

Let’s explore what vertices look like in the world around us.

Vertices of 2D Shapes

Both two-dimensional (2D) and three-dimensional (3D) shapes can have vertices, so long as there are points in the shape where edges meet.

Square

Squares are 2D shapes that appear flat on paper. They have four vertices, or points of intersection, in their shape. These points are the corners of the square, no matter how small or large a square might be.

Triangle

Triangles are 2D shapes that have three vertices. They are clearly seen as the corners of the shape, no matter what size triangle you’re working with.

Rectangle

A rectangle is a 2D shape that has four vertices, each located at the rectangle’s corners. These vertices, or intersection points, are always present (no matter how large or small the rectangle is).

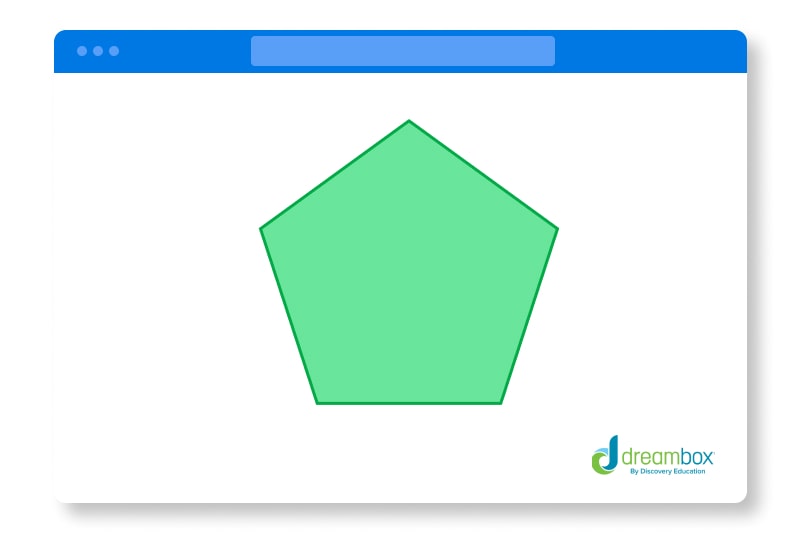
Pentagon

A pentagon is a five-sided, 2D shape that has five vertices — which can be seen at each corner of the shape — no matter what size the pentagon.

Have you noticed a pattern yet? Regular shapes have the same number of vertices as their number of edges!

Irregular shape

Irregular shapes, by definition, have many different sides and angles that are different lengths and sizes.

If you’re trying to see if an irregular shape has a vertex (or vertices), take a look to see if there are any intersection points between lines. If there are, your shape has at least one vertex.

Circle

A circle is a 2D shape that features one line that curves — forever. Since it only is made of one curved line, however, it cannot (and will not) ever have a vertex point.

Vertices of 3D shapes

Now that we know the average number of vertices in several “normal” 2D shapes, it’s time to take a look at vertices in 3D shapes.

Our understanding of a vertex doesn’t change — a vertex is still where lines or edges meet — only it just might look a little different in 3D shapes (like a triangular prism!)

Cube

A cube is a 3D shape that you’ve probably seen before (think like a moving box!) It has 8 vertices, or intersection points, in its construction.

Prism

A prism isn’t so much a shape as it is a group of shapes. To be a prism, a shape has to be 3D with flat sides. At least two of these sides have to be the same shape and size, and when cut, it must be symmetrical. A prism also cannot have a curve.

Since a circle cannot be a prism (since prisms have no curves), prisms always have vertices. There are many types of prisms, including:

Pentagonal (or pentagon-shaped)
Rectangular
Square
Polygonal (or polygon-shaped)

To find the number of vertices in a prism, count the number of vertices on the base face, then multiply by 2. For example, for a pentagonal prism, the pentagon will be its base-face. So, count the number of vertices on a pentagon (5), then multiply by two since there is another face on the opposite side of the prism that is a pentagon too. So, the number of vertices on a pentagonal prism is 10.

Cuboid

A cuboid is a lot like a cube — the only difference is it has rectangular “faces” (or surfaces) instead of perfectly square ones like you’d see in a true cube! Like a cube, cuboids always have eight vertices (or intersection points), no matter how short or tall their faces appear to be.

Cone

A cone is a 3D shape that you’re probably familiar with if you’ve ever had a sweet, cold ice cream cone!

This familiar shape only has 1 vertex — and it’s right at the tip, or the narrowest point.

Cylinder

If you’ve ever seen a can of green beans or corn, you’ve seen a cylinder! A cylinder is a shape which features two flat circle-style faces on each end and a single curved surface.

While there are technically two vertical “edges” to the shape, there are no intersection points since these edges are curved. This means that cylinders do not have vertices, as no edges meet at a corner in the shape.

Sphere

A sphere is a ball — and 3D balls do not have any points of intersection. This means that spheres do not (and will not) have vertices in their construction.

👉 Fun fact: Spheres and circles are not the same shapes. Spheres are solid, three-dimensional figures in which no faces meet. This is because the shape has no faces at all — it is simply round. This means the rules and applications for vertices or related properties won’t work with spheres.

Let’s practice together!

1. How many vertices does this shape have?

First, we find out what shape we’re working with. This example is using a square.
We then follow the edges of the shape to find any possible intersection points. In this shape, there are four intersection points. We only have to check the single face provided, since it’s a 2D shape.
We write 4 as our answer.

2. How many vertices does this shape have?

First, we find out what shape we’re working with. This example is using a cuboid. (We know this isn’t a true cube, since the shape’s face appears to be more rectangular than a true cube would).
We then follow the edges of the shape to find any possible intersection points. In this shape, there are eight. We check all possible faces, as this is a 3D shape.
We write 8 as our answer.

3. How many vertices does this shape have?

First, we find out what shape we’re working with. This example is using a cylinder.
We then follow the edges of the shape to find any possible intersection points. In this shape, it might look like there are vertices. However, they aren’t true points of intersection, since the two circular faces never meet. The lines only connect the faces around the curved surface of the shape.
With this in mind, we remember that cylinders, circles, and spheres (by definition!) do not have vertices.
We write 0 as our answer.

Ready to give it a go?

Alrighty! We’ve given you everything you need to know to successfully find, work through, and answer vertex math problems — now it’s your turn to put it into practice. We know you’ll do great. Just do your best, and don’t be afraid to make mistakes. It’s how you learn.

Try these practice problems to perfect your vertex-identification skills. Show us what you’ve got!

Practice problems

Click to reveal the answer.

1. Find the vertices in the shape below.

The answer is 4.

2. Find the vertices in the shape below.

The answer is 4.

3. Find the vertices in the shape below.

The answer is 8.

4. Find the vertices in the shape below.

The answer is 0.

5. Find the vertices in the shape below.

The answer is 1.

Parent Guide

The answer is line 4.

How did we get here?

First, we find out what shape we’re working with. This example is using a diamond.
We then follow the edges of the shape to find any possible intersection points. In this shape, there are four. We only have to check the single face provided, since it’s a 2D shape.
We write 4 as our answer.

The answer is 4.

How did we get here?

First, we find out what shape we’re working with. This example is using a rectangle.
We then follow the edges of the shape to find any possible intersection points. In this shape, there are four. We only have to check the single face of the shape provided, since it’s a 2D shape.
We write 4 as our answer.

The answer is 8.

How did we get here?

First, we find out what shape we’re working with. This example is using a cube.
We then follow the edges of the shape to find any possible intersection points. In this shape, there are 8. We have to check all faces of the shape provided, since it’s a 3D shape. As we do this, we can confirm that there are no other intersection points.
We write 8 as our answer.

The answer is 0.

How did we get here?

First, we find out what shape we’re working with. This example is using a circle.
We then follow the edges of the shape to find any possible intersection points (there aren’t any, as this is a 2D circle).
With this in mind, we remember that cylinders, circles, and spheres do not have vertices by definition.
We write 0 as our answer.

The answer is 1.

How did we get here?

First, we find out what shape we’re working with. This example is using an irregular, teardrop shape.
We then follow the edges of the shape to find any possible intersection points. On this shape, there is just one, at the tip. We only have to check the single face of the shape provided, since it’s a 2D shape.
We write 1 as our answer.

Turn math into an adventure when you sign up for DoodleMath.

Click here to get started for free!

FAQs about math strategies for kids

We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!

Does the term “vertices” mean edges?

No, vertices are not the same as edges. Vertices are intersection points on a given shape or figure, while edges are the lines that bring faces of a shape together. Edges are unique because they can also lead to vertices in a shape.

Does the term “vertices” mean sides?

No, vertices are not the same as sides of a shape. Shape “sides” in a 2D shape refer to its edges. In a 3D shape, “sides” are more equivalent to faces. Vertices are simply intersection points of a shape, and are generally where two lines meet.

Are points and vertices the same thing?

Points are not the same thing as vertices. A point can be anywhere in a space, while a vertex is a specific term given to intersection points in a given shape. A vertex is a point, but a point is not always a vertex.

What is the difference between vertices and vertex?

A vertex is a term given to a single point of intersection. The term “vertices” means that there are several points of intersection in a given shape or figure.