Menu
Author
Taylor Hartley
Expert Reviewer
Jill Padfield
Published: August 24, 2023
Subtraction is one of the most important math skills you’ll ever learn. Discover all of the different ways to find the difference.
Author
Taylor Hartley
Expert Reviewer
Jill Padfield
Published: August 24, 2023
Subtraction is one of the most important math skills you’ll ever learn. Discover all of the different ways to find the difference.
Author
Taylor Hartley
Expert Reviewer
Jill Padfield
Published: August 24, 2023
Key takeaways
Finding the difference, or subtracting, is one of the most important yet basic concepts in math. Without this skill, it will be almost impossible to move on to more complicated math concepts like multiplying and dividing. Plus, you’ll want to master the basics of subtraction before you venture into subtracting fractions and decimals — heads up 4th and 5th graders! Let’s dig in to learn more about the difference in math.
If you have already mastered finding the sum, learning how to find the difference in math will be a breeze! The difference in math is what you get when you subtract two numbers. Basically, it just tells us how much one number differs from another number — and it’s an important skill to practice. Before we dive in, let’s cover a few key elements that will help us find the difference.
The math symbol for the difference is expressed as a minus sign (-). If you see an equation like this: 10 – 2 = 8, the 10 is called the minuend, the 2 is called the subtrahend, and the 8 is called the difference.
There are plenty of ways to find the difference in math. Finding the method that works best for you is key! Some people are visual learners and prefer to use a number line, while others like to stack the equation vertically and use the borrowing method — both get you to the same place!
Let’s explore the different ways that you can find the difference between two numbers.
One way to find the difference in math is to use a number line — it’s a great visual aid and very easy to learn. For this method, locate the minuend, or the first number in the equation, on the number line and move left on the number line until you land on the subtrahend, or the second number in the equation. While you’re moving left, simply count the amount of hops you made to get to the subtrahend.
The first step to finding the difference with borrowing is to place the values, or numbers, vertically in the order of their place values. You’ll also want to make sure that the greater number is on top and the smaller number is on the bottom. Next, you’ll start subtracting the numbers, starting from the ones place.
If you’re asked to find the difference between 7,869 and 4,684, your equation when using the borrowing method should be set up like this:
In this case, some digits in the subtrahend are greater at a certain place value than the corresponding number in the minuend — but that’s okay! To find the difference, start by subtracting 4 from 9 to get 5. The subtrahend was not greater than the minuend in this place value, so you can move on.
Next, find the difference between 6 and 8. Here, the subtrahend is bigger than the minuend, so you’ll need to borrow! Borrow 1 from the digit that is at the 100s place in the minuend, making it a 7 instead of an 8. Now, the number in the 10s place, the 6, becomes a 16. You can now easily find the difference between 16 and 8 which is 8!
Now, move to the 100s place and find the difference between our new 7 and 6. The difference is just 1. Lastly, find the difference between 7 and 4. The answer is 3. The difference between 7,869 and 4,684 is 3,185. If there are multiple minuend digits that are greater than their corresponding subtrahend digits, simply repeat the borrowing process, always taking one number from the digit to the left and adding a 1 in front of the minuend number you’re working with. It’s important to note that you’re not adding 1, but putting the number 1 in front of the minuend digit. So in this example, the 6 became a 16, not a 7.
Again here, the first step to finding the difference without borrowing is to place the values, or numbers, vertically in the order of their place values. You’ll also want to make sure that the first number is on top and the number you are subtracting is on the bottom of the equation. Next, you’ll start subtracting the numbers, starting from the ones place.
If you’re asked to find the difference between 7,869 and 3,653, your equation when you’re not borrowing should be set up like this:
We can see that each digit in the subtrahend is less than its corresponding digit in the minuend, so we can do simple subtraction to find the difference! The difference between 9 and 3 is 6, between 6 and 5 is 1, between 8 and 6 is 2, and between 7 and 3 is 4. So, the difference between 7,869 and 3,653 is 4,216.
You might have already guessed it, but there are so many more advanced applications and methods to finding the difference in math. For now, we’ll give brief examples of how to find the difference between two fractions and decimals to get you familiar, but you probably won’t need to use these skills until 4th and 5th grade!
To find the difference between two fractions, there are a few steps you have to follow:
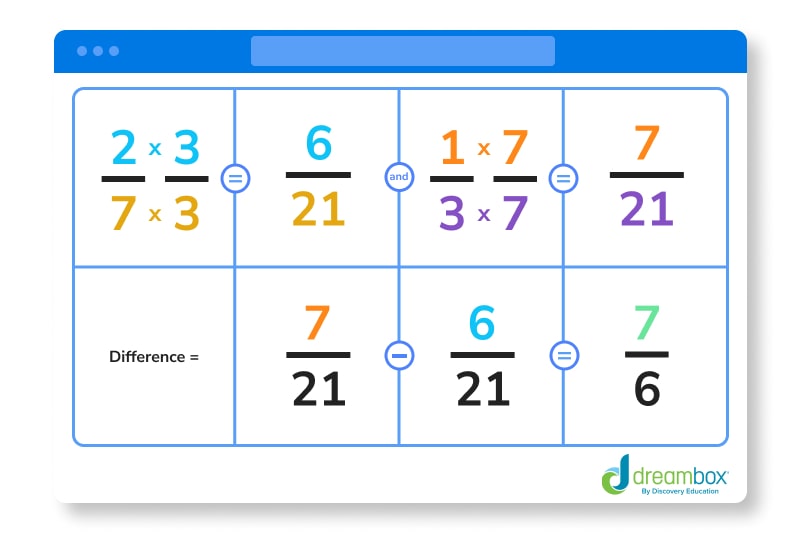
Phew — okay, now it’s time for an example! If a recipe calls for ⅓ sugar and 2⁄7 milk, how much more sugar is there compared to milk?
First, we know that the fraction that symbolizes sugar = 1⁄3
Second, we know that the fraction that symbolizes milk = 2⁄7
The LCM of 3 and 7 is 21.
To find the difference between two decimal numbers, there are a few steps that you have to follow:
Ready for another quick example? And don’t worry if it’s a bit confusing to start — again, this will be more thoroughly explained in 4th and 5th grade!
Let’s find the difference between 39.03 and 8.762.
We will first need to convert both the decimal numbers into like decimals by adding one zero in 39.03. So, it can now be written as 39.030.
Next, subtract them like whole numbers, borrowing when needed, and place a decimal point. The difference is 30.268.
Need to run through a few more problems on your own? Keep practicing!
Ready to give it a go?
Now that we know how to find the difference using multiple different methods, we’re ready to do a few more practice problems to put these new skills to the test! Work through the following problems on your own. Feel free to look back at the practice problems above if you get stuck, or if you need a quick reminder on how to find the difference.
And remember, don’t get discouraged if you run into a roadblock! Practice is the best way to learn something new.
Click to reveal the answer.
The answer is 5.
The answer is 6.
The answer is 357.
The answer is 18.
The answer is 5.
How did we get here?
B is incorrect.
How did we get here?
The answer is 6.
How did we get here?
The answer is 357.
How did we get here?
The answer is 18.
How did we get here?
Sign up for the DoodleMath app today!
Turn math into an adventure when you sign up for DoodleMath.
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
In math, the term “difference” refers to the result of subtracting one number from another. It indicates the numerical gap or distance between two quantities. On the other hand, “sum” refers to the result of adding two or more numbers together.
To find the difference between two numbers, subtract the smaller number from the larger number. The result will be the numerical gap or difference between the two values.
Regrouping, also known as borrowing or renaming, is a technique used in subtraction when the digit being subtracted from is smaller than the digit being subtracted. It allows us to perform the necessary subtraction by “borrowing” or regrouping from the next higher place value.
Subtraction is going to be absolutely crucial as you climb up the mountain of mathematical knowledge! It provides us with a way to calculate differences, solve problems, analyze data, establish relationships, and work with algebraic expressions.
Title 1
Helpful description
Read now
Title 2
Helpful description
Read now
Title 3
Helpful description
Read now
Lesson credits
Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Parents, sign up for a DoodleMath subscription and see your child become a math wizard!
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
