

Area models are visual aids used to make multiplication and division problems simple.

Author
Amber Watkins
Published
November 6, 2023


Area models are visual aids used to make multiplication and division problems simple.

Author
Amber Watkins
Published
Nov 6, 2023


Area models are visual aids used to make multiplication and division problems simple.

Author
Amber Watkins
Published
Nov 6, 2023


Key takeaways
Table of contents
Area models are visual aids used to make multiplication and division problems simple.
With area models, your child can:
1. Multiply two and three-digit numbers.
2. Divide two and three-digit numbers.
3. Multiply fractions and decimals.
First, let’s look at the big picture to see what area models look like and to understand the similarities between finding area and using area models, then we will see how they can be used to solve problems.
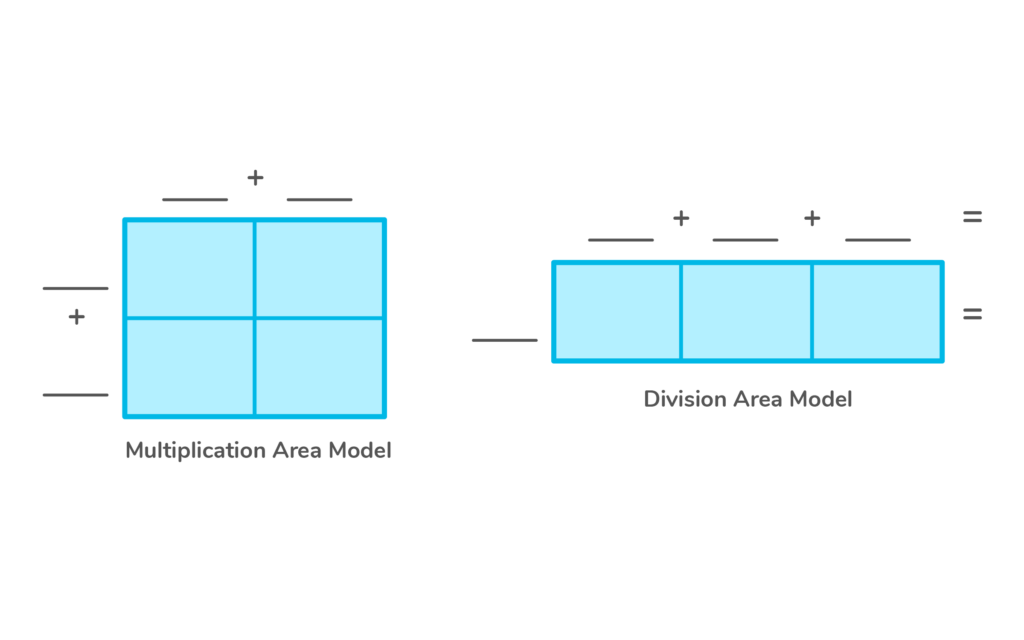
When you look at an area model, they are drawn as a square or a rectangle.
Fun Fact: Area models in square shape are called “square models.”
Since there are many similarities between finding the area of a square or rectangle and using these models to multiply or divide, they are called area models.
How do you find the area of a rectangle? Multiply the length times the width.
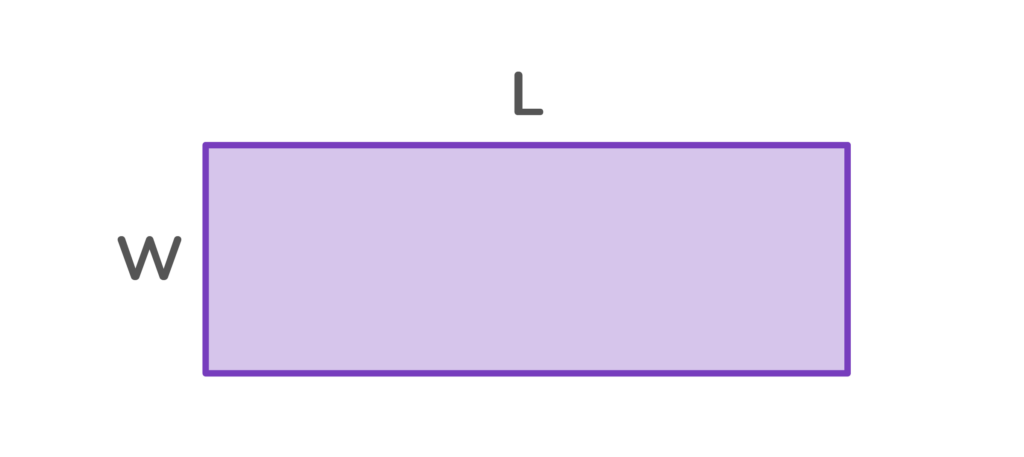
When using area models to multiply, one number is used as the length; the other number is used as the width.
Area models help you to find the area in parts which makes the problem easier to solve.
What if you are given the area of a rectangle, but are missing a measurement for one of the sides? You divide the area by the side length.
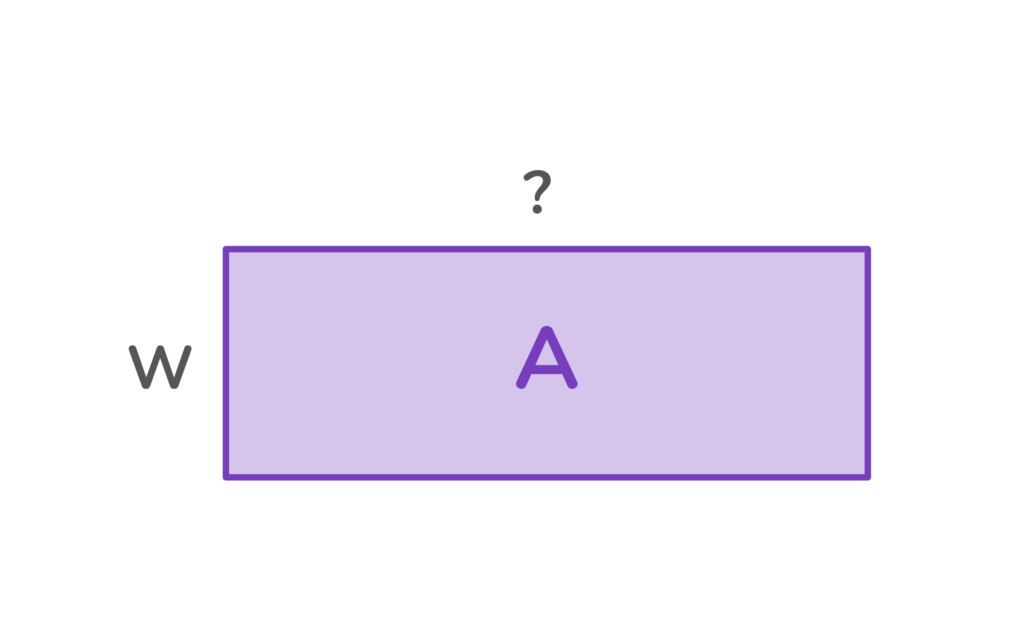
When dividing using area models, the dividend is the area, and the divisor is the length of one of the sides.
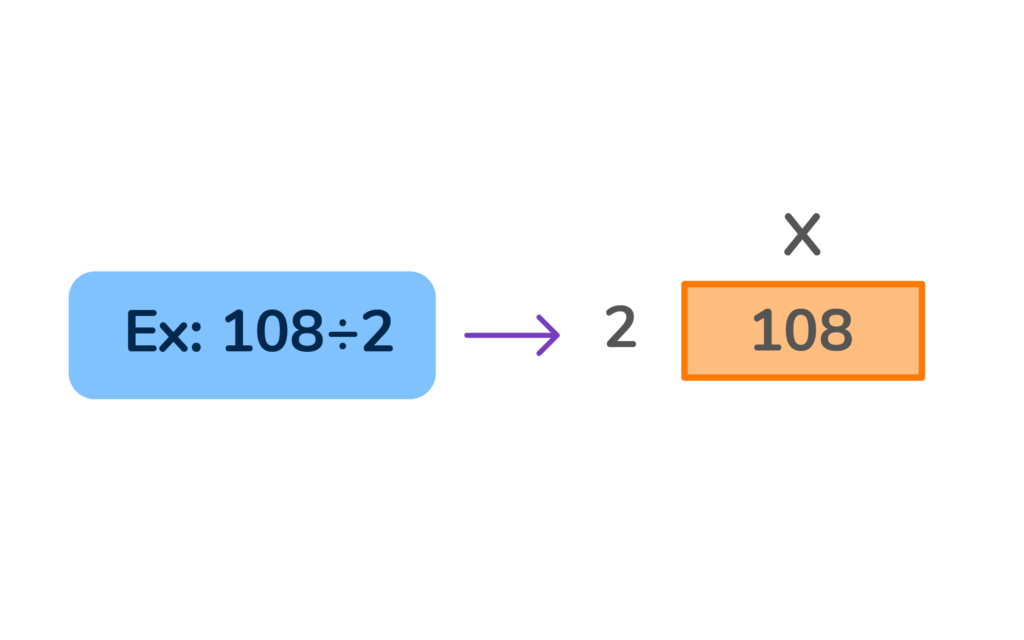
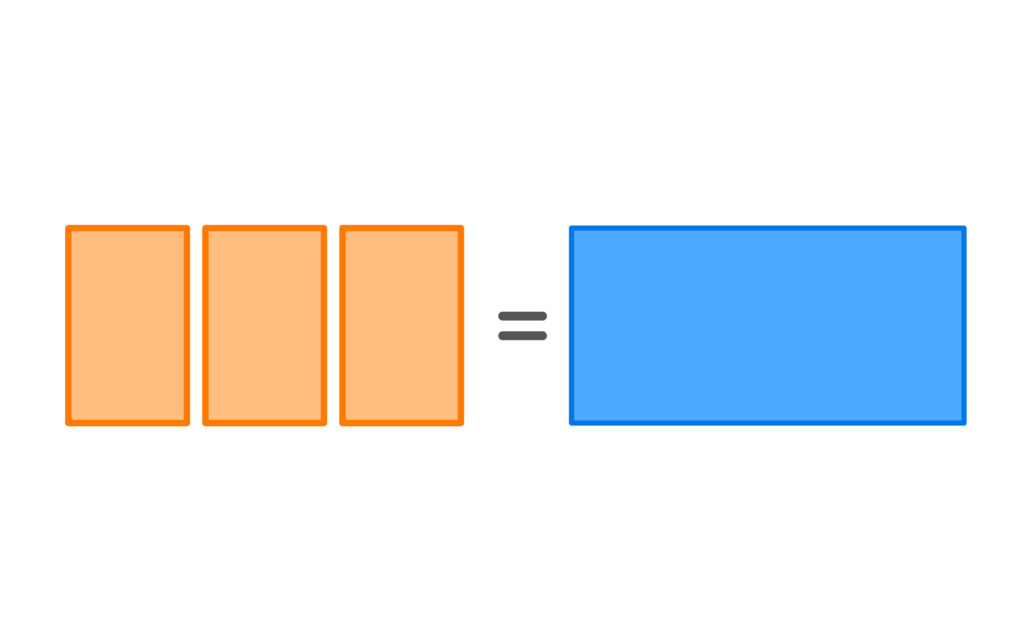
Area models help us divide the area into parts which makes finding the missing length easier.
Let’s see how to solve an area model multiplication problem.
What is 25 x 42?
We are going to use this multiplication area model to find the answer in parts.


3. Now we have the numbers needed to multiply. Take each box and multiply the number above the column by the number before the row. (See the detailed illustration below).
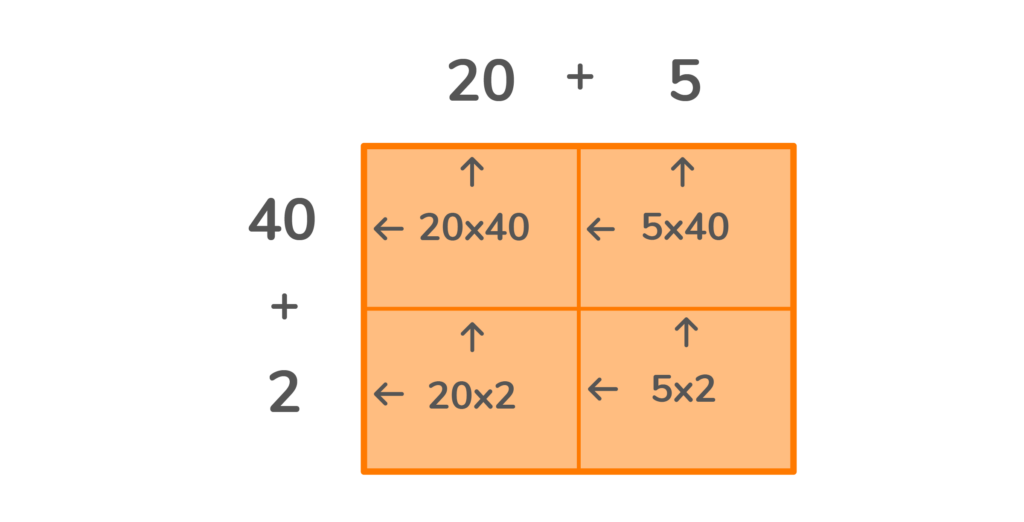
You will end up with one number in each of the four boxes.
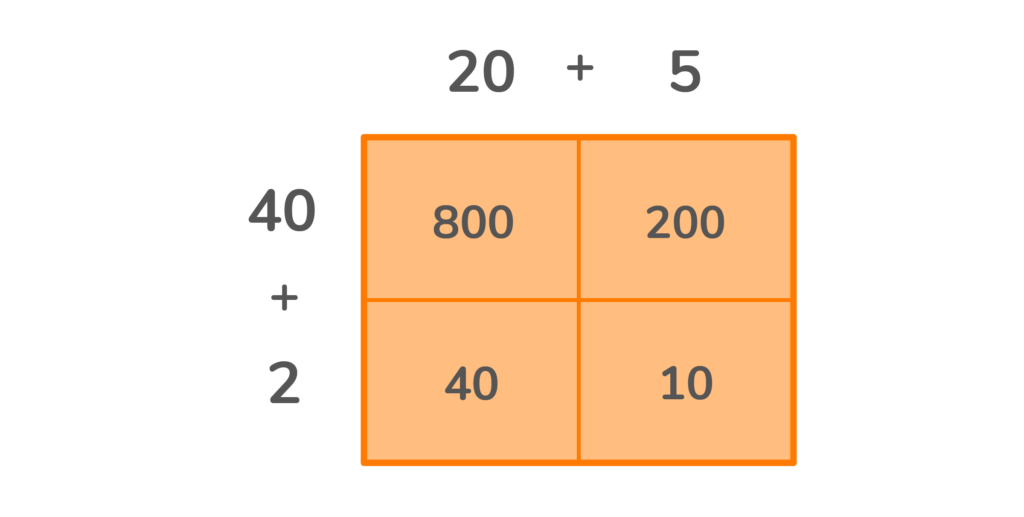
4. The final step is adding all the numbers together to find the answer.
800 + 200 + 40 + 10 = 1,050. So, 25 x 42 is equal to 1,050.
Let’s see how to solve an area model division problem.
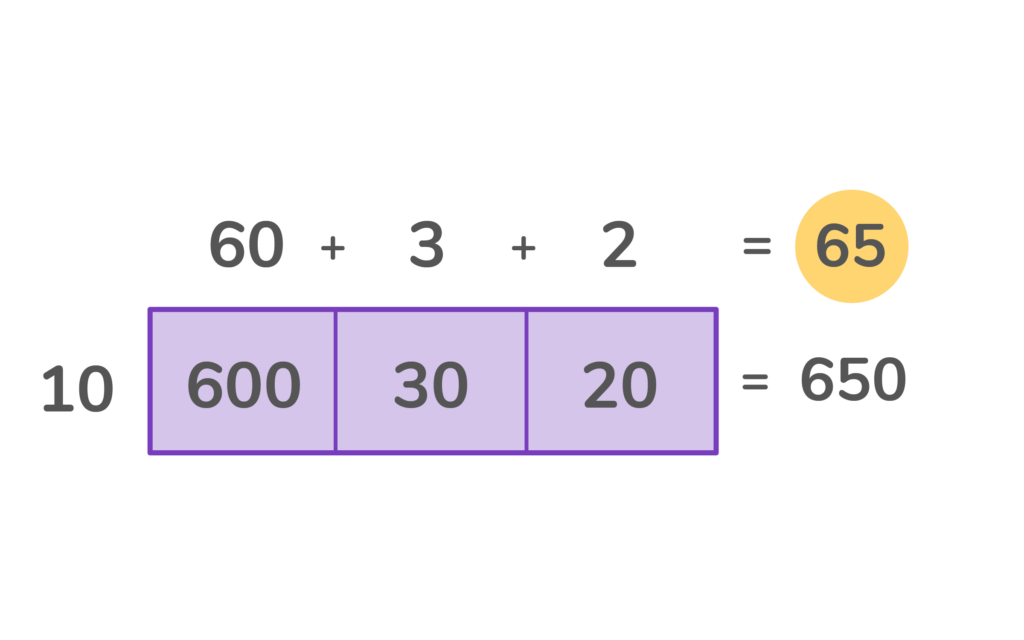
What is 650 / 10 =
We are going to use this division area model to find the answer in parts.
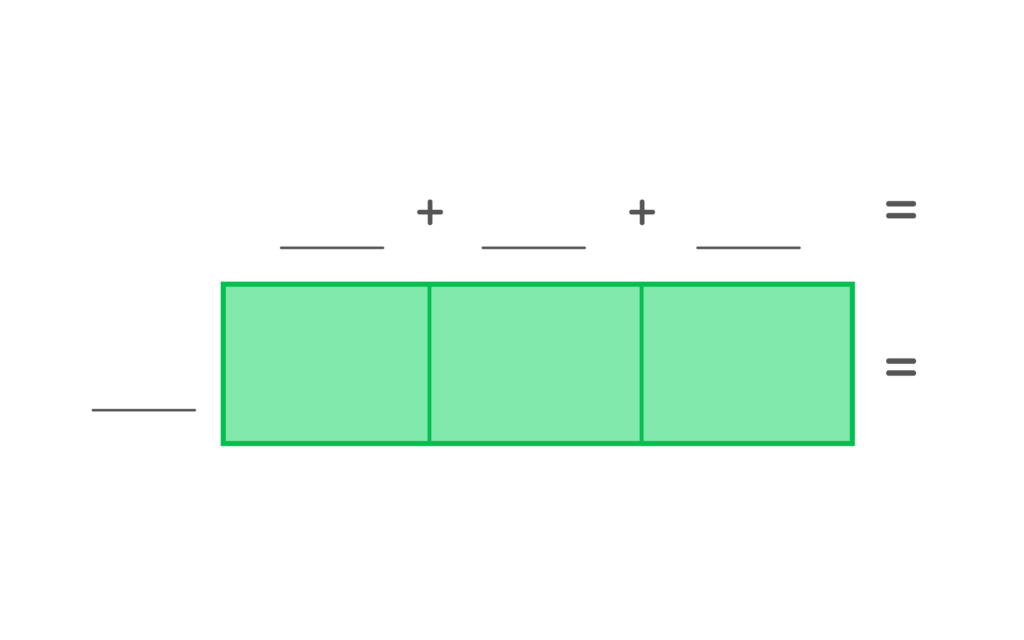

2. Choose three numbers that can be added to equal 650, 600 + 30 + 20. Place those three numbers inside the area model. Hint- all three numbers should be divisible by 10, the divisor.
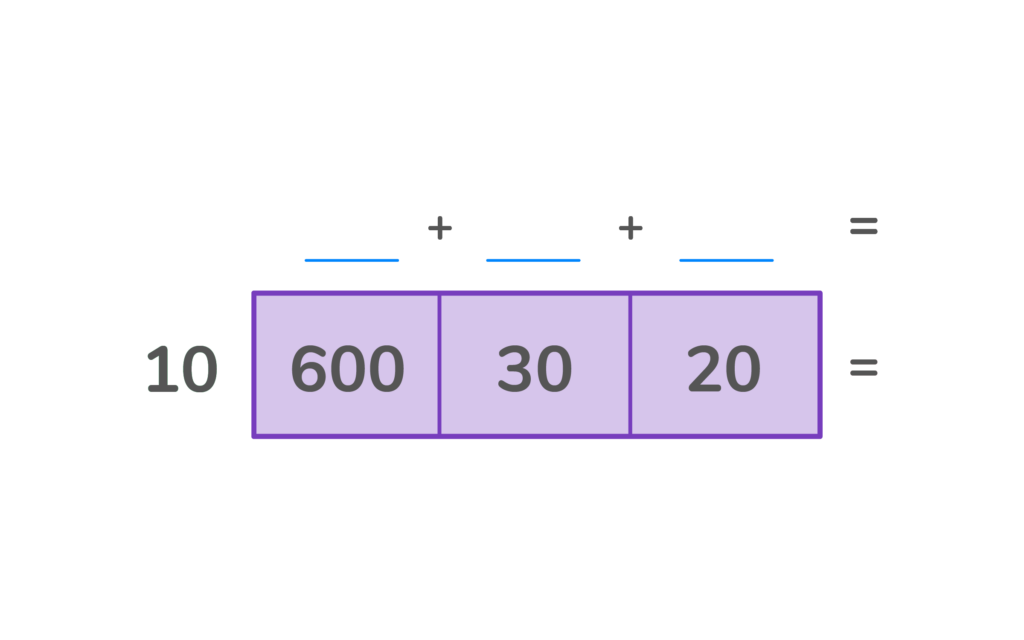
You will end up with one number in each of the four boxes.
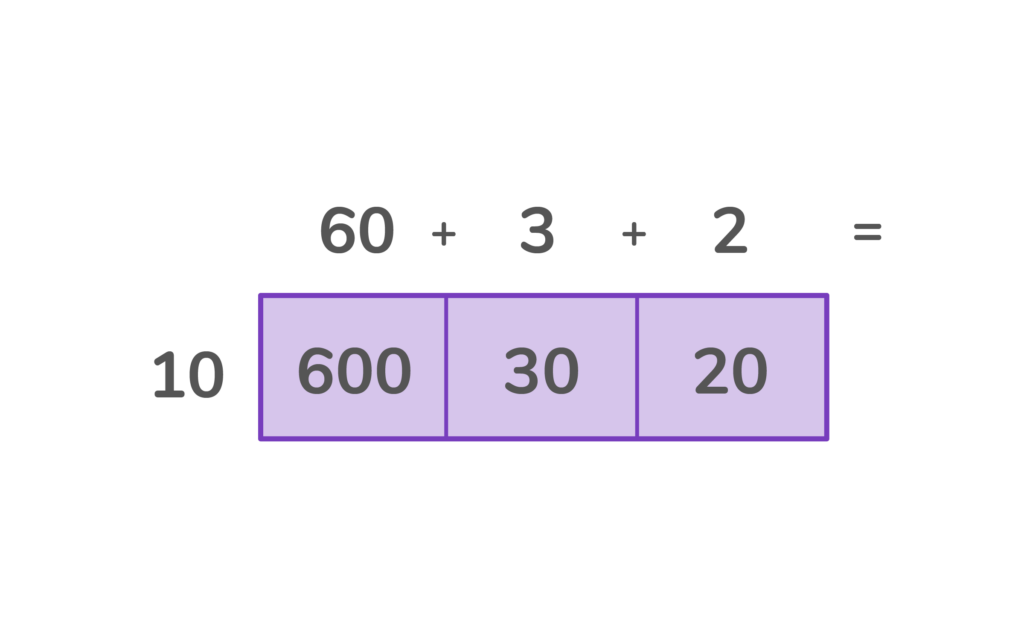
4. Finally, add the top numbers to find the missing length.
1. Using the multiplication area model, find the product of 62 x 13 =
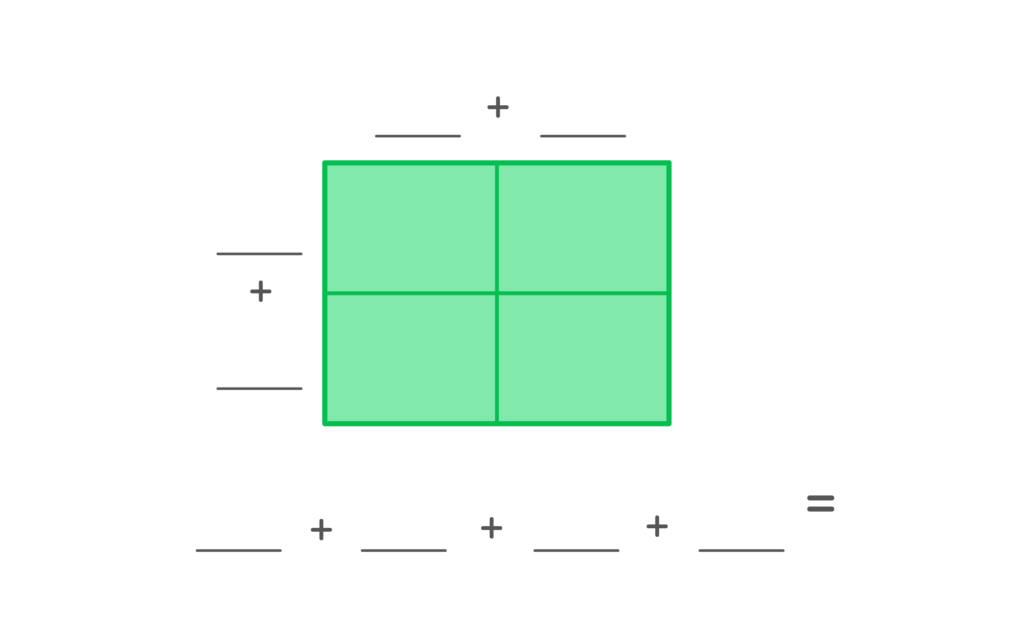
2. Using the multiplication area model, find the product of 4.9 x 3.5 =
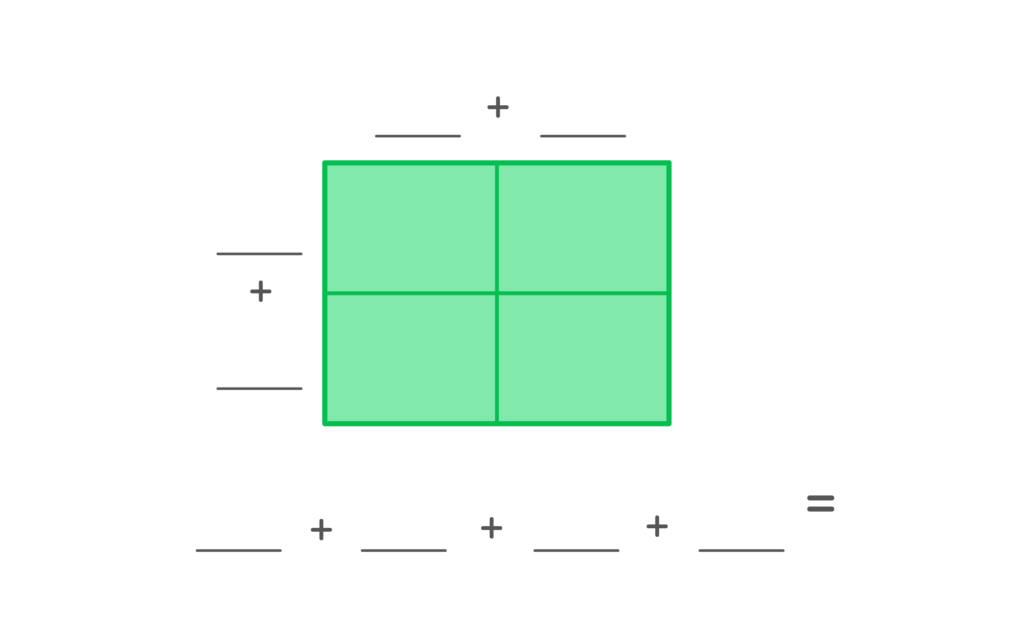
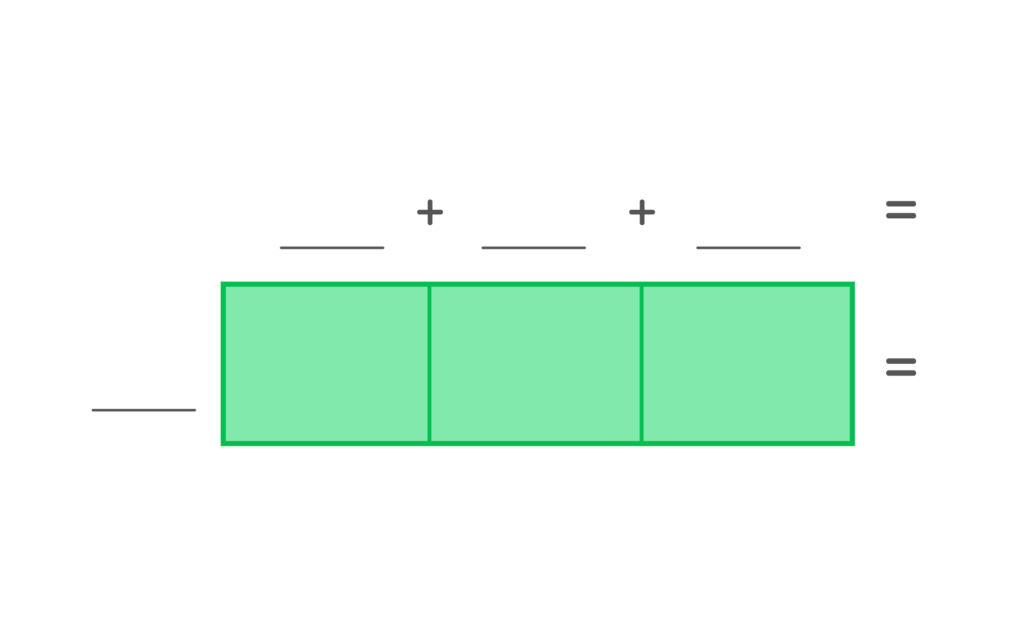
3. Using the division area model, find the quotient of 180 / 12 =
1. 62 x 13 = 806
2. 4.9 x 3.5 = 17.15
3. 180 / 12 = 15
Square models are area models used to multiply two-digit numbers.
Area models help you find the area in parts, this makes the problems easier to solve.

Lesson credits

Amber Watkins
Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring elementary through college level math. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"

Amber Watkins
Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring elementary through college level math. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"

Parents, sign up for a DoodleMath subscription and see your child become a math wizard!

Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: