Some knowledge and practice will quickly add up as you learn the ins and outs of addition!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: September 1, 2023


Some knowledge and practice will quickly add up as you learn the ins and outs of addition!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: September 22nd, 2023




Some knowledge and practice will quickly add up as you learn the ins and outs of addition!

Author
Taylor Hartley

Expert reviewer
Jill Padfield
Published: September 22nd, 2023


Key takeaways
Aside from simple counting, addition is the most basic and fundamental mathematical skill you can learn. Before you can subtract, multiply and divide, you need to be able to combine numbers together through the power of addition.
Addition is a handy skill that most people use daily, whether when cooking a meal, scheduling different activities or figuring out how many sweets they’ve eaten in a day!
No matter how much maths you plan on doing in your life, make no mistake: everyone needs to know addition! Let’s take a deeper dive into this valuable skill.
There are a few options to help you find the sum of numbers. Depending on how your mind works, some of these options will make more sense than others. Feel free to try them all out and see what works best for you!
Let’s get started looking at how to find the sum of two numbers. We’ll keep things simple for now.
A number line is a simple visual representation of numbers counting from 1 to whatever value you’d like. An easy way to figure out a sum is to use a number line.
Start by looking at your addition problem. Let’s look back at the example from earlier, 5 + 7. Look at the first number in the problem, 5, and count that many spaces on the number line. You’re halfway done already!
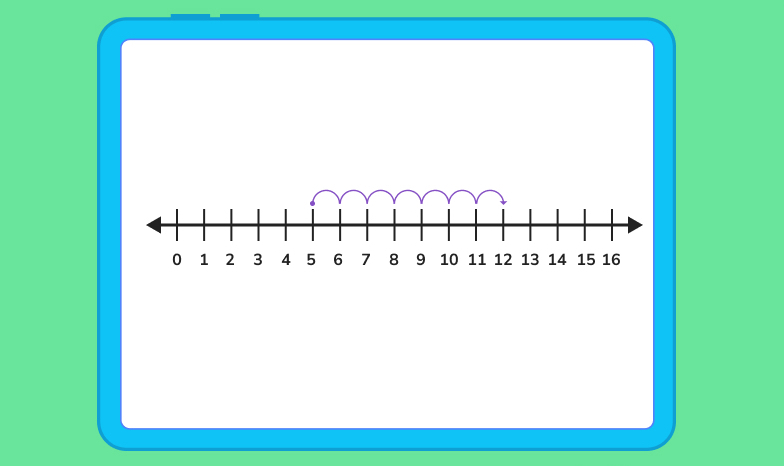
Now, look at the second number in the problem, which is 7. Keeping your place on the number line that you found with the first number, count out 7 more spaces on the line. 5, 6, 7… all the way to 12!
Guess what? You just found the sum of 5 and 7!
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Want to have a go at some questions? DoodleMaths is an app that’s filled with fun games and exercises all about addition, as well as subtracting, dividing and more!
Created by teachers, it’s fully aligned to the KS1 maths curriculum and breaks down learning into small, bitesize chunks, building a solid foundation of understanding.
Best of all, it rewards effort over ability and is filled with interactive topic explanations, letting your child work independently. Try it for free today!

If you’re trying to find the sum of smaller numbers and you don’t have any paper handy for a number line, you can use your fingers!
Let’s do this with a new addition problem, 3 + 6.
Start with your hands balled up into fists. As you count out the numbers, you’ll hold up fingers to help you keep track, just like with spaces on a number line.
Hold out your left hand. We’re going to start with the first number again, which is 3. Count it out — 1, 2, 3 fingers.
Great, now let’s handle that second number, 6. On the left hand, keep those 3 fingers up but start counting to 6 using the fingers you haven’t raised yet.
1… 2…
Now all the fingers on your left hand should be up. But wait, you’re all out of fingers! Well, you can move onto your right hand.
Keep counting. You can get all the way to 6 by using the 2 fingers you had on your left hand and 4 on your right. Now, count how many fingers you are holding up. You should see 9 fingers total, which is the sum of 3 and 6!
For sums greater than 10, you will need to ‘carry’ the one mentally and start over by lowering your fingers. We’ll talk more about ‘carrying’ in the next section.
Eventually, you’ll need to start adding up larger and larger numbers. That means eventually the number line will get a little too long, and you’ll quickly run out of fingers (and toes!) for counting.
You’ll need to rely on regrouping or carrying numbers to handle larger addition problems.
Let’s say you need to find the sum of 24 and 32. Things are about to get a little tricky, so let’s try to arrange these numbers to make things easier to understand.
We’ll stack them up on top of each other so we can handle one part of each number at a time. It will look like this:

Notice how the larger number is on top. It doesn’t matter which number goes on top in addition, but putting the larger number up there is a good habit to get into because of how things like subtraction work. We’ll worry about that later, though.
Now that we have the numbers lined up, we’re going to add one column at a time, starting with the ones place.
Let’s start by adding 2 and 4 together. For this you can try using the number line or your fingers again.
2 + 4 = 6, so let’s write a 6 down below the 2 and the 4. Like this:
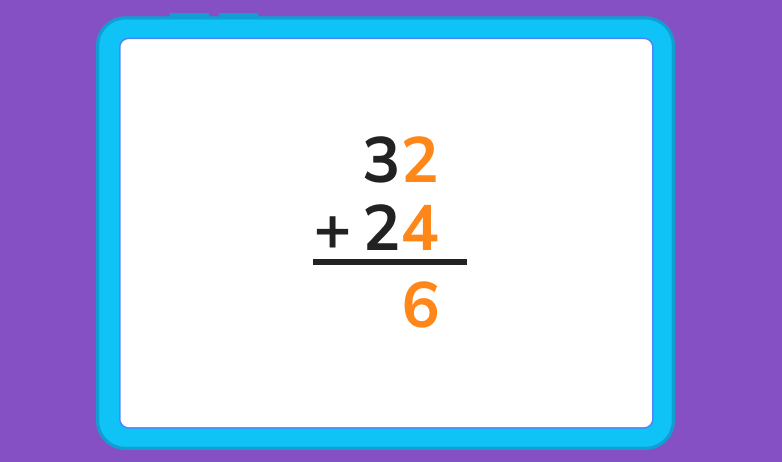
Drawing a line between the numbers you’re adding and the sum you’re working on will help you keep the numbers straight.
Now that we’ve added the numbers in the ones place, let’s move onto the tens.
Add up 3 and 2 with your number line or fingers and write it below in the tens space next to the 6.
3 + 2 = 5, so let’s drop that down below:

And there you have it! 32 plus 24 equals 56.
It does get a little more complicated sometimes, though.
Take a look at this problem next. What is 27 + 15?
Let’s set that up just like before:

Just like before, we’ll start with the ones place. 7 + 5. That will get you to 12, but here’s the problem.
You can’t just write 12 down below like you did with the 6 from the last problem because that would take up the spot where you would add the 2 and the 1 in the tens place, right?
What you have to do is ‘carry’ the 1 in the 12 you got from adding 7 and 5.
That ‘1’ in the number is basically just 10. You can think of 12 as being 10 + 2. That means you can put the 2 below just like before, and move the 1 to above the 27.
It’s easier to see it in action:

Remember that the 1 up there is basically just a 10, so you’re adding 3 numbers now, but it’s nothing you can’t handle.
Let’s add up those numbers in the tens spot now. 1 + 2 + 1. 1 + 2 will get you 3, and then you add 1 to that to get 4.
Let’s write that down below:

And there you have it! 27 plus 15 equals 42.
You can use the ‘carrying’ technique as many times as you need to in an addition problem. Any time a column adds up to more than 9, you’ll carry the 1 in the tens place and place it over the next column.
Here’s an example of this process going into the hundreds place:

Add up the numbers in the ones first. 7 + 5 = 12, so the 1 is carried.
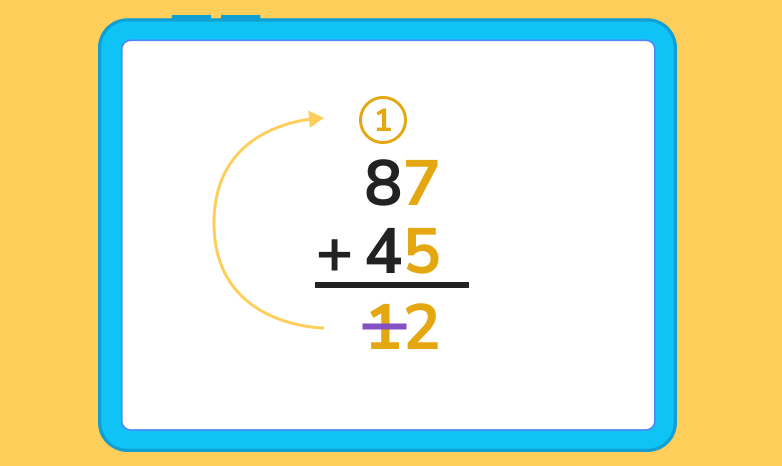
Time to add up the numbers in the tens place:
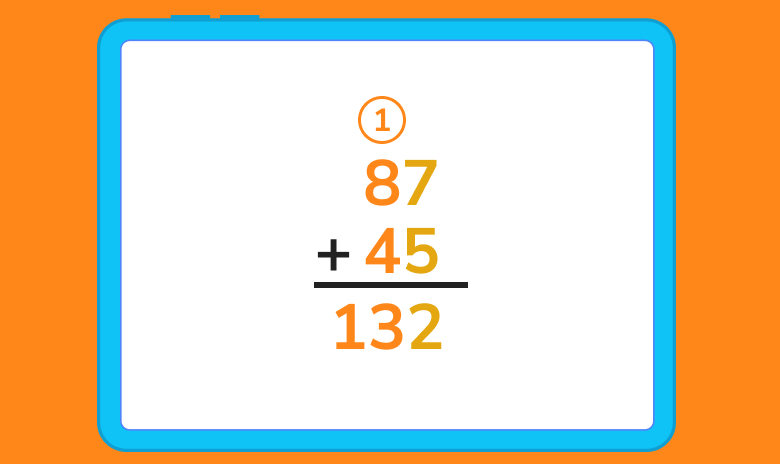
Note that if you were adding up numbers that had hundreds, you would need to carry the 1 again until you run out of columns.

As you might expect, addition can get even more complex since there are so many different things you can add.
Fortunately, you won’t have to worry about more complicated addition until later in school, but it’s good to start thinking about these ideas!
When it comes to things like cooking and baking, with 1/2 a teaspoon here and 1/2 a tablespoon there, you’ll need to figure out how to add fractions together – otherwise, your chocolate cake might turn into a gooey chocolate fondue!
To find the sum of two fractions, there are a few steps you have to follow:
Let’s take a look at this in action! If a recipe calls for 1/2 a tablespoon of sugar and 2/3 of a tablespoon of flour, how many tablespoons do you need in total?
First, we know that the fraction for sugar = 1/2
Second, we know that the fraction for flour = 2/3
So we’re trying to find out 1/2 + 2/3 = ?
The LCD of 3 and 2 is 6. How do we know this? Well, for this part, you need to know some multiplication, which is a skill you will learn more about later, but just in case you are a little ahead, here’s what that looks like:

To find the LCD, multiply the two denominators together. You’ll also need to multiply the numerators (the numbers on top) by the denominators.
There you have it! 1/2 + 2/3 = 7/6
To find the sum of two decimal numbers, there are a few steps you have to follow:
Time to see this in action, too!
Let’s find the sum of 2.36 and 6.721.
We’ll first need to convert both the decimal numbers into like decimals by adding zeros to fill in the missing places so that each number has the same number of digits behind the decimal.
6.721 has 3 digits behind the decimal, but 2.36 only has 2. Just add some zeros to make them even, which will make 2.36 into 2.360. This doesn’t change how much the number is, but it’ll make adding much easier.
Next, add them like whole numbers, moving from right to left, carrying the 1 if and when needed. Don’t forget to put the decimal in your answer!

The total is 9.081!
Ready to give it a go?
Now that we know how to find the sum of multiple numbers using different methods, we’re ready to put these new skills to the test!
Work through the following problems on your own. Feel free to look back at the practice problems if you get stuck or need a reminder on how to find the sum.
You may find some of the more advanced problems a bit tricky, but don’t worry! Remember the basics, pay attention to the little details and keep on practicing.
Click to reveal the answer.
The answer is 543.
The answer is 11.
How did we get here?
The answer is 13.
How did we get here?
The answer is 543.
How did we get here?
The answer is 12.
How did we get here?
‘Difference’ refers to the subtraction of one number from another. It indicates the numerical distance between two values.
‘Sum’ refers to the result of adding two or more numbers together.
To find the sum of two numbers, add the two numbers together. The result will be the combined total of the two numbers.
Regrouping, also known as carrying, is a technique used in addition when the total in one place value (like the ones or the tens) is 10 or greater.
You simply take the 1 (like the 1 in 17) and add it to the next value place over to the left. This demonstrates that a number larger than 9 can be understood to be 10 + whatever is in the ones space.
To sum up, addition is a vital foundation for all maths skills to follow. With a little bit of practice, you’ll soon understand this cornerstone of maths and will be able to tackle more complex forms of arithmetic!

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
How to improve at mental maths
Learn some handy mental maths strategies that’ll make addition a breeze!
A guide to the KS1 maths curriculum
Discover all the topics children are introduce to in KS1 maths
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: