

Parallel lines are an important concept in geometry that we see everywhere we look in everyday life. In this guide, we’ll explore the definition of parallel lines and how we use them in maths!

Author
Christine
Published
October 10, 2023


In this guide, explore the definition of parallel lines and how we use them in maths!

Author
Christine
Published
October 10, 2023


Parallel lines are an important concept in geometry that we see everywhere we look in everyday life. In this guide, we’ll explore the definition of parallel lines and how we use them in maths!

Author
Christine
Published
October 10, 2023


Key takeaways
Table of contents
Parallel lines are a really important concept in maths that also have many real-world applications. They are lines that never intersect, no matter how far they are extended in either direction.
In this article, we’ll tell you everything you need to know about parallel lines, how to identify them and how they are used in the real world. Let’s get started!
Parallel lines are two or more lines that are always the same distance apart and never intersect, even if they’re extended infinitely in both directions.
They’re always equidistant (a fancy word for ‘at equal distances’) and run in the same direction, which means they have the same slope.
These lines are a fundamental in geometry and have many real-world applications. Don’t believe us? Parallel lines are used in architecture, engineering, navigation and even sports!

Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Parallel lines look like two straight lines that are always the same distance apart and never intersect, even if they are extended infinitely in both directions.
They can be represented by drawing two straight lines side by side with an arrowhead at each end to indicate that they continue infinitely in both directions.
Parallel lines always have the same slope, which means that if you were to draw a perpendicular line to one of the parallel lines, it would intersect the other line at a right angle.

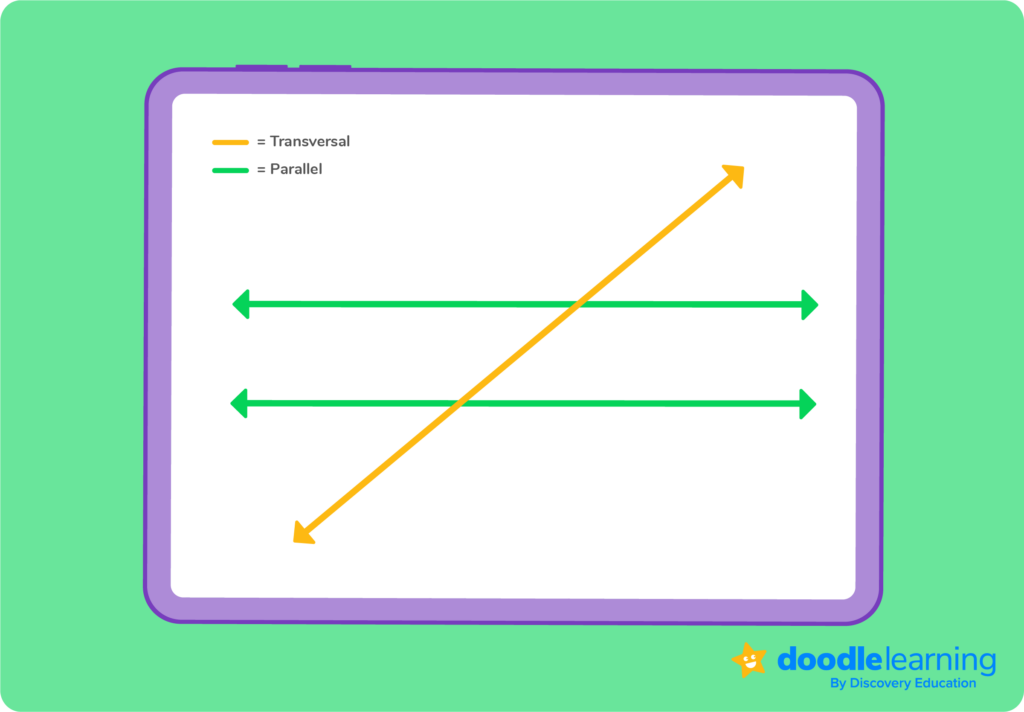
Now that you know what a parallel line is, it’s helpful to know what a transversal is.
This type of line intersects two or more other lines at different points. When a transversal intersects two parallel lines, it creates a set of angles like: corresponding angles, alternate interior angles and alternate exterior angles.
Understanding the properties of transversal lines and the angles they create is essential to solving many geometry problems and applying these concepts in practical, real-life situations.
Want to have a go at some questions? DoodleMaths is an app that’s filled with thousands of fun, personalised exercises exploring the whole primary curriculum!
Accessible on tablets, mobiles, laptops and desktops, DoodleMaths creates each child a unique learning experience programme tailored to their needs, boosting their confidence and ability in maths.
Created by teachers, it sets work at just the right level for each child and includes visual explanations for every topic, letting them work independently. Try it free today!

Parallel lines have several important properties that make them useful in geometry and real-world applications. Some of these properties include:
So what’s next? It’s easy to eyeball parallel lines, but you’ll want to know a way to prove it.
To determine that two lines are parallel, you need to demonstrate that they have the same slope and never intersect, no matter how far they are extended in both directions. There are a few proven ways to do this.
One way to prove that two lines are parallel is by using the slope-intercept formula, which is y = mx + b.
In this equation, m is the slope of the line and b is the y-intercept. If two lines have the same slope and different y-intercepts, then they are parallel.
Another way to prove that two lines are parallel is by using the transversal theorem, which states that if a transversal intersects two lines and the corresponding angles are congruent, then the lines are parallel.
Additionally, you can also use the alternate interior angles theorem, which states that if a transversal intersects two lines and the alternate interior angles are congruent, then the lines are parallel.
These methods are all essential in proving that two lines are parallel and are frequently used in geometry and many other fields.
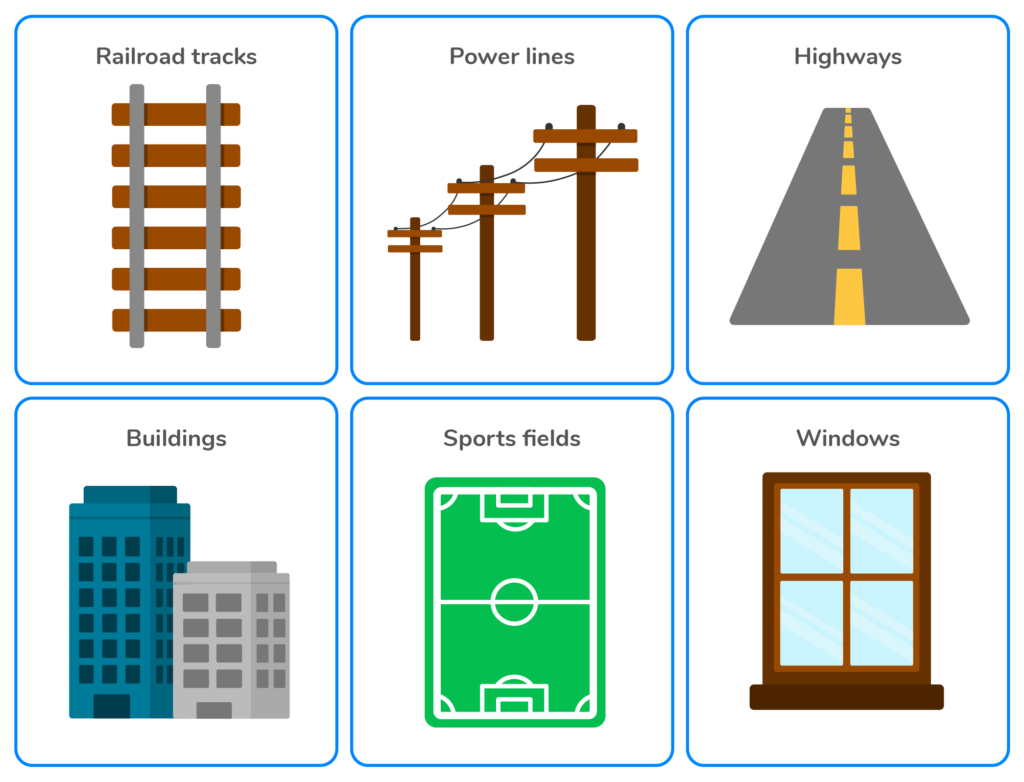
Look around and see if you can notice any parallel lines. They’re all around us, every day! Here are a few examples:
These are just a few examples of parallel lines in real life. Parallel lines have many more uses and can be found in many other objects and structures around us.
Now that you know all about parallel lines, what do you want to learn about next?
Maths doesn’t have to be complicated: it can be fun! DoodleMaths is an app that’s specifically designed to help kids build confidence and strengthen their skills across various topics. Interested? Create an account to start your free 7-day trial today!
There are three different types of parallel lines: horizontal, diagonal and vertical.
The opposite of parallel lines is intersecting lines.
Intersecting lines are two lines that meet or cross at a single point. Unlike parallel lines, intersecting lines have different slopes, and they intersect at a specific point.
Intersecting lines are also known as non-parallel lines, and they can form different angles depending on their intersection.
Different from parallel lines, intersecting lines are commonly found in nature and everyday objects, such as the intersection of roads, branches of trees, scissors and the edges of geometric shapes.
The symbol for parallel lines is two vertical lines that are placed side by side, just like this: ∥.
The symbol is used to indicate that two lines are parallel and will never meet or intersect, no matter how far they are extended in both directions.
If two lines have the same slope and different y-intercepts, then they are parallel.
The equation for this is y = mx + b.
For example, y = 2x + 1 and y = 2x + 5 represent two parallel lines.

The ultimate guide to 2D shapes
Explore the names and properties of some of the most common 2D shapes
What is a rhombus shape?
In this guide, discover the key properties of this unique four-sided shape!
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: