Discover the properties of this unique 4-sided shape!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Last updated: September 29th, 2023
Discover the key properties of this unique 4-sided shape!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Published: September 29th, 2023
In this guide, discover the key properties of this unique 4-sided shape!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Published: September 29th, 2023
Key takeaways
The word rhombus might sound a bit fancy, but it simply describes a four-sided shape, like a diamond, that shares many of the same properties as a square.
A diamond-shaped kite is a popular example of a rhombus if it has four equal sides. You may have also seen this shape in building designs and floor tiles.
So, what exactly is a rhombus? And how can we measure its perimeter or area? Let’s take a look!
The term ‘rhombus’ is derived from the Greek word ‘rhombos’, which means something that spins.
The definition of a rhombus is a four-sided shape, also known as a quadrilateral, with congruent sides. This means that all sides must be the same length.
All rhombuses are quadrilaterals, but not all quadrilaterals are rhombuses. A quadrilateral is a shape with four sides.
For example, a rectangle is a quadrilateral because it has four sides. However, in rectangles, two of the sides are shorter than the others, so while both a rectangle and a rhombus are quadrilaterals, a rectangle is not a rhombus.
Now, you might be thinking, ‘So, are a rhombus and a square the same?’.
Squares can be classified as rhombuses because they have four sides of equal length. However, a square must also have four equal angles of 90 degrees, which are known as right angles.
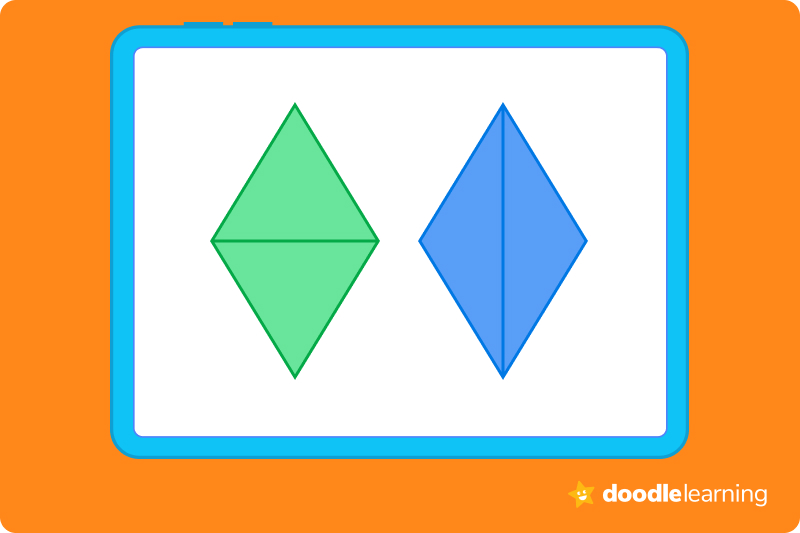
A rhombus only needs to have its opposite interior angles equal to each other, as illustrated below.
So, all squares are rhombuses, but not all rhombuses are squares!
A rhombus is a fairly rare shape in the natural world. However, it can be found in many man-made items. Have you ever played a game of cards? Rhombuses are used to symbolize the suit of diamonds. Some kites are in the rhombus shape too.
Rhombuses are also a popular choice for floor tiles, road signs, Christmas tree decorations, and building designs.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Get 2 FREE weeks of Doodle!
Use code 2WKS_AUTUMN to enjoy unlimited questions and games
Try DoodleMaths for free!
Select a year group
A rhombus is a quadrilateral with unique features that sets it apart from other quadrilaterals, such as a rectangle or a trapezoid.
For a shape to be classified as a rhombus it must:
The area of a rhombus is described as the amount of space inside the two-dimensional shape.
This is usually measured in units squared, for example, in centimeters squared (cm2) or meters squared (m2). Fortunately, because a rhombus has all sides of equal length, finding the area is more straightforward than with other shapes!
We can calculate the area of a rhombus shape in two ways:
Let’s go through the steps of each of these calculations.
8 x 6 = 48
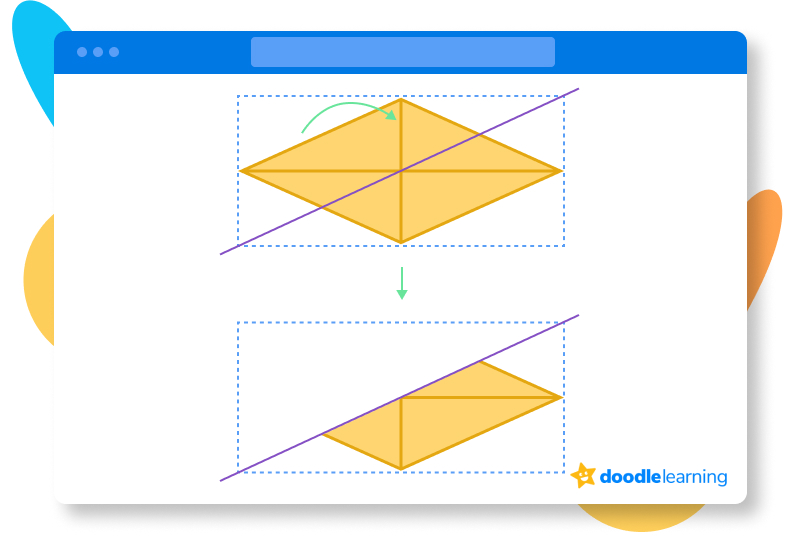
So, we divide the original answer by 2:
48 ÷ 2 = 24
The area of the rhombus is 24 cm2
5 x 7 = 35
So, in this example, the area of the rhombus is 35 cm2!
The perimeter of a rhombus is the total length of its boundaries. Basically, it’s the sum of all the side lengths. We know that all four sides of a rhombus are of equal length, which makes this a fairly straightforward calculation.
4 x 4 = 16
Want to have a go at some questions? DoodleMaths is an app that’s filled with thousands of fun, personalised exercises exploring the whole primary curriculum!
Accessible on tablets, mobiles, laptops and desktops, DoodleMaths creates each child a unique learning experience programme tailored to their needs, boosting their confidence and ability in maths.
Created by teachers, it sets work at just the right level for each child and includes visual explanations for every topic, letting them work independently. Try it free today!
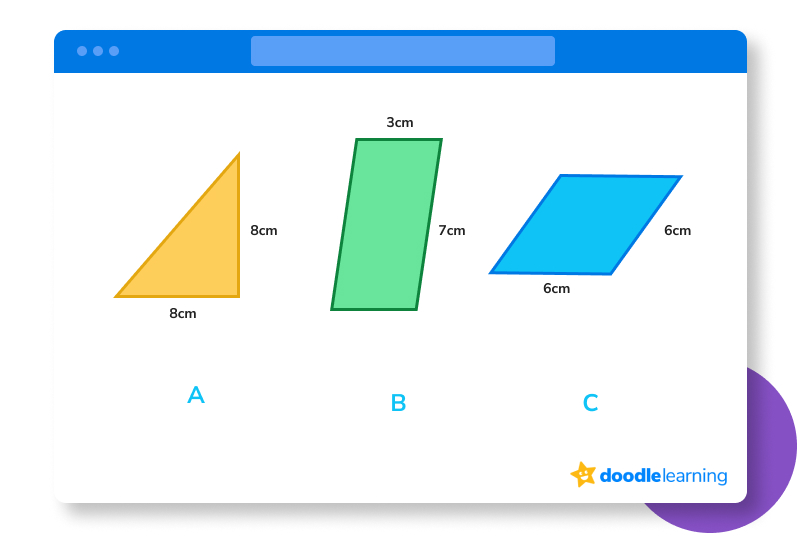
The correct answer is B because this is the only shape with 4 sides of equal length.
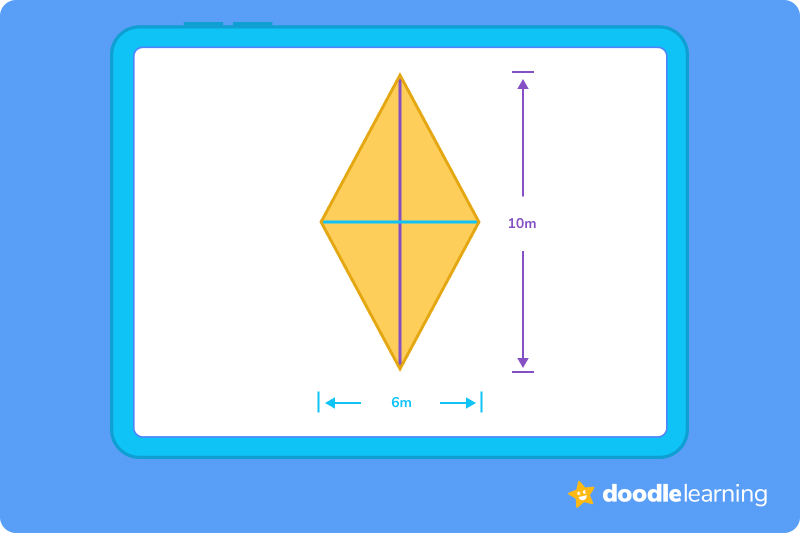
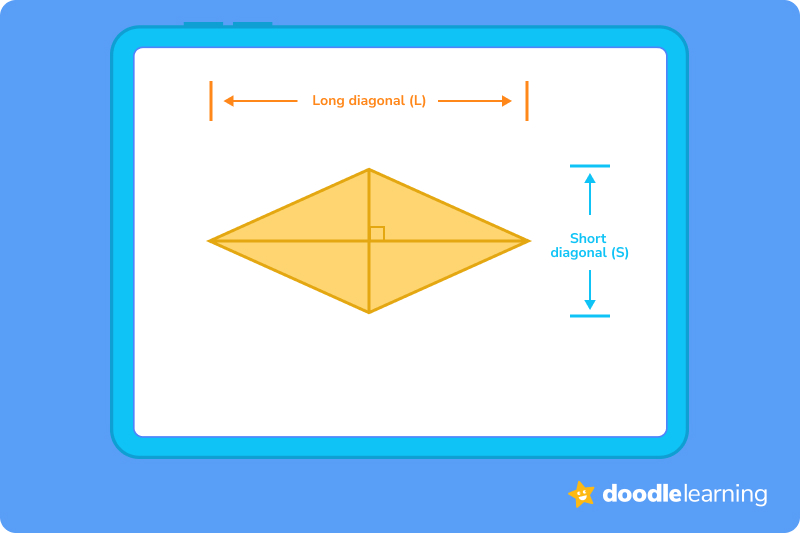
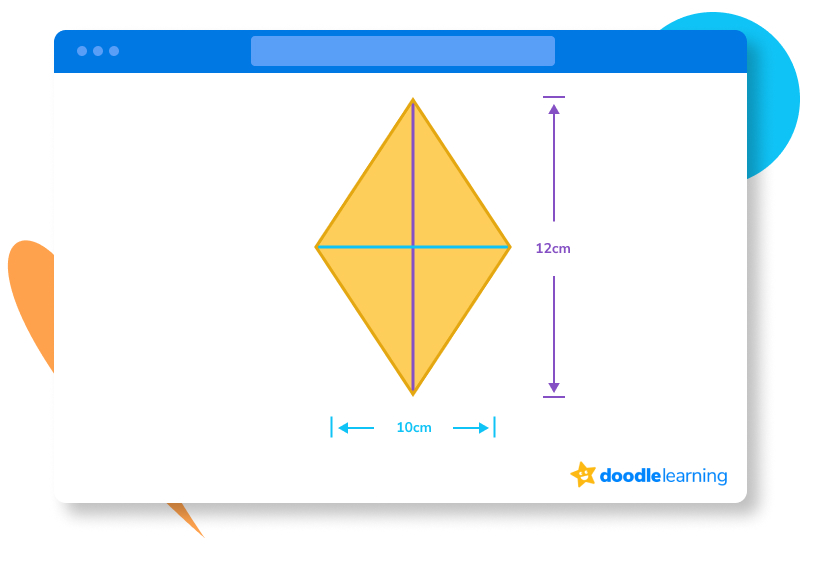
In this problem, we know the long and the short diagonal measurements of the rhombus. So, first, we need to multiply these two numbers together:
6 x 10 = 60
Now, because we are using diagonal measurements, we need to divide the answer by 2:
60 ÷ 2 = 30
Therefore, our answer is 30 m2.
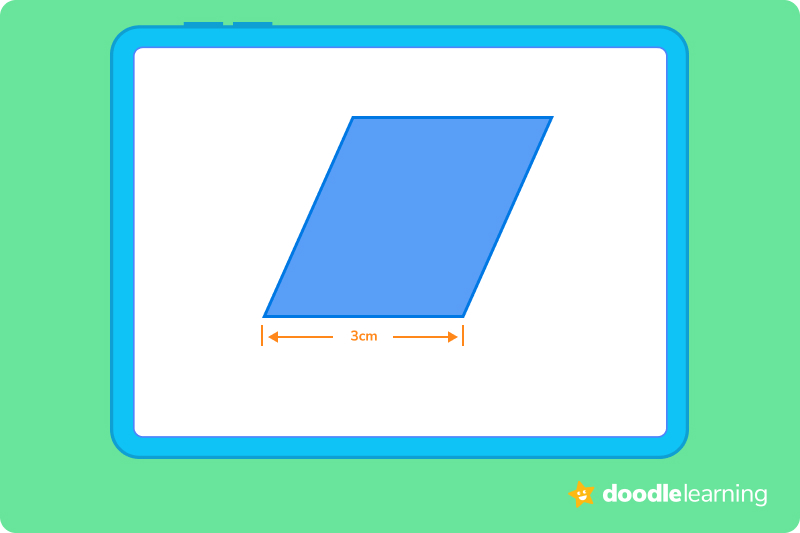
All four sides of a rhombus are the same length. So, if we know that one side is 3 cm, we just need to multiply this number by 4:
4 x 3 = 12
So, the correct answer is 12 cm.
Ready to give it a go?
Now it’s time to put your knowledge to the test! Work through the following problems on your own, and see how you do. Don’t feel disheartened if you struggle with any of the questions. Remember, practice makes perfect!
Feel free to look back through this guide to refresh your memory whenever you need to.
Click to reveal the answer.
The answer is 36 cm.
The answer is FALSE.
The answer is C.
The answer is 60 cm2.
The answer is 48 cm2
How did we get here?
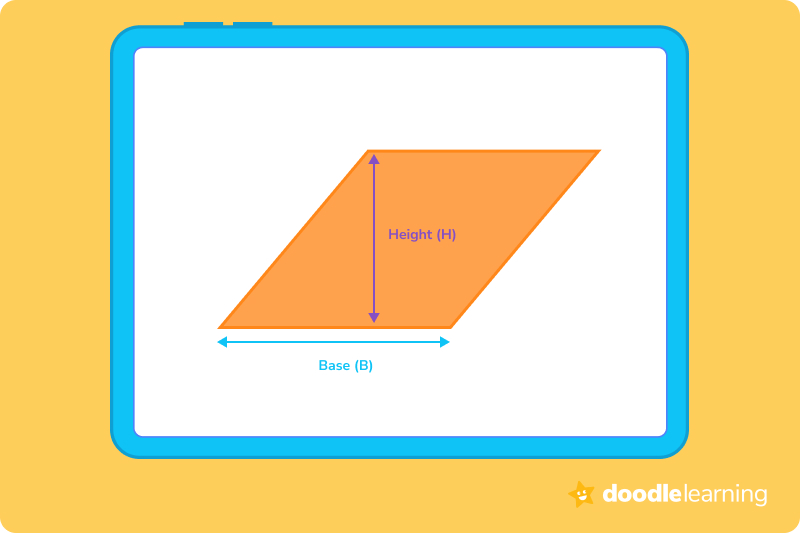
We have the base measurement and the height measurement of the rhombus in this example. So, all we need to do is multiply base times height:
8 x 6 = 48
This makes the answer 48 cm2
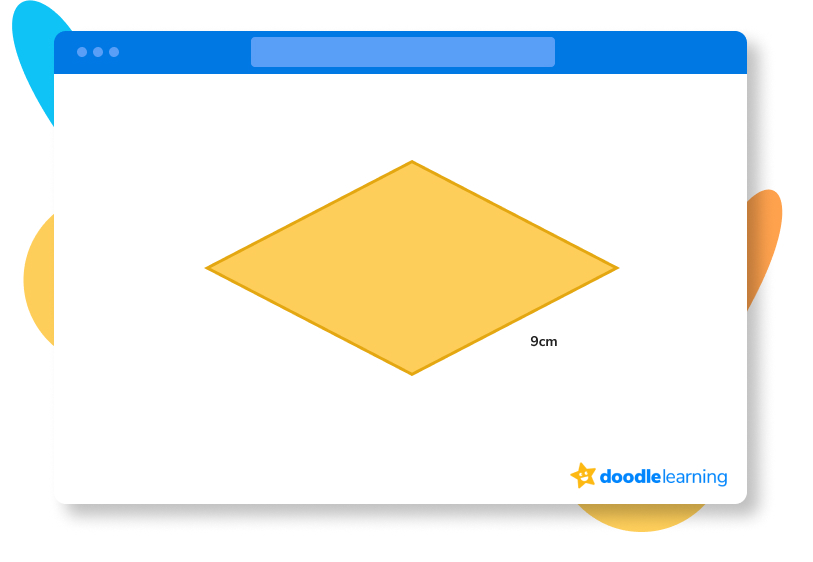
The answer is 36 cm
How did we get here?
A rhombus has 4 sides of equal length. So, if we know that one side is 9 cm, we just need to multiply this number by 4:
9 x 4 = 36
Therefore, the answer is 36 cm
The answer is FALSE
How did we get here?
In a rhombus, only the opposite angles must be the same. If a shape has four equal sides and 4 equal angles, then it’s a square.
The answer is C
How did we get here?
The answer is 60 cm2
How did we get here?
12 x 10 = 120
120 ÷ 2 = 60
Yes, a rhombus must have four sides of equal length. A rhombus must also have its opposite sides parallel and opposite angles equal.
For a shape to be a rhombus, it has to have four straight sides of equal length and the opposite angles need to be the same. The most common rhombus shape is a diamond. However, technically, a square can also be classified as a rhombus because it has four sides of equal length and the opposite angles are equal. However, it is important to note that not all rhombuses are squares because rhombuses don’t all have 90° angles.
If a rhombus is a square then it must have 4 right angles. However, for a shape to be classified as a rhombus, it only needs to have the opposite angles equal, and it is not required that they are right angles.
There are certain properties that a shape must have to be a rhombus:
Lesson credits
Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching maths. She's currently working as a Business Analyst and is earning a masters degree in Business Administration.
Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics. She's currently working as a Business Analyst and is earning a masters degree in Business Administration.
The ultimate guide to 2D shapes
Explore the names and properties of some of the most common 2D shapes
3D shapes: names and properties
From spheres to cubes, we explore everything you need to know
Roman numerals from 1 to 100
Learn the Roman numerals from 1 to 100 and have a go at some questions!
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
