

Learn how to convert decimals to fractions with our step-by-step guide

Author
Amber Watkins
Published
November 7, 2023


Learn how to convert decimals to fractions with our step-by-step guide

Author
Amber Watkins
Published
Nov 7, 2023


Learn how to convert decimals to fractions with our step-by-step guide

Author
Amber Watkins
Published
Nov 7, 2023


Key takeaways
Table of contents
Converting decimals to fractions doesn’t have to be intimidating. If you can read a decimal, you can change that decimal into a fraction!
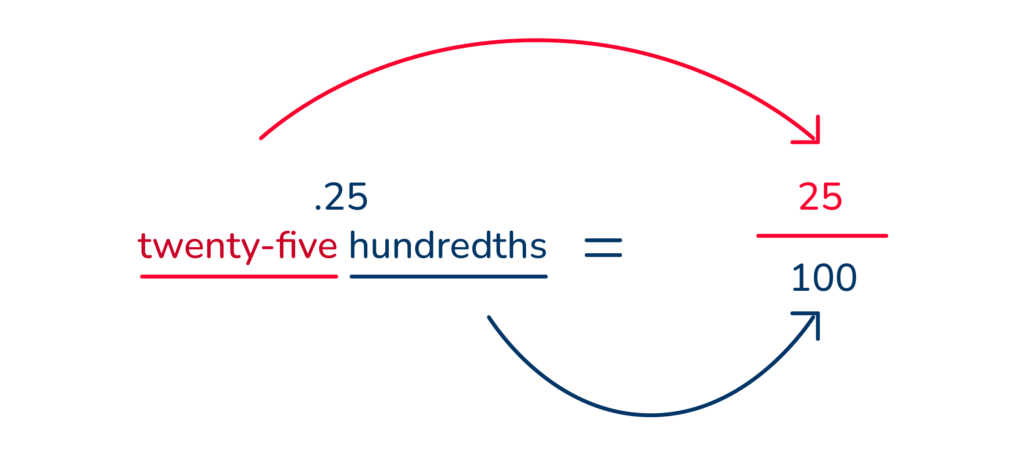
When you read .25 you say ‘twenty-five hundredths’. The number 25 is placed on the top of the fraction and 100 on the bottom.
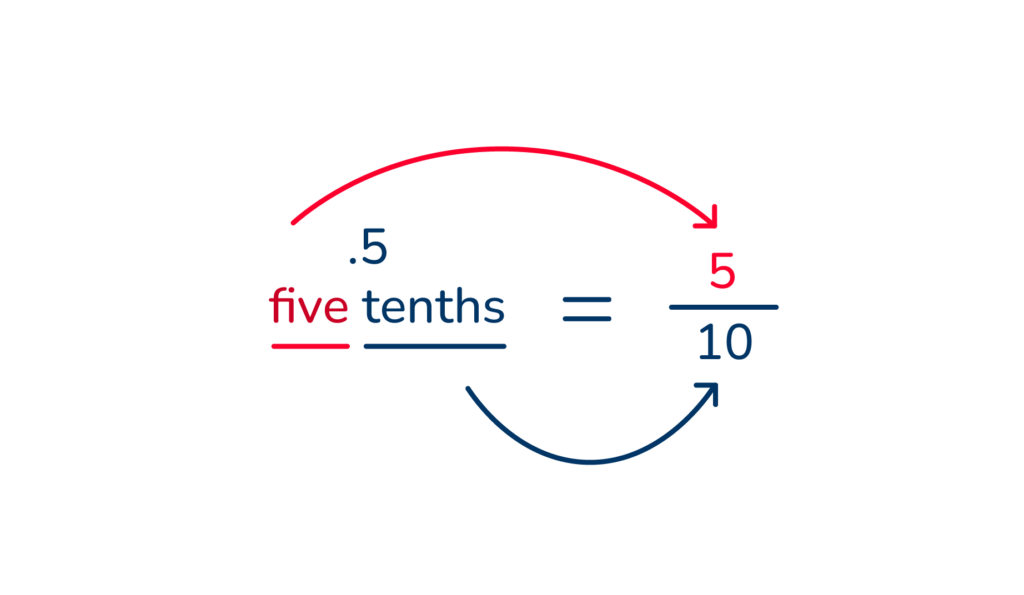
When you read .5 you say, “five tenths”. The 5 is placed on the top of the fraction and 10 on the bottom.”
When converting decimals to fractions, how do we know to say hundredths? Tenths? or thousandths? This is where understanding place value comes in.
Let’s briefly go over the most common place values found in decimals. Then we can review how to convert decimals to fractions using place values.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
The most common decimals have up to three place values: tenths, hundredths, and thousandths place.
The place value of the last digit will be the number used as the denominator, or bottom number, of the fraction.
Denominator rules:
Then how do we get the numerator or the number on top of the fraction? Use the number words prior to the place value words. Let’s practice this together a few times:
What numbers would you use as the numerators and denominators when converting each decimal to a fraction?
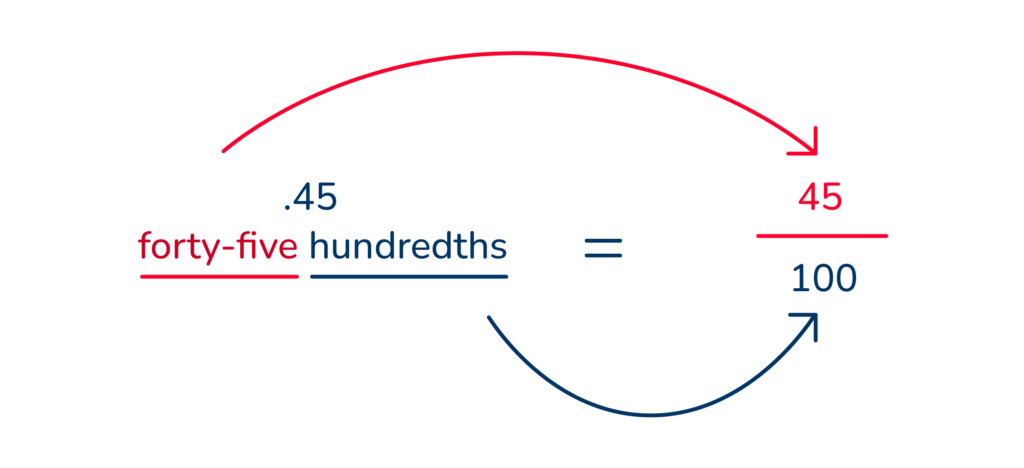
.45 ‘forty-five hundreths’
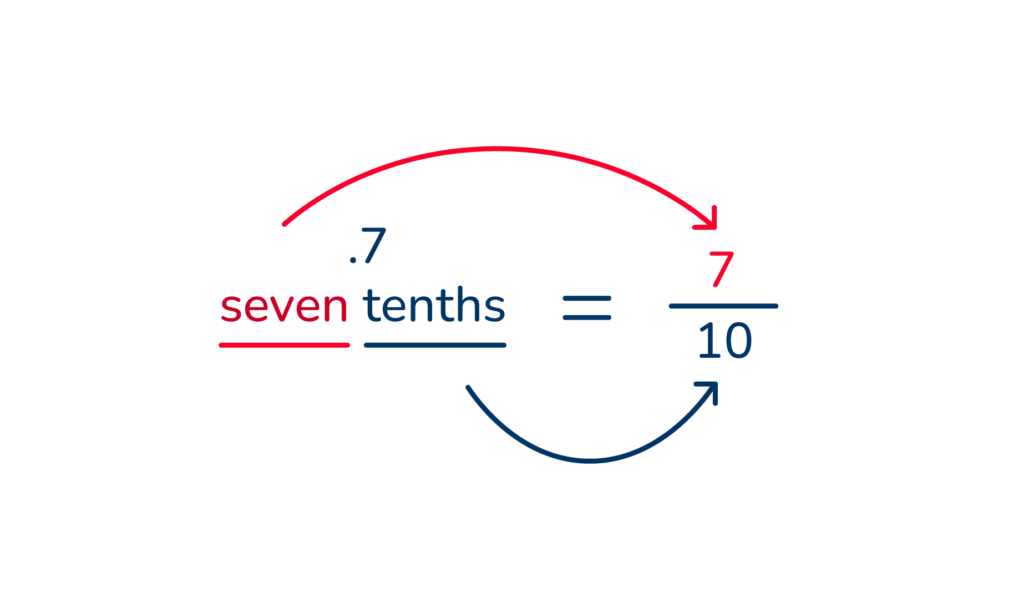
.7 ‘seven tenths’
.865 ‘eight hundred and sixty-five thousandths’

Let’s put these steps together to see how to convert decimal to fraction equivalents.
Ask yourself when reading this decimal, did I use the word tenth, hundredth, or thousandth?

Reducing a fraction means changing a fraction to its simplest form. We reduce a fraction by:
1. Finding the (Greatest Common Factor) GCF of the numerator and the denominator
2. Then we divide the numerator and denominator by that number
For example: How do we reduce the fraction 2/4? The GCF of 2 and 4 is 2. So we would divide the top and bottom numbers by 2 and get ½.
Let’s see how this is done with the decimal .95.
1. When reading the decimal .95 we would say, “ninety-five hundredth”. The reason we chose the word hundredth, is because the last digit “5” is in the hundredths place.
2. Because the last digit 5 is in the hundredths place, 100 will be our denominator.
3. Our numerator, or top number, will be the number word: ninety-five.
4. Now we reduce. The GCF of 95 and 100 is five. So, we divide the top and bottom numbers by 5 to get 19/20 as our final fraction.
The more you convert decimals to fractions, the more you will remember what decimals are as fractions. Would you like a sneak peek of the most common decimal-to-fraction conversions?
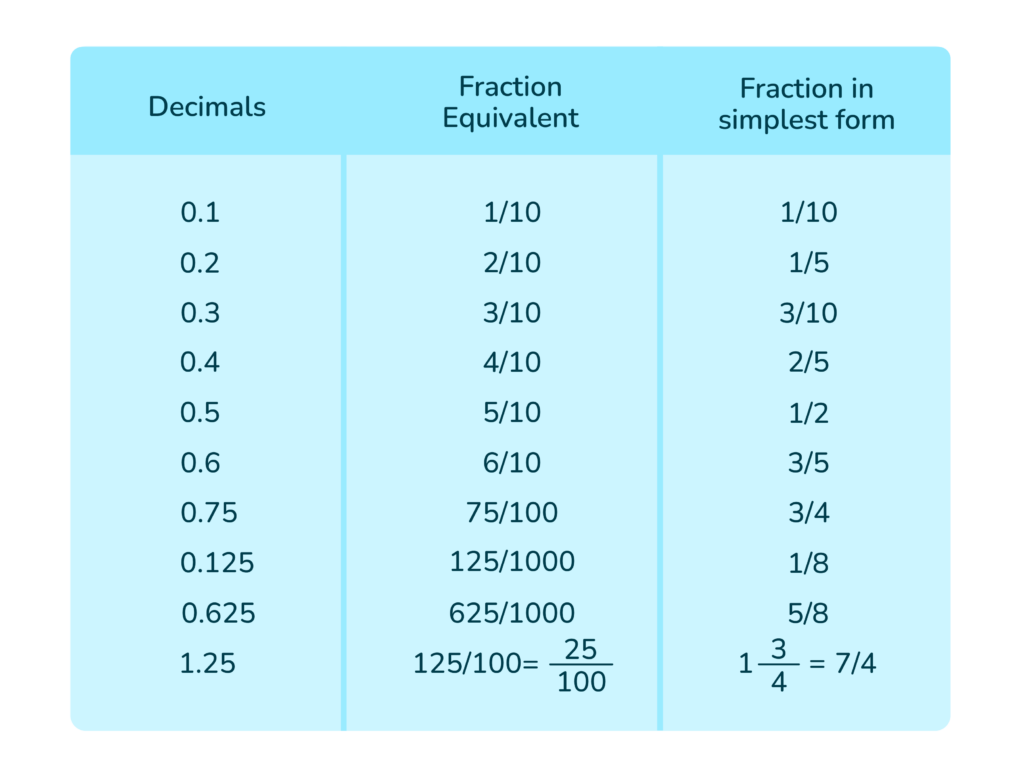
Converting repeating decimals to fractions
What do you do when you are given a repeating decimal? Can the same steps apply? Yes! But we must remember that any fraction you create using these steps will only be an estimate. Let’s see how this can be done.
Convert the repeating decimal of .333333… to a fraction.
First, you must choose an ending point for your decimal. Let’s choose two decimal places .33. Then, you can follow the same 4 steps.
1. When we read the decimal .33 we read “thirty-three hundredths” because the last three is in the hundredths place.
2. Since the last decimal is in the hundredths place, the denominator will be 100.
3. The number word before the word hundredth is “thirty-three” so that will be our numerator.
4. Our final fraction will be 33/100. It can not be reduced.
We have to remember, when converting repeating decimals to fractions in this way, our fractions will be an estimate. The fraction 33/100 is exactly equal to .33 not .3333333 repeating. But it gets us close enough to use as a fraction.
There is a way to get a perfectly equivalent fraction. However, it may take a bit more practice to master.
What if we wanted to convert a decimal with a whole number such as 3.65? Do we follow the same step-by-step approach for converting decimals to fractions? Yes. With one added feature. Instead of making a proper fraction, we will make a mixed number. Let’s see how!
1. When we read the decimal 3.65 we say “Three and sixty-five hundredths.” Because the last digit 5 is in the hundredths place.
2. Since the last digit is in the hundredths place, we use 100 as the denominator.
3. The number word “sixty-five” will be used as the numerator of the decimal. Notice we didn’t include the whole number 3 as part of the fraction. Why not? Because 3 is a whole number and will be represented as a whole number.
4. Use 3 as a whole number before 65/100 to get 3 65/100.
Click on the boxes below to see the answers!
First, read the decimal. Whichever place value the last digit is will be the denominator (10, 100 or 1000). Place the number word as the numerator. Finally, reduce the fraction with the GCF if necessary.
You convert a fraction into a decimal by dividing the numerator by the denominator.

How to multiply decimals
Master multiplying decimals with our step-by-step guide and practice questions
Lesson credits

Amber Watkins
Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"

Amber Watkins
Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: