You may have heard of irrational numbers, but what exactly are they? In this guide, we take a look at a simple definition and some examples!
Author
Team Doodle
Published
Sep 20th, 2023
You may have heard of irrational numbers, but what exactly are they? In this guide, we take a look at a simple definition and some real-life examples!
Author
Team Doodle
Published
Sep 20th, 2023
We take a look at a simple irrational number definition and some real-life examples!
Author
Team Doodle
Published
Sep 20, 2023
Key takeaways
The irrational number is said to have been discovered by the Greek philosopher Hippasus around the 5th century BC.
At the time, his discovery wasn’t met with approval because most Pythagoreans believed that only positive, rational numbers could exist. The legend goes that he was made fun of for his discovery – and that he was even thrown into the sea!
Thousands of years later, we now know numbers can be categorised as both rational and irrational. But what does this mean exactly?
While it may seem complicated, once you understand what an irrational number is, there’s a very simple way to recognise them. Let’s find out more!
Put simply, an irrational number is any real number (a positive or negative number, or 0) that can’t be written as a fraction.
The fancier definition states that an irrational number can’t be expressed as a ratio of two integers – where p/q and q≠0. If a number can’t be written this way, it’s not a rational number.
One clue that a number is irrational is if it never ends or never repeats when written as a decimal. Here are some more ways to identify irrational numbers:
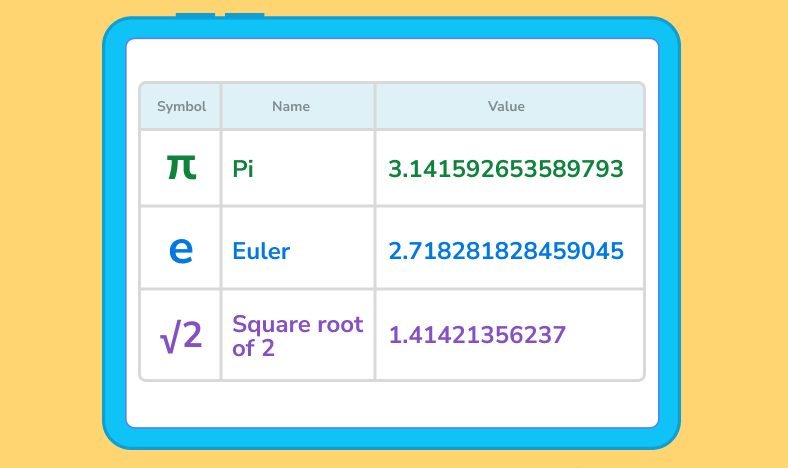
What are some ways you might see an irrational number? Some of the most famous irrational numbers are Pi, Euler’s Number and the Golden Ratio.
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
Get 2 FREE weeks of Doodle!
Use code 2WKS_AUTUMN to enjoy unlimited questions and games
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!
Since all irrational numbers are also real numbers, they obey the same set of properties as all real numbers.
Here are some ways irrational numbers interact in the maths world:
Irrational numbers and rational numbers are both valid numbers, even though they are displayed in different ways. In fact, they have more in common than you think!
Did you know that you can often multiply two irrational numbers (factors) to get a rational number (product)? Just because an irrational number may seem difficult to write or display, it can be very useful in maths – just like a rational number.
The main difference between rational numbers and irrational numbers is that rational numbers can be written as fractions and irrational numbers can’t.
Try DoodleMaths for free!
Select a year group
Irrational numbers are numbers that can’t be written as a fraction.
You can identify an irrational number by first turning it into a fraction. If it can’t be done, it’s likely irrational. Another clue is that many irrational numbers can be displayed as decimals that go on without an end or pattern. An example of this is Pi.
Irrational numbers are, in fact, real numbers. You can multiply them and add them to other numbers, just like rational numbers!
While they aren’t always easy to work with, irrational numbers have an important place in maths and our world.
Rational and irrational numbers are both real numbers.
Both types of numbers can be added, multiplied, and treated like any other number; you’ll just not be able to cleanly display irrational numbers as a simple ratio as you can with rational numbers.
Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!
Rational vs irrational numbers
Learn about the differences between rational and irrational numbers
Roman numerals from 1 to 100
Learn the Roman numerals from 1 to 100 and have a go at some questions!
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
