
Author
Christina Levandowski

Expert Reviewer
Jill Padfield
Published: January 2024


Get it right with your right angles in this easy measurement guide!

Author
Christina Levandowski

Expert Reviewer
Jill Padfield
Published: January 2024




Get it right with your right angles in this easy measurement guide!

Author
Christina Levandowski

Expert Reviewer
Jill Padfield
Published: January 2024


Key takeaways
Learning how to measure angles is one of the most important skills you’ll learn to prepare you for geometry and higher-level math classes. It’s simple to do once you’ve got the right tools and know-how — and we’re here to walk you through it!
Here’s our helpful step-by-step guide to measuring angles.
Here are some basic terms to keep in mind as you practise measuring angles.
Students generally will be familiar with the measurable unit of a degree — especially if they’ve had experience setting the temperature on an oven or determining how cold it is outside.
However, that’s not the type of degree we’re referencing when we say “degree” or “degree angle” when measuring angles. Instead, we’re applying a secondary, separate meaning and using it as a unit of measurement for angles that are measured by a protractor.
You’ll still use the degree symbol (°), or you can simply write “degrees” after your answer to clarify and finish it.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Radians aren’t something most KS2 students are familiar with yet. However, they will run into it later on — so we wanted to mention it here.
Radians are another unit of measurement that can be used in place of degrees when we measure angles. You’ll use these more in higher-level maths classes and applied maths classes (like physics) — so simply knowing the difference between the two is good enough for now.
You know that degrees and radians are different forms of measurement…but you’re likely wondering: How are they so different?
While both can be used to measure angles, degrees are slightly more “basic” than radians — they can be measured using a protractor (just like we’d see a centimeter mark on a ruler do).
Radians are a little more complex of a unit and can do more in higher-level maths. The formal definition states that they represent a ratio, otherwise known as the relationship between two different quantities.
This ratio is then divided by the length of the radius of a shape, which is normally a circle or a circular shape.
⚠️ There are 2π radians in any circle. You might notice how this corresponds with the formula for the circumference of a circle: C (circumference) = 2πr — where “r” = radius and π is and will always be 3.14.
🎉 Don’t worry about mastering that now, though — you’ll revisit radians later on. For now, let’s focus on learning how to measure using the designation of degrees.
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!


The first step to a correct calculation is getting accurate measurements on those angles.
Here’s our helpful how-to for kids, covering instructions for protractor measurement.
There are many different types of angles you’ll see as you practise measuring angles. Here are a few key types to remember as you practise your measurement:
Acute angles are angles where the measure of the angle is greater than 0° but less than 90°. These angles will look narrow, like fingers pinching something small. An easy way to remember these is to think that they are small, tiny, and, generally, look “cute.”

An obtuse angle is larger, measuring between 90° and 180°. Think of obtuse angles as large, or looking like “wide-open” mouths ready to chomp on your pencil.

Right angles are mathematically defined as angles that are exactly 90° — no more and no less. You can identify them by their clean, sharp appearance, with the two lines or rays creating a “box like” angle at the vertex, where they meet.

Straight angles are simple — they are defined as angles that are exactly 180°, which means that they’ll look like a straight line on your paper.

Angles aren’t just something you’ll see on worksheets or homework packets. They’re actually all around us in our daily lives! Our suggestion is to take an “angle hunt” around your house to see how many you can find. Doing this will help you to easily identify angle types, which is a great starting point for other types of angle measurement later on. You won’t even need an actual protractor to spot them!
Not sure where to start? Here are a few places that likely have angles around your home:
Go take a quick walk, and see what you can find. Don’t forget to tell yourself “good work” after!
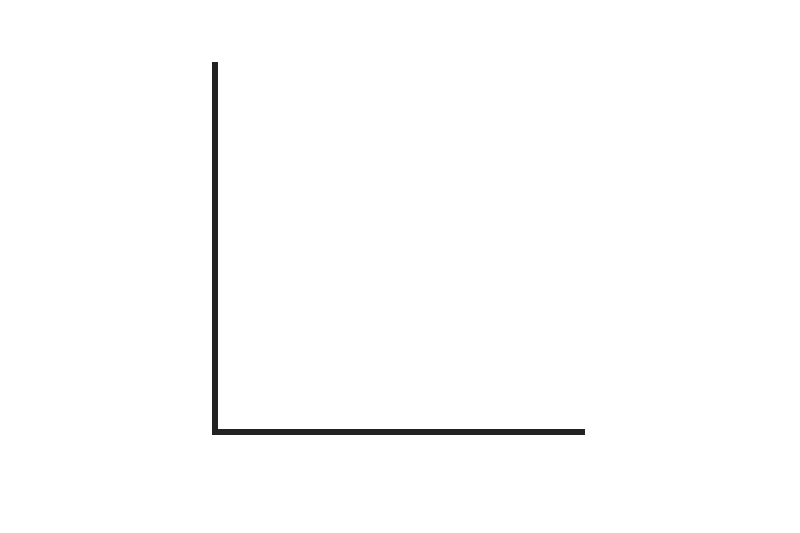
1. Measure the given angle:
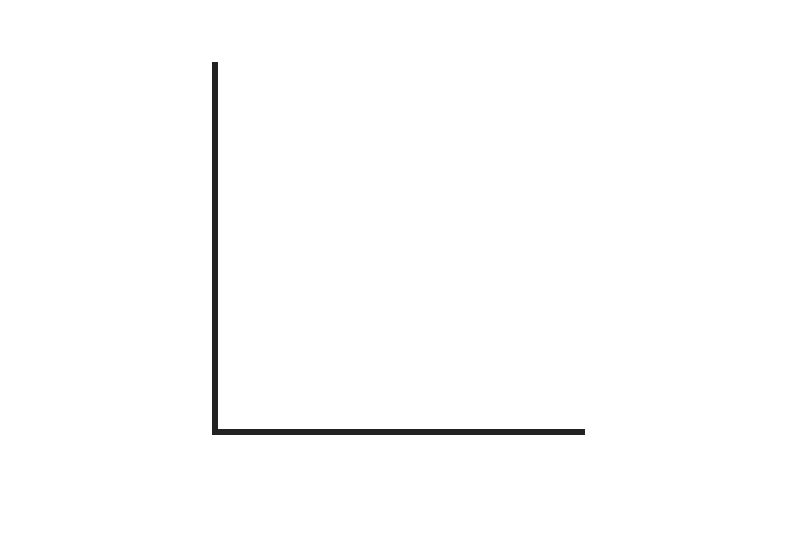
2. Measure the given angle:

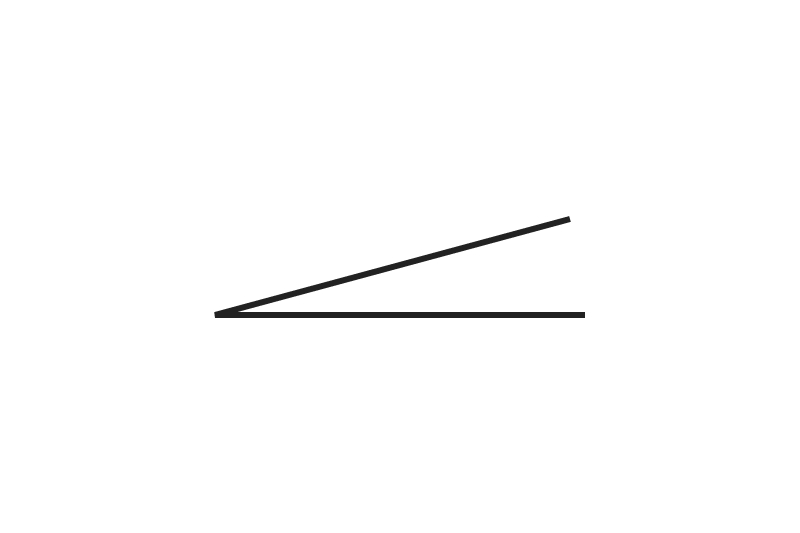
3. Measure the given angle:
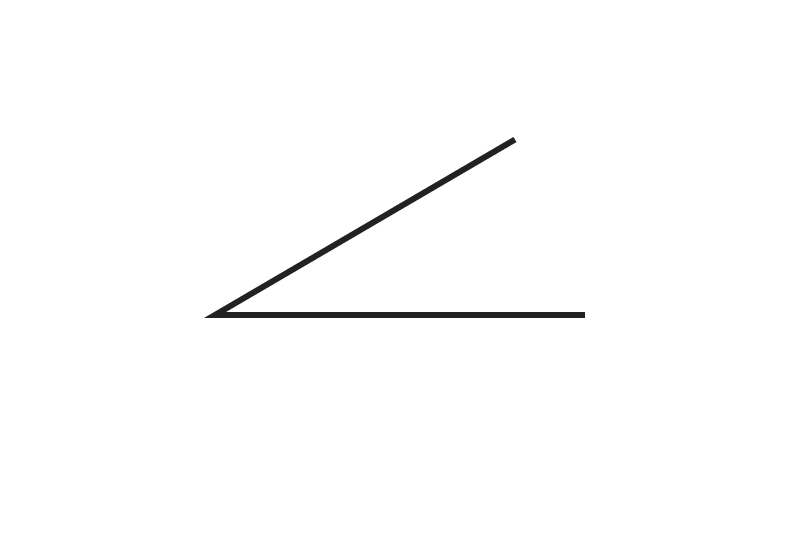
Ready to give it a go?
Now, it’s your turn! We’re confident that you now know the basics to angles and angle measurement. Now, it’s time to practise.
Don’t be afraid to try and fail. It’s all part of the process! Remember that practise makes perfect, and know that you’re just a few sessions away from acing that next maths exam. You’ve got this!
Click to reveal the answer.
The answer is 180 degrees.

The answer is 90 degrees.
The answer is 15 degrees.
The answer is 150 degrees.
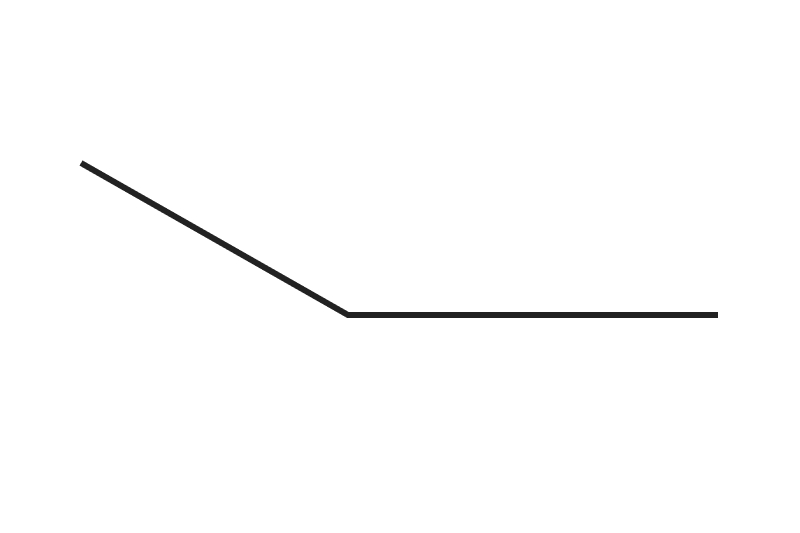
The answer is 70 degrees.
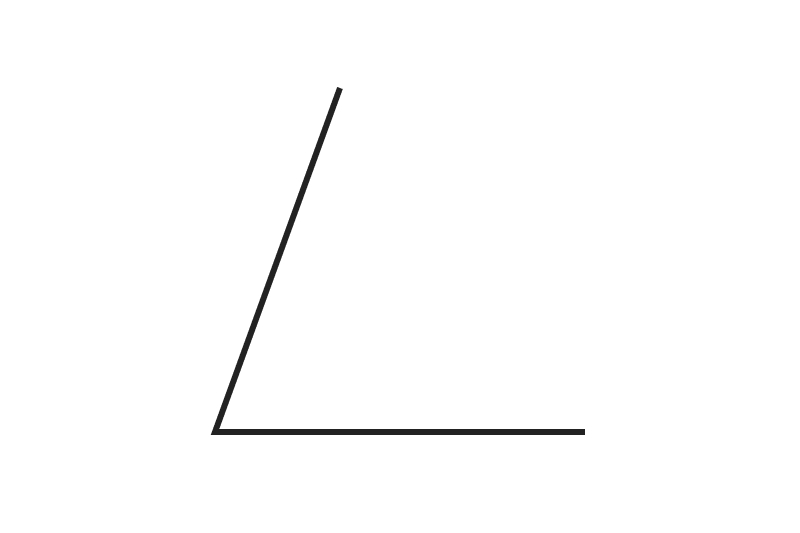
The answer is 180 degrees.
How did we get here?
The answer is 90 degrees.
How did we get here?
The answer is 15 degrees.
How did we get here?
The answer is 150 degrees.
How did we get here?
The answer is 70 degrees.
How did we get here?
Sign up for the DoodleMaths app today!
Turn maths into an adventure when you sign up for DoodleMaths.
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
Use your protractor and place the midpoint at the vertex of your angle. Align the base line or ray with the “0” mark, and determine what class of angle it is (i.e., acute, obtuse, right, straight). Then, follow the second line of the angle and record where it is pointing to on the protractor.
Many find that the easiest way to measure angles is to use a protractor.
A right angle is an angle that is exactly 90 degrees.
A straight angle appears as a flat line and is an angle that is no more or no less than 180 degrees.


Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Lesson credits

Christina Levandowski
Christina has written for hundreds of clients from small businesses to Indeed.com. She has extensive experience working with marketing strategy and social media marketing, and has her own business creating assets for clients in the space. She enjoys being an entrepreneur and has also started pursuing investment opportunities as time permits.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Christina Levandowski
Christina has written for hundreds of clients from small businesses to Indeed.com. She has extensive experience working with marketing strategy and social media marketing, and has her own business creating assets for clients in the space. She enjoys being an entrepreneur and has also started pursuing investment opportunities as time permits.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: