The identity property explains how numbers can stay the same—even when they’re multiplied.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: February 2024


The identity property explains how numbers can stay the same—even when they’re multiplied.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: February 2024




The identity property explains how numbers can stay the same—even when they’re multiplied.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: February 2024


Key takeaways
Identities work just the same way for numbers as they do for you, me, and practically everything else in the world. Just like how your friends, teachers, and relatives all have their own specific identities, so do numbers! And that doesn’t always have to change, even when you’re doing maths.
The identity property of multiplication explains how every number can be multiplied by something, and still keep the same identity it had when you started. Follow along as we teach you exactly how that works.
The identity property is one of four main rules applied to multiplication—the others including the distributive, commutative, associative, and zero properties.
If you want to learn how multiplication works, understanding the identity property is a good first step. The identity property is the simplest of the five, so let’s make sure we get it down pat before we move on to the more complicated ones.
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
The identity property of multiplication states that any value multiplied by 1 will equal that same value. This fact follows the reasoning behind repeated addition and how multiplication serves as a quicker form of this addition.
To multiply something means to add a certain value a repeated amount of times.
For example:

The four in the equation above represents the amount of times six is added to itself. This means that in a multiplication equation where a value is only multiplied by one, there is only one of that value. It won’t be added to itself at all; it’ll be exactly the same as it was before the multiplication. Think about the following problem:
Janice got 12 chocolate bars for Halloween. All 12 of those chocolates came in one bag. Write an equation that shows this.
For this problem, we could express the amount of chocolate bars with the following equation: 12 1, since we know there’s 12 bars in just one bag. There aren’t any other bags with bars we can add to the 12 we already have, so we can just write our expression with a one. This lets us know that there are only 12 bars in total.
The identity property of multiplication reflects this rule. Any number multiplied by one will stay exactly the same, as if it weren’t multiplied by anything at all!
This applies the same way to decimals, fractions, and whole numbers alike. Anything multiplied by one will stay exactly the same. Not so bad, right? Keep following along as we discuss how the identity property works with different kinds of numbers.
You might also see the identity property of multiplication referred to as the multiplicative identity property of 1, or just the identity property.
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!


Even though we might already understand how the identity property works based on what we’ve already talked about, let’s go ahead and define a specific formula for it just to be sure.

In this formula, (a) represents any real number.
The identity property works the same way with integers as it does with any other number. Just remember that whenever you multiply an integer by 1, the product will be the same value as the original integer. It will never change! This even applies to negative numbers, like in the following equation:
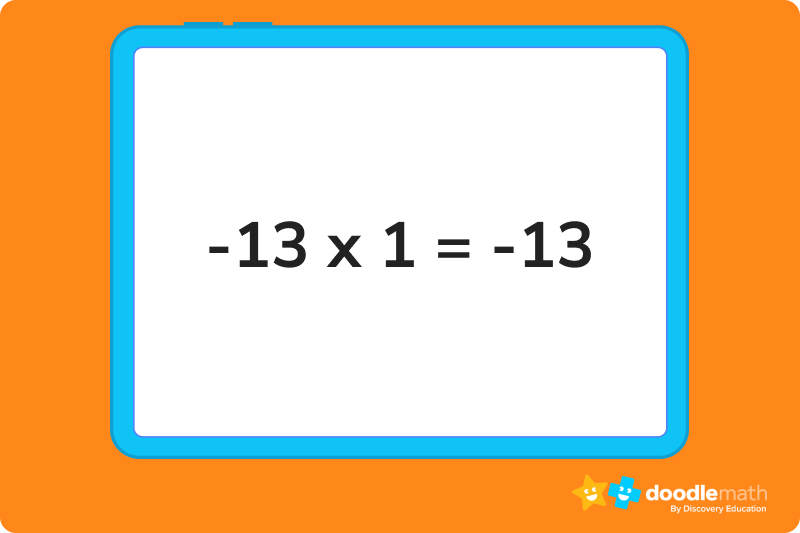
The rules don’t change just because the integer happens to be negative. If you’re multiplying by 1, the integer stays the same.
All rational numbers operate exactly the same way when multiplied by 1. As we’ve mentioned before, any number—be it rational or whole—will always be equal to itself when multiplied by 1. The identity property works the same way across all kinds of numbers!
There are other properties of multiplication besides the identity property that further define how multiplication works. There are four other rules in total, known as the commutative property, the associative property, the distributive property, and the property of zero.
These properties are equally important to understand as basic guidelines for multiplication. Let’s take a look at each rule and see what they say about how we multiply things.
The commutative property of multiplication talks about the placement of numbers in a multiplication equation, and how this placement can affect the product. Basically, the commutative property states that the order of numbers can be switched within an equation without changing the outcome of the multiplication. For example:

In the equation above, even if the 3 and 9 are switched in their positions, the outcome of the multiplication is the same. Swapping the positions of numbers does not affect the product.
The associative property states that when you multiply different numbers together, the grouping of these numbers has no effect on the product. You can group numbers together in different ways within a multiplication problem without producing a different value. Look below:

Here, the grouping of 13 and 7 on the left side is different from the grouping of 7 and 13 on the right. The associative property tells us that this doesn’t matter, as the product of the multiplication is the same regardless of how you choose to group your numbers.
The distributive property discusses what you can do when solving a problem where one number is multiplied by the sum or difference of two other numbers. These equations will look like the following:

Normally we would solve this problem by using the order of operations and solving the subtraction problem already within the parentheses. However, the distributive property states that we can distribute (multiply) the 17 by 4 and subtract this from the product of 17 and 13. It should look like the following:

Instead of using the order of operations, the distributive property lets us multiply 17 by both numbers inside the parentheses, and then find the difference of those two products. The end value will be the same as if we had used order of operations instead.
The property of zero is about as simple as the identity property. The zero property states that any number (rational, whole or any kind of integer) multiplied by zero will equal zero. For example:

Sign up for the DoodleMaths app today!
Turn maths into an adventure when you sign up for DoodleMaths.
Yes. The identity property applies the same way to negative numbers as it does to all others. The fact that a number is negative doesn’t change how it works under the identity property. Multiplying by one will still give you the same negative value.
The identity property gets its name from the fact that the identity of the number itself doesn’t change after being multiplied. Multiplying by one has no effect on the value of the number being multiplied. This gives us a convenient way of remembering the rule of the property. The identity never changes!
Yes, there is! And the identity property of division works the exact same way as the identity property of multiplication. Any number divided by one will provide you with the same value as the original number itself. Just like when dealing with multiplication, the identity property of division applies to all real numbers, rational numbers, whole numbers, and integers alike.
No, the identity property does not work the same way when the one is negative. Multiplying a number by a negative one will change the sign of the original value, meaning it doesn’t follow the rules of the identity property.


Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: