

Does the order in which we solve maths problems matter? Yes! Let’s learn about the order of operations in maths, aka BODMAS, to solve multi-step expressions.

Author
Amber Watkins
Published
July 2024


Does the order in which we solve maths problems matter? Yes! Let’s learn about the order of operations in maths, aka BODMAS, to solve multi-step expressions.

Author
Amber Watkins
Published
July 2024


Does the order in which we solve maths problems matter? Yes! Let’s learn about the order of operations in maths, aka BODMAS, to solve multi-step expressions.

Author
Amber Watkins
Published
July 2024


Key takeaways
Table of contents
When reading a maths problem, we usually start from left to right. So it is natural to want to solve problems in the same way. Does this method get us the right answer for every problem?
Let’s solve the following problem in two ways to see how order makes a difference: 3 – 2 x 5 =
1. You can solve this problem by subtracting first.
3 – 2 x 5
1 x 5
5
2. Or you can solve it by multiplying first.
3 – 2 x 5
3 – 10
-7
In both examples, we took the same actions: we multiplied and subtracted, but switched the order. As a result, we found two very different answers. How can we know which is the right answer? By following the maths order of operations.
What is the order of operations? The order of operations tells us the order in which to perform operations when the problem contains more than one kind of operation.
Operations are the actions we take in maths. The most common maths operations are adding, subtracting, multiplying, dividing, simplifying exponents, and finding square roots.
Some maths questions have more than one kind of operation in the problem. How can we solve those types of expressions? We follow the order of operations!
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
Get 1 FREE month of Doodle!
Use code MONTH_2026 to enjoy unlimited questions and games
Want to learn more about the order of operations? DoodleMaths is an award-wining maths app that’s proven to double a child’s rate of progression with just 10 minutes of use a day!
Filled with fun, interactive questions covering the whole curriculum, it creates each child a unique work programme tailored to their needs, boosting their confidence and skills in maths. Try it free today!


Many times you will see the order of operations called BODMAS. What is BODMAS? BODMAS is an acronym that helps us remember the order in which to solve multi-operational problems.
What does BODMAS stand for? BODMAS is an acronym that stands for Brackets, Orders, Division or Multiplication, Addition or Subtraction.
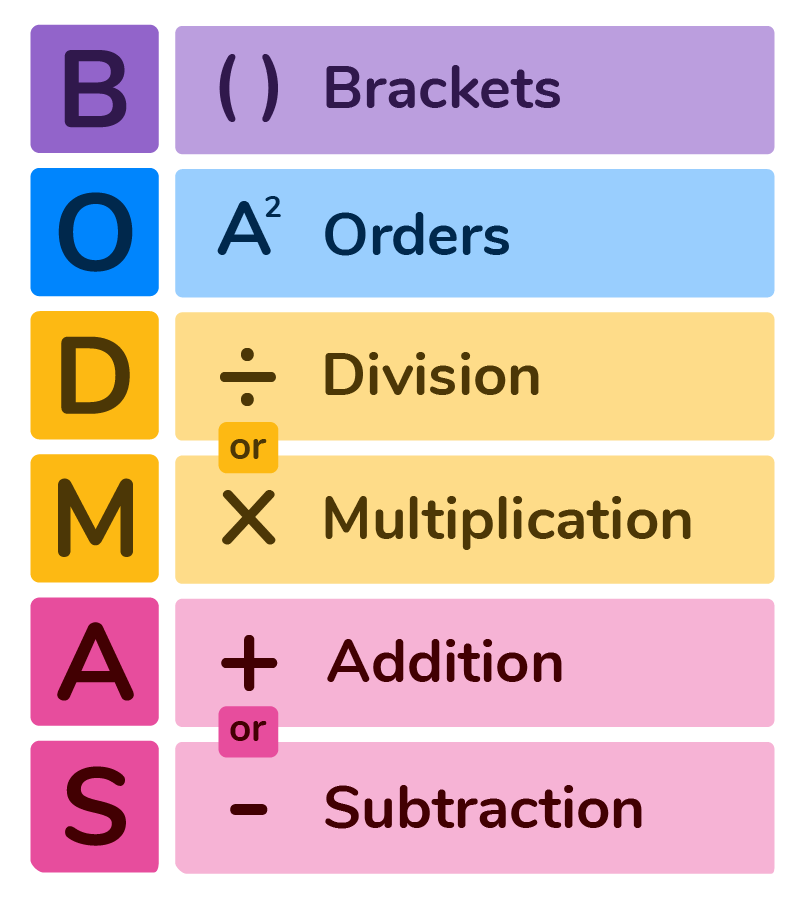
Now that we know the BODMAS meaning, let’s discuss the BODMAS Rules.
The most important BODMAS Rule is when solving order of operation questions in maths, you must follow the order of the acronym.
You may also hear the order of operations called PEMDAS. What is PEMDAS?
PEMDAS stands for Parentheses, Exponents, Division or Multiplication, Addition or Subtraction.
Parentheses are another name for brackets and exponents are another name for orders. Although the terms used for operations are different than BODMAS, both BODMAS and PEMDAS follow the same rules of order of operations.

Let’s solve this Order of Operations problem as we learn some BODMAS rules.
4² – ( 3 x 5 ) + 9 ፥ 3 x 2
1: BODMAS Rule for Brackets
When solving order of operation problems, first complete the operations that are found inside the parenthesis or brackets.
In our example problem, we would multiply 3 x 5 first because it is in the brackets.
4² – ( 3 x 5 ) + 9 ፥ 3 x 2
4² – 15 + 9 ፥ 3 x 2
2: BODMAS Rule for Orders
Orders (or powers) should always be simplified before moving to the next step in the order of operations. If you begin multiplying, dividing, adding, or subtracting while there is still an exponent in the problem, you may have missed this step.
This is how we would simplify the exponents:
4² – 15 + 9 ፥ 3 x 2
16 – 15 + 9 ፥ 3 x 2
3: BODMAS Rule for Multiplying or Dividing
When using the order of operations, you may have noticed the word “or” is used when multiplying or dividing. When following the order of operations, you can multiply or divide in any order. Simply complete the operation that comes first.
We have both multiplication and division in this problem, so we will go from left to right. First is division, then is multiplication.
16 – 15 + 9 ፥ 3 x 2
16 – 15 + 3 x 2
16 – 15 + 6
4: BODMAS Rule for Addition or Subtraction
When using the order of operations, you may have also noticed the word “or” is used when adding or subtracting. When following the order of operations in math, you can add or subtract in any order. Simply complete the operation that comes first.
In our example, we would add or subtract depending on which operation comes first.
16 – 15 + 6
1 + 6
7
Now that we know some of the BODMAS rules, let’s go over some examples together.
EXAMPLE 1: Solve 3 + ( 8 x 9 ) =
First, we see brackets come first in the BODMAS acronym. So we multiply 8 x 9 because it is in the brackets. Therefore, 8 x 9 is equal to 72. Then we would add 3 and 72 to get 75 as our answer.
Our work would look like this:
3 + (8 x 9)
3 + 72
75
EXAMPLE 2: Solve 12 ፥ 3 + 14 =
In our acronym, we see division comes before addition so we divide 12 by 3 which is equal to 4. Next, add 4 and 14 which equals 18.
Our work would look like this:
12 ፥ 3 + 14
4 + 14
18
Try DoodleMaths for free!
Select a year group
Scroll down for the answers!
1. Solve 2² + 12 – ( 3 x 2) =
2. Solve (3 x 2) + (12 ፥ 3 ) =
3. Solve 100 ፥ 10 – (6 ፥ 2 ) =
BODMAS stands for Brackets, Orders, Multiplication or Division, Addition or Subtraction.
In order of operations problems, multiplication or division can happen in any order. The official rule is to complete whichever operation comes first.
Always complete whichever operation is inside of the brackets first.
Yes. PEMDAS and BODMAS are both acronyms to represent the order of operations, but they use different words to describe the same operation. For example, PEMDAS uses the terms parenthesis and exponents. BODMAS uses the terms brackets and powers.

Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

First, multiply 3 x 2 because it is in the parenthesis. Then, simplify the exponent 2² which equals 4. Next, add 4 + 12 which equals 16. Finally, subtract 6 which equals 10.
2² + 12 – (3 x 2) =
2² + 12 – 6 =
4 + 12 – 6 =
16 – 6 =
10
First, multiply 3 x 2 because it is in the first parenthesis. Next, divide 12 by 3 because it is in the second parenthesis. Finally, add 6 + 4 which equals 10.
(3 x 2) + (12 ፥ 3 )
6 + (12 ፥ 3 )
6 + 4
10
First, divide 6 by 2 because it is in the parenthesis. Next, divide 100 by 10. Finally, subtract 3 from 10 which equals 7.
100 ፥ 10 – (6 ፥ 2 )
100 ፥ 10 – 3
10 – 3
7
Lesson credits

Amber Watkins
Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring primary through university level maths. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"

Amber Watkins
Amber is an education specialist with a degree in Early Childhood Education. She has over 12 years of experience teaching and tutoring primary through university level maths. "Knowing that my work in math education makes such an impact leaves me with an indescribable feeling of pride and joy!"
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: