

Whole numbers are a set of numbers that includes positive integers and 0. In this guide, learn everything you need to know about whole numbers!

Author
Katie Wickliff
Published
October 20, 2023


In this guide, learn everything you need to know about whole numbers!

Author
Katie Wickliff
Published
Oct 20, 2023


Whole numbers are are a set of numbers that includes positive integers and 0. This article covers everything you need to know about whole numbers!

Author
Katie Wickliff
Published
Oct 20, 2023


Key takeaways
Table of contents
0, 65, 456, 23, 4,500, 72…
While this may seem like a random set of unrelated numbers, they all have something in common.
Do you know what it is?
Each number on this list is known as a whole number!
Whole numbers are all positive integers, beginning at zero and stretching to infinity.
Decimals, fractions, and negative numbers aren’t whole numbers.
All whole numbers, except for zero, are also called ‘counting numbers’ or ‘natural numbers’.
Whole numbers can easily be represented on a number line. Whole numbers on a number line start at zero and increase by 1s at an equal distance from left to right along the line. Let’s look at the example below:
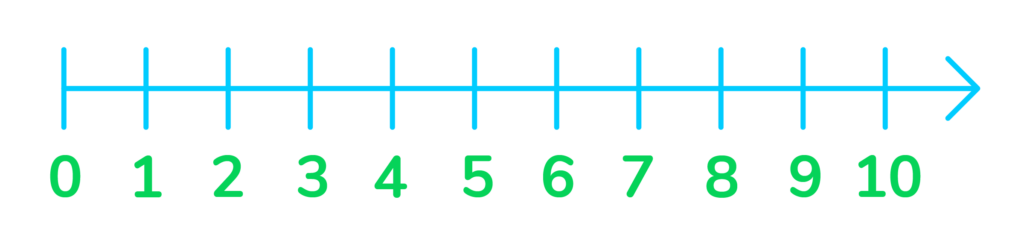
Zero is the smallest whole number, and the black arrow shows us that the whole numbers stretch on infinitely.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Try DoodleMaths for free!
Select a year group
Four properties help perform operations with whole numbers. These are:
Closure Property states that adding and multiplying two whole numbers will always have a whole number sum or product. It’s impossible to add or multiply two whole numbers and get a negative number, fraction or decimal answer.
Associative Property states that three whole numbers added or multiplied together will always have the same sum or product, no matter how the numbers are arranged. For example:
3+4+2=9
4+2+3=9
2+3+4=9
No matter how the 2, 3, and 4 are arranged, the sum will always be 9.
6x2x2=24
2x2x6=24
2x6x2=24
No matter how the 2, 2, and 6 are arranged, the product will always be 24
Commutative property states that two whole numbers added or multiplied together will always have the same sum or product, no matter how the numbers are arranged. This is the same as the associative property, except with two whole numbers instead of three. For example:
4+2=6
2+4=6
No matter how the 4 and 2 are arranged, the sum will always be 6.
3×7=21
7×3=21
No matter how the 3 and 7 are arranged, the sum will always be 21.
Distributive Property states that in an expression such as A(B+C), you can distribute A to each of the addends (B and C) and multiply them then add the two products together: (AB)+ (AC). Here’s a whole numbers example of this property:
5x(2+3)=25
You can solve this by adding the 2+3 together first and then multiplying that answer by 5 to reach the product of 25.
However, if you use the distributive property, you’d solve like this:
5x(2+3)= 5×2 + 5×3= 25
So, whether you add the numbers in parenthesis before or after multiplying, the answer will be the same!
Want to learn more about whole numbers? DoodleMaths is an app that’s filled with fun games and exercises exploring the whole primary maths curriculum!
Designed to be used ‘little and often’, it creates each child a unique work programme tailored to their needs, boosting their confidence and ability in maths.
Best of all, it’s filled with tips and sets work at just the right level, letting your child work independently. Try it for free today!


Click on the boxes below to reveal the answers!
92, 93, 94
True
There are 11 whole numbers between 33 and 45. They are: 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44.
C
No, negative numbers are not whole numbers.
Positive integers are whole numbers. However, negative integers are not whole numbers.
Yes, 0 is a whole number.


Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Lesson credits

Katie Wickliff
Katie holds a master’s degree in Education from the University of Colorado and a bachelor’s degree in both Journalism and English from The University of Iowa. She has over 15 years of education experience as a K-12 classroom teacher and Orton-Gillingham certified tutor. Most importantly, Katie is the mother of two elementary students, ages 8 and 11. She is passionate about math education and firmly believes that the right tools and support will help every student reach their full potential.

Katie Wickliff
Katie holds a master’s degree in Education from the University of Colorado and a bachelor’s degree in both Journalism and English from The University of Iowa. She has over 15 years of education experience as a K-12 classroom teacher and Orton-Gillingham certified tutor. Most importantly, Katie is the mother of two elementary students, ages 8 and 11. She is passionate about math education and firmly believes that the right tools and support will help every student reach their full potential.
How to improve at mental maths
Learn some handy mental maths strategies that’ll make addition a breeze!
A guide to the KS1 maths curriculum
Discover all the topics children are introduce to in KS1 maths
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: