Dealing with fractions can be difficult, and dividing fractions is no different. Let’s learn how to divide fractions in 5 easy steps.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: January 23, 2024


Dealing with fractions can be difficult, and dividing fractions is no different. Let’s learn how to divide fractions in 5 easy steps.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: January 23, 2024




Dealing with fractions can be difficult, and dividing fractions is no different. Let’s learn how to divide fractions in 5 easy steps.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: January 23, 2024


Key takeaways
Fractions are already parts of a whole number. So, you might be wondering: how can you divide a fraction into an even smaller part—or, for that matter, divide it to turn it into an even bigger part?
Honestly, it works the same way dividing whole numbers works. You can divide a small number into an even smaller number, right? Four divided by 2 gives you 2. So how can ¼ divided by ½ give you ½? Today, we’re going to walk through how to divide fractions in 5 easy steps. But first, let’s make sure we understand the basics to make it super easy to follow along.
Unlike a whole number, a fraction has two parts.
Visually, 1⁄4 would look like this, with 1 out of 4 parts shaded in.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!


There are several different ways to divide fractions, but if you try to master them or use them all at once, it might get super confusing. It’s always best to divide complicated ideas into smaller parts to make the ideas easier to understand. Let’s DIVIDE (ha, see what we did there?) dividing fractions into five easy steps to help make it easier.
It might sound simple, but first, you need to understand what you’re being asked to do. Let’s look at the following problem:

Basically, you’re being asked to divide five-sixths by seven-eighths.
Next, you need to know what to do with each of the fractions in the problem. Do not do anything to the first fraction. Keep it EXACTLY as it is.

You mean I have to know how to multiply to know how to divide? Absolutely you do! What you want to do in this step is to change the DIVISION sign to a MULTIPLICATION sign.
So, if we were just rewriting the problem and this was our final step, the problem would look like this:

But it ISN’T the last step. The last step is…
The last step before you can solve the problem is to flip the numerator with the denominator in the second fraction. So, now your problem looks like this:
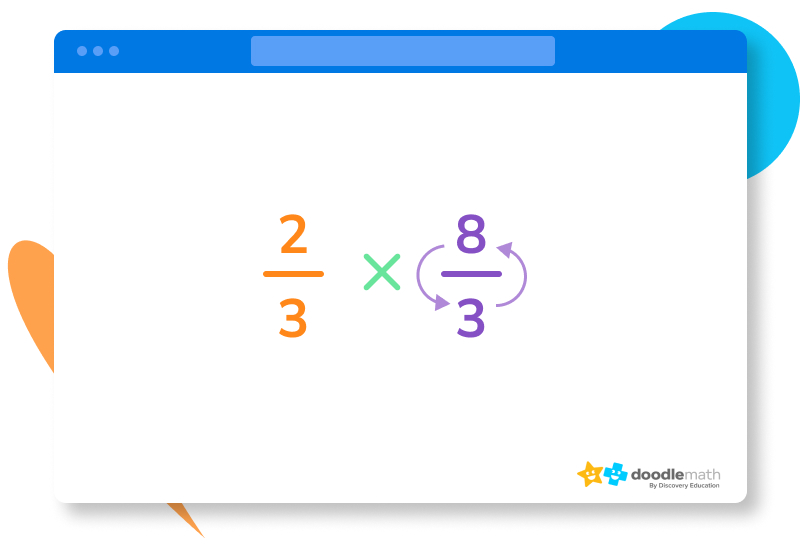
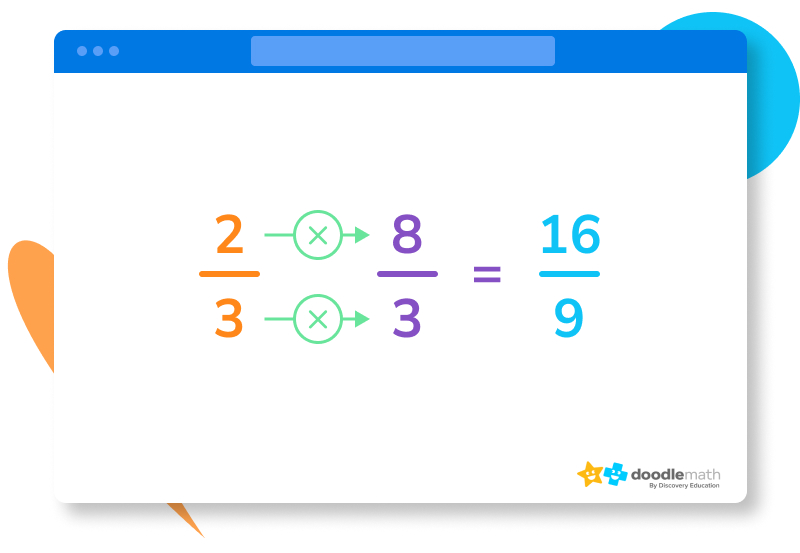
The answer is 16⁄9, which cannot be simplified, so it remains the same. Take your problem a step further by converting your answer into a mixed number which is 1 7⁄9.
Want to learn more about dividing fractions? DoodleMaths is an award-winning app that’s filled with questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!


Click to reveal the answer.
The answer is 15⁄6, and since both 15 and 6 can be divided by 3, the answer, when simplified, will be 5⁄2.
How did we get here?
The answer is 16⁄15. This cannot be simplified, as these numbers cannot be divided by a similar number.
How did we get here?
The answer is 4⁄3. This is simplified from 24⁄18, numbers that can each be divided by 6 to give you 4⁄3.
How did we get here?
The answer is 12⁄7. This cannot be simplified, as these numbers cannot be divided by a similar number.
How did we get here?
The answer is 7⁄4, simplified from 14⁄8, which can both be divided by 2 to give you the answer.
How did we get here?
Sign up for the DoodleMaths app today!
Turn maths into an adventure when you sign up for DoodleMaths.
If the divisor is a whole number, you can convert it to a fraction by putting it over 1. For example, if you want to divide 3⁄4 by 2, you can rewrite it as 3⁄4 ÷ 2⁄1. Then, you proceed with the division using the reciprocal: (3⁄4) × (1⁄2) = 3⁄8.
Yes, the dividend can be a whole number! In division, the whole number is treated as a fraction with a denominator of 1. For example, if you want to divide 2 by 3⁄4, you can rewrite it as 2⁄1 ÷ 3⁄4. Then, you proceed with the division using the reciprocal: (2⁄1) × (4⁄3) = 8⁄3.


Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: