

Calculating the volume of objects has many real-world applications. Students use specific formulas to calculate the volume of three dimensional shapes.

Author
Katie Wickliff
Published
January 2024


Calculating the volume of objects has many real-world applications. Students use specific formulas to calculate the volume of three dimensional shapes.

Author
Katie Wickliff
Published
January 2024


Calculating the volume of objects has many real-world applications. Students use specific formulas to calculate the volume of three dimensional shapes.

Author
Katie Wickliff
Published
January 2024


Key takeaways
Table of contents
Whether you’re measuring the ingredients to bake a cake, adding potting soil to a gardening bed, or simply filling your water bottle before a hike, knowing how to measure volume is an essential part of our daily lives.
In this article, we’ll cover the basics of volume and include the formulas to calculate the volume of common shapes. We’ll also include practice problems for each type of shape, to give your student practice using these formulas. For even more practice, head over to our award-winning maths app. Let’s get started!
Simply put, volume is the measurement of how much space something takes up. In a three dimensional (3D) object, such as a pyramid or cone, volume is also often referred to as “capacity.” In a two-dimensional object, volume is known as “area.”
Students learn how to calculate volume by using equations. These equations vary by shape. When your student is first learning to calculate volume, they’ll start by learning to calculate the volume formulas of common 3D shapes, such as these:
To calculate the volume of a cylinder, we need to know the height of the cylinder and the radius of the base. We also need to know the approximate value of “pi,” a measurement used with circular shapes.
Pi= 3.14 which is represented as π in formulas.
Volume= πr2h
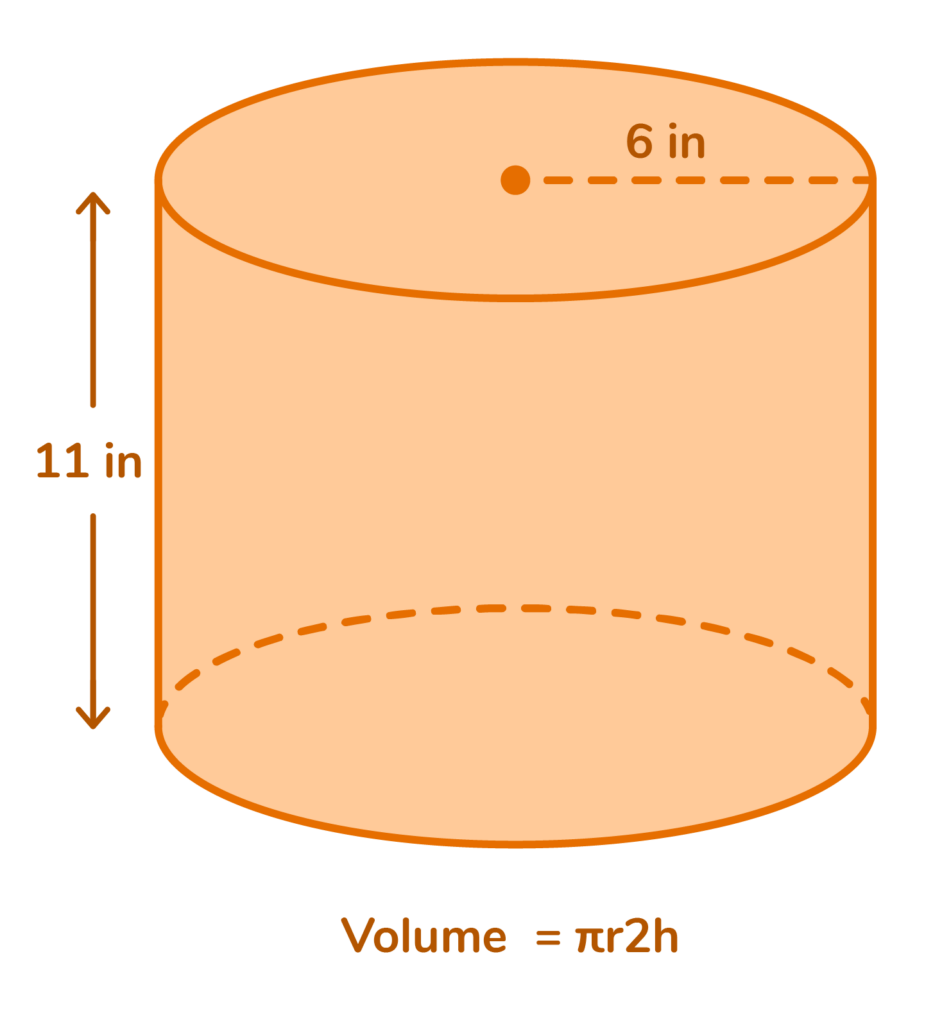
In this example, the radius “r” is 6 inches, and the height “h” is 11 inches.
V= π (6)²(11)
V= π (36) (11)
V= π 396
V= (3.14) (396)
V= 1,243.44 in³
When working with volume, we always use cubic unit measurement, which is represented by “³”
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
Want to learn more about volume? DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring quantities, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!


To find the volume of a cone, we need to know the height and the radius of the base. Just like with the volume of a cylinder (shown above) we also need to know the approximate value of “pi”.
To find the volume of a cone, we use this formula:
Volume= ⅓ πr²h
When calculating the volume of a sphere, we need to know the radius. Just like with cylinders and cones, we also need to know the approximate value of Pi.
To find the volume of a sphere, we use this formula:
Volume = 4/3 πr3
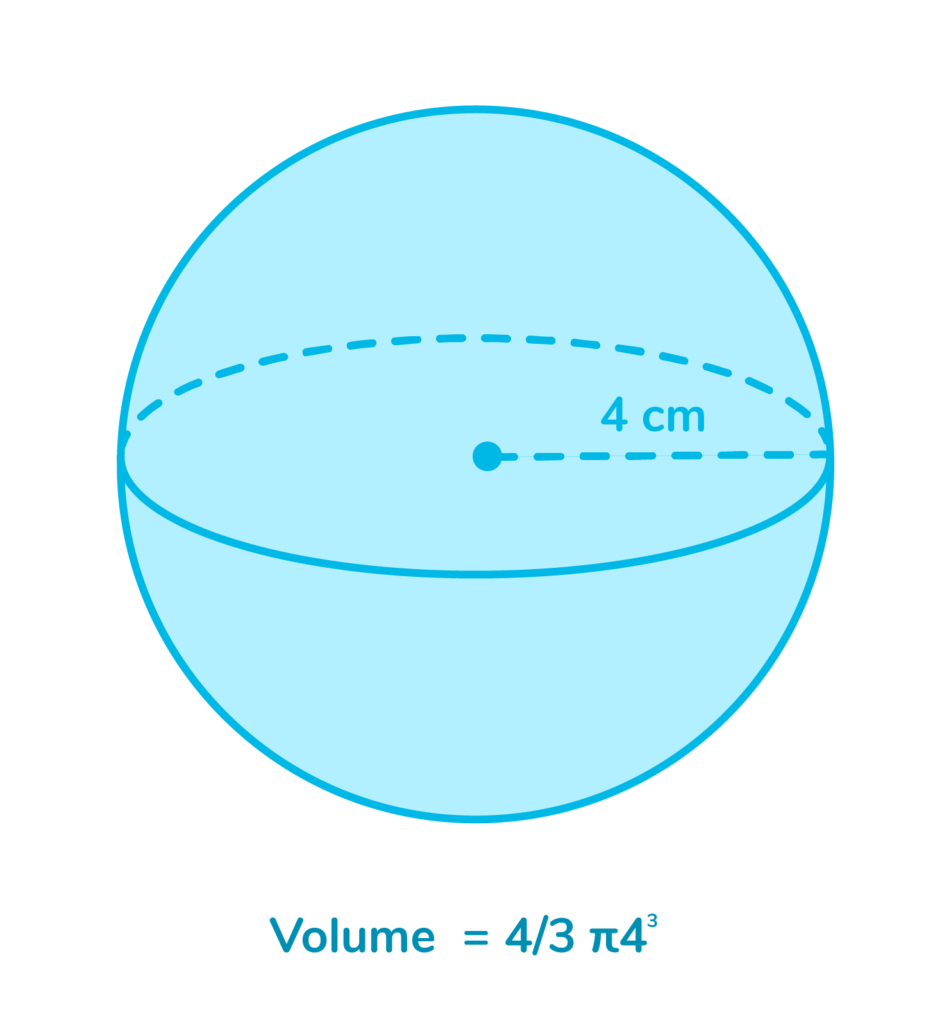
In the example above, the radius is 4 cm.
Volume = 4/3 π4³
V= 4/3 π64
V= 4/3x 64xπ
V= 85.33π
V= 267.94³
To calculate the volume of a rectangular prism, we need to know three measurements: the length(l), the width(w), and the height(h).
To find the volume of a rectangular prism, we use this formula:
Volume= length x width x height

Volume= 1 x 3 x 2
Volume= 6 ft³
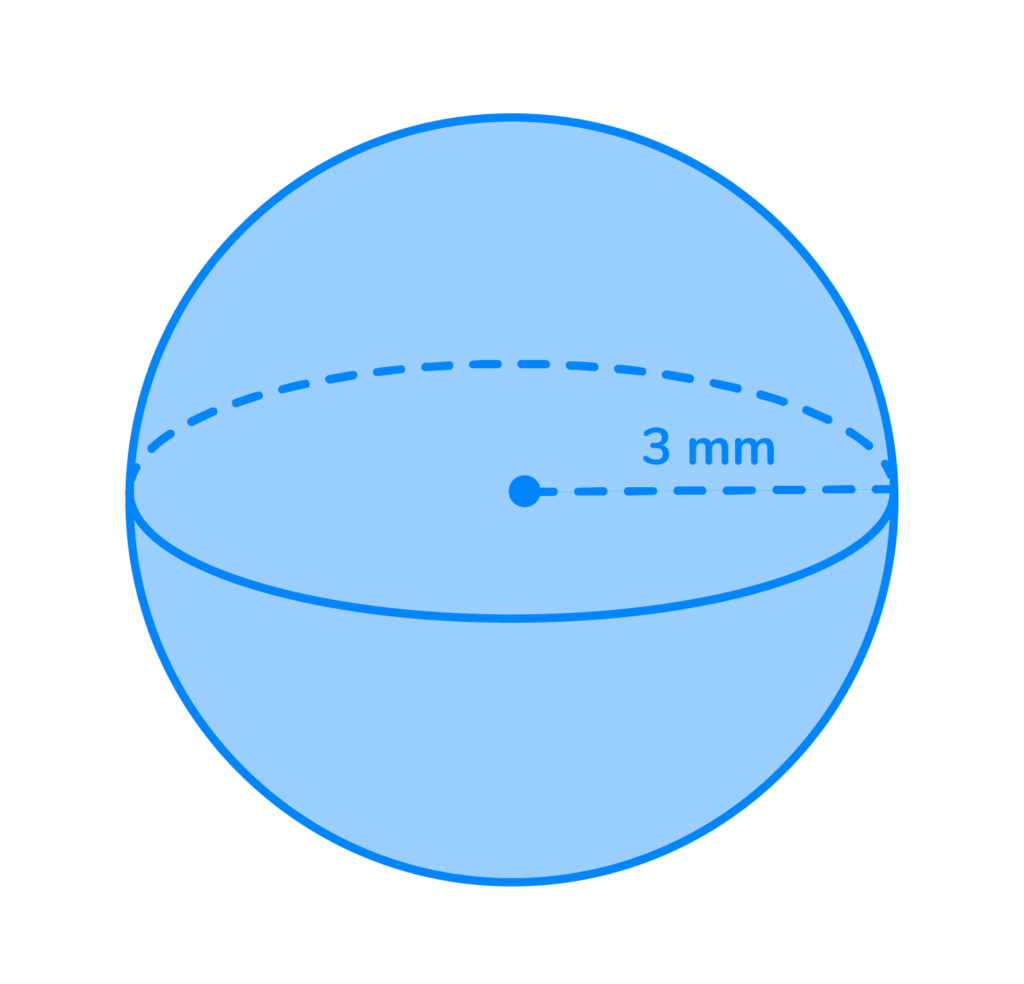
Find the volume of the sphere. Use 3.14 for π.
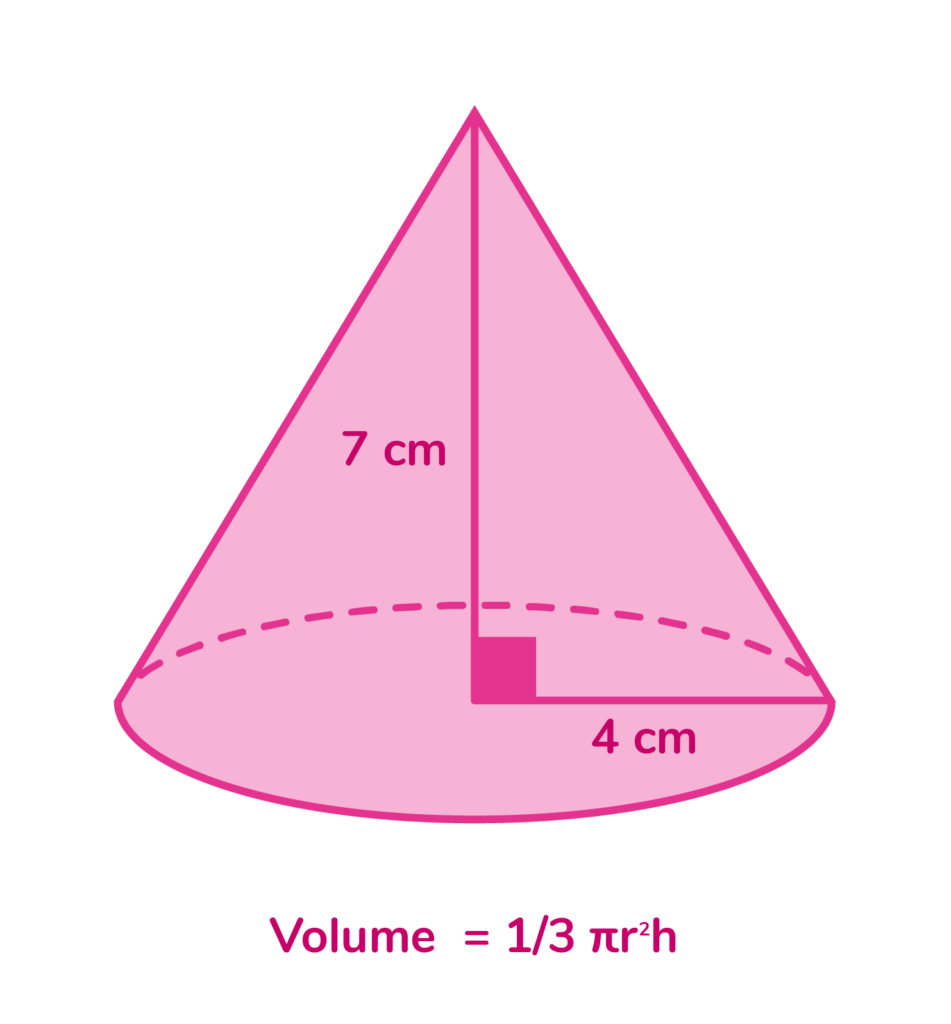
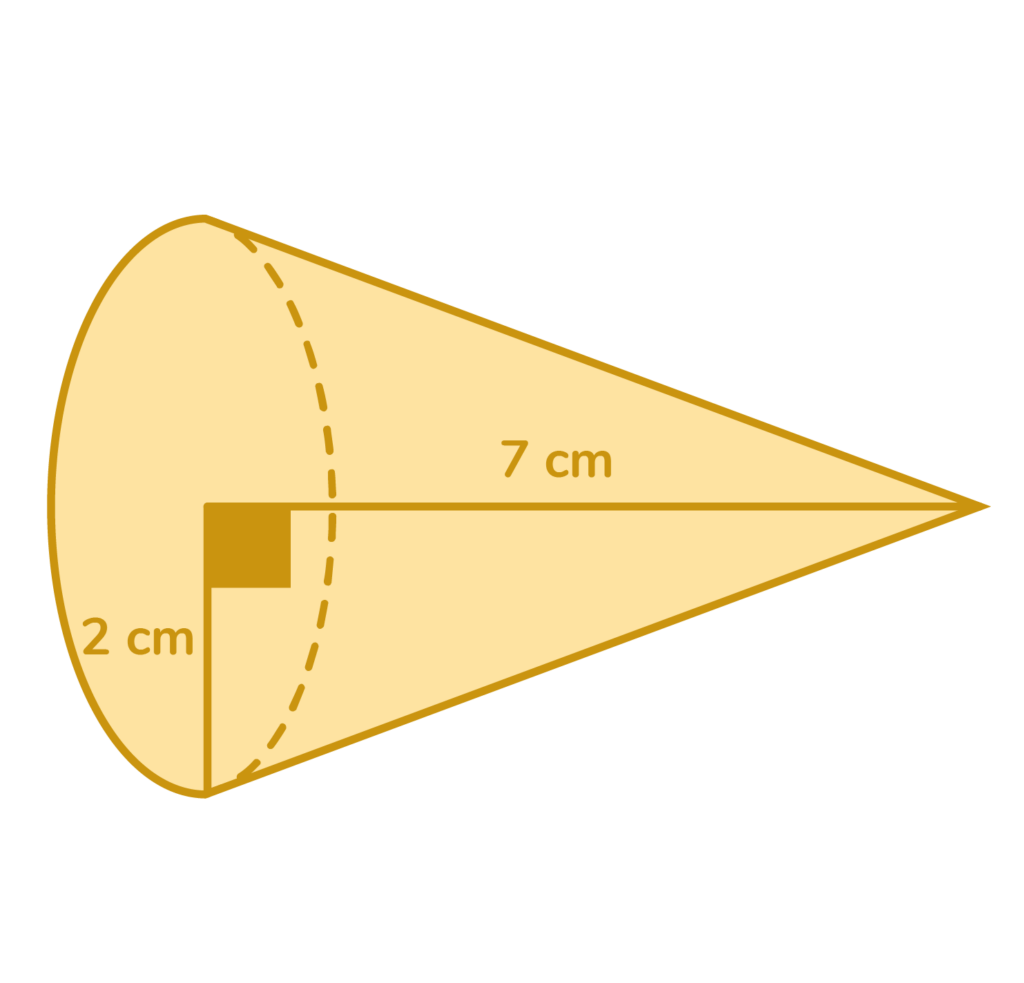
Find the volume of the cone. Use 3.14 for π
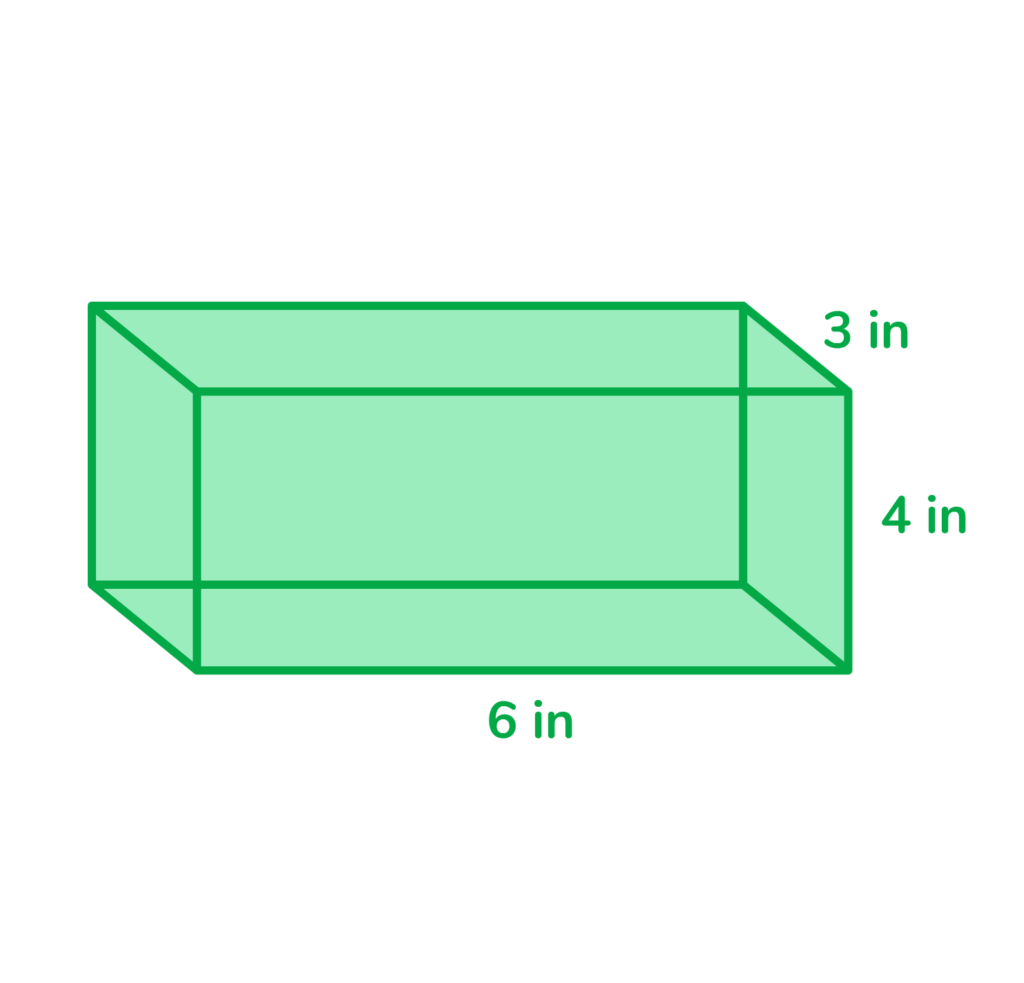
Find the volume of the rectangular prism.
A drawer is 4 feet long, 2 feet wide, and 3 feet high. What is the volume of the drawer?
Volume= 4/3π3³
Volume= 4/3π27
V= 4/3 x 3.14 x 27
V= 113.04mm³
V= ⅓ π (2)²(7)
V= ⅓ π (4) (7)
V= ⅓ π 28
V= (⅓)(3.14) (28)
V= 29.3 cm³
Volume= 4 x 6 x 3
V= 72in³
V= 4x2x3
V=24ft³
The definition of volume in maths is the amount of space an object takes up.
We measure volume by using formulas that differ based on the shape of the object.
Volume formula differs based on the type of shape. When measuring the volume of a cylinder, use the formula v= πr²h. To find the volume of a cone, use the formula volume= ⅓ πr²h. To find the volume of a rectangular prism, use the formula v= l x w x h. To find the volume of a sphere, use the formula v= 4/3 πr3


Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Lesson credits

Katie Wickliff
Katie holds a master’s degree in Education and a bachelor’s degree in both Journalism and English. She has over 15 years of experience as a teacher and is also a certified tutor. Most importantly, Katie is the mother of an 8 and 11-year-old. She's passionate about education and firmly believes that the right tools and support can help every child reach their full potential.

Katie Wickliff
Katie holds a master’s degree in Education and a bachelor’s degree in both Journalism and English. She has over 15 years of experience as a teacher and is also a certified tutor. Most importantly, Katie is the mother of an 8 and 11-year-old. She's passionate about education and firmly believes that the right tools and support can help every child reach their full potential.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: