Learn about lines of symmetry and how they are used in geometry.
Author
Gary Ferguson
Updated
May 2024
Learn about lines of symmetry and how they are used in geometry.
Author
Gary Ferguson
Updated
May 2024
Learn about lines of symmetry and how they are used in geometry.
Author
Gary Ferguson
Updated
May 2024
Key takeaways
Knowing what symmetry is isn’t just useful for school: it can also help you to create aesthetically pleasing designs! In this article, you’ll learn what symmetry is and how it can be used to create beautiful artwork.
A line of symmetry is a line that splits a design in half so that both of the halves are symmetrical (look the same on both sides).
To create a line of symmetry, you need an anchor point. This is the point where the two halves of the design meet. The anchor point can be anywhere on the line of symmetry, but it’s usually in the middle!
There are lots of reasons why symmetry is helpful. One of the most important is that symmetry creates balance. Our brains really like symmetrical things and are automatically drawn to it.
Another reason is that it makes things much easier to understand. Symmetrical objects are predictable, so we know what to expect, making them easier to remember.
Lastly, symmetry is aesthetically pleasing to us. We tend to find symmetrical objects attractive and harmonious. This may be because symmetry exists throughout nature and reminds us of some of our most beautiful creations in life.
Get 1 FREE month of Doodle!
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Try DoodleMaths for free!
Select a year group
There are many ways to create a line of symmetry, but the most common way is by using a ruler.
To create a diagonal line of symmetry, you can fold the paper in half diagonally. Then, once you’ve found the centre, you can draw a line from one corner to the other: you’ve now discovered your diagonal line of symmetry!
Lots of shapes have lines of symmetry, but some shapes have more than others.
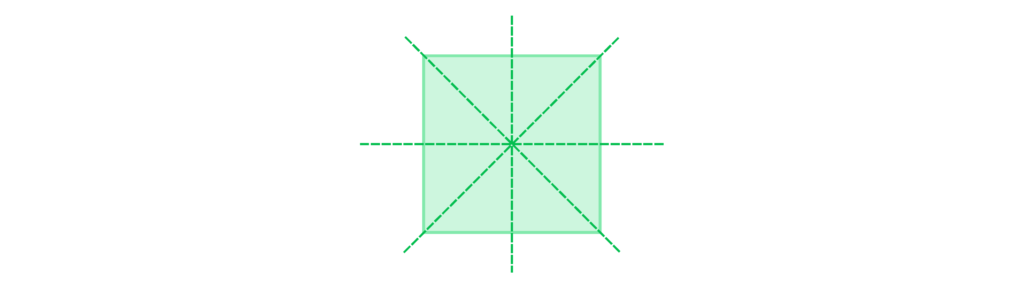
For example, a square has four lines of symmetry (one horizontal, one vertical, and two diagonal). On the other hand, some shapes have no lines of symmetry. For example, a circle and oval both have no lines of symmetry, because they’re symmetrical all around their centres!
Here’s a quick guide to how many lines of symmetry the most common 2D shapes have.
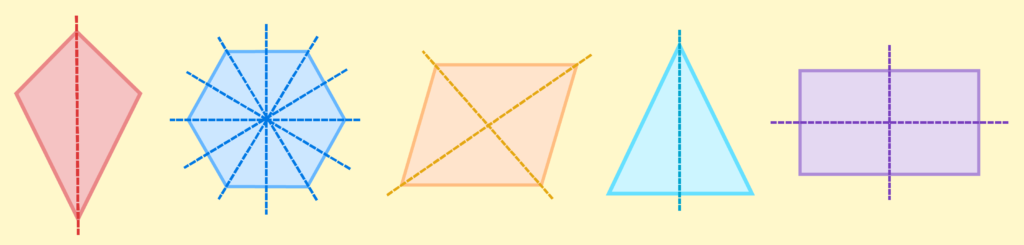
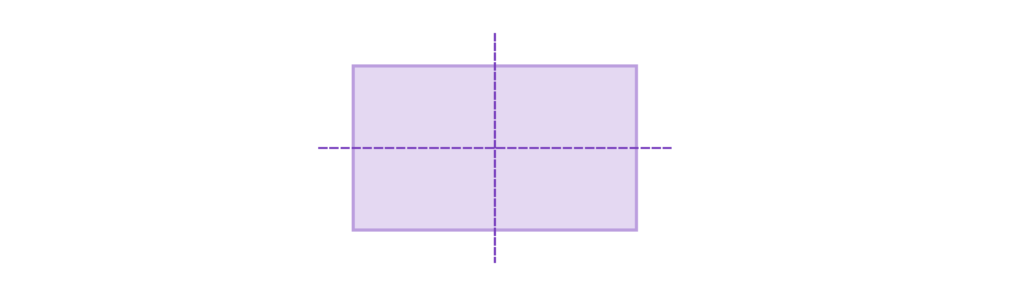
A rectangle has two lines of symmetry: one horizontal and one vertical.
A square has four lines of symmetry: one horizontal, one vertical, and two diagonal.
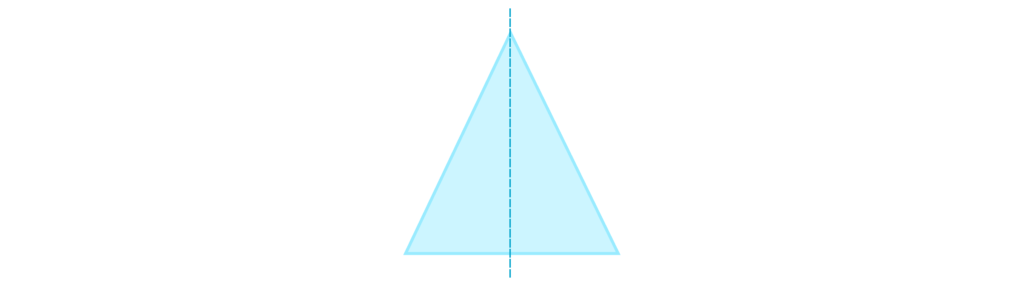
A triangle has one line of symmetry: the line that bisects the triangle.
A parallelogram has no lines of symmetry.
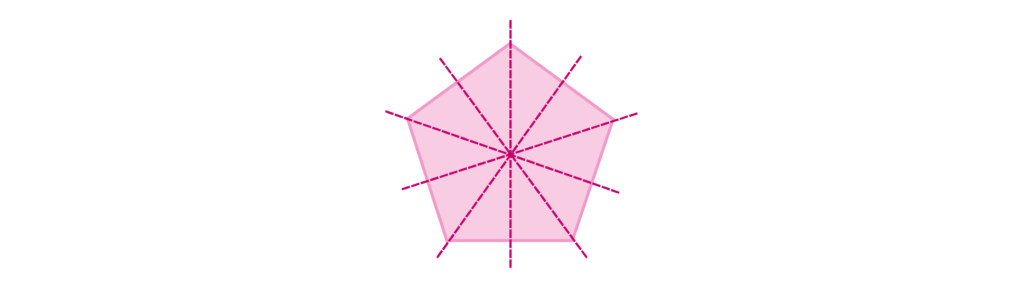
A pentagon has five lines of symmetry: one horizontal, one vertical, and three diagonal.
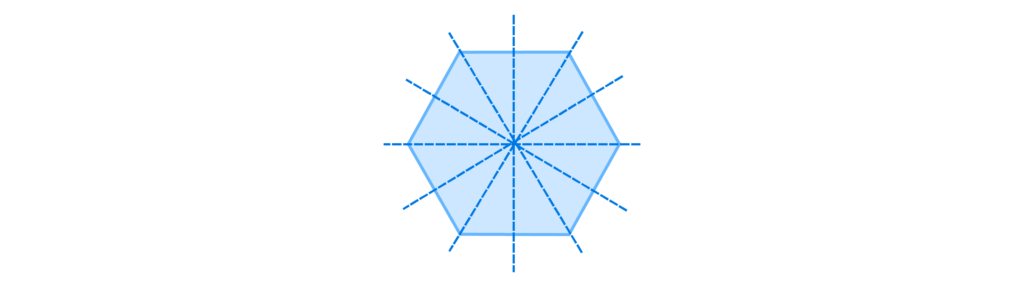
A hexagon has six lines of symmetry: one horizontal, one vertical, and four diagonal.
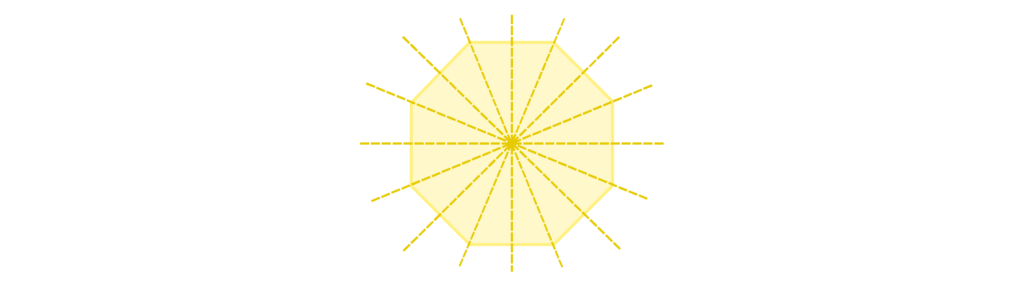
An octagon has eight lines of symmetry: four horizontal and four vertical.
A circle has no lines of symmetry because it is symmetrical all around its centre.
A kite has one line of symmetry: one vertical.
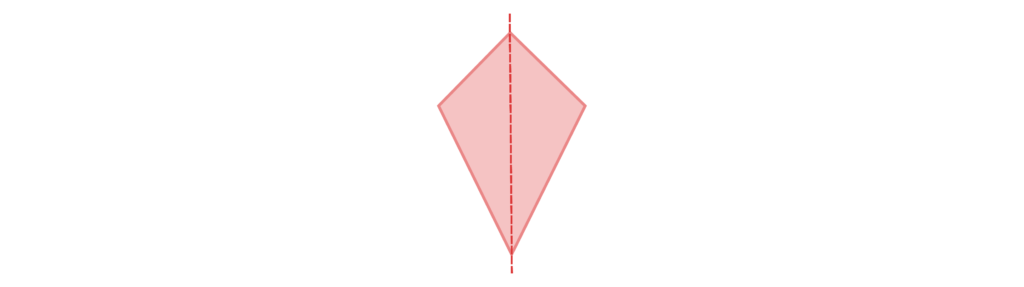
A rhombus has two lines of symmetry: two diagonal.
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!
Rotational symmetry is where a design repeats itself, creating a symmetrical pattern.
Looking for a way to explore symmetry with your pupils or child? Here are some activities and games you can enjoy in the classroom or at home:
By using the above techniques for standard and rotational symmetry, you can create your very own beautiful, symmetrical designs.
In addition, being able to identify lines of symmetry can help you in many areas, from art to mathematics. We hope that this article has helped you learn more about lines of symmetry and given you some ideas for fun activities to explore with your children or pupils!
Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
