In this guide, learn how to identify and measure one of the most important and common shapes in maths – a square!

Author
Taylor Hartley

Expert reviewer
Jill Padfield
Published: August 24, 2023


In this guide, learn how to identify and measure one of the most important and common shapes in maths – a square!

Author
Taylor Hartley

Expert reviewer
Jill Padfield
Published: August 24, 2023




In this guide, learn how to identify and measure one of the most important and common shapes in maths – a square!

Author
Taylor Hartley

Expert reviewer
Jill Padfield
Published: August 24, 2023


Key takeaways
Squares are everywhere — and they’re pretty easy to spot once you can recognise the shape! It’s important to understand the must-have principles that a shape needs to be a square, though. So, let’s learn all about squares!
A square is a regular polygon with four equal sides and equal angles that each measure 90°.
For a quick refresher, a regular polygon is a two-dimensional enclosed figure made by joining three or more straight lines. Now, let’s identify some real world examples of squares!
You come across squares every day, and you might not even realise it!
Everyday items like picture frames, sticky notes and pizza boxes are just a few examples. Take a look at the images below for some visual examples, then take a look around your room — can you identify three square-shaped objects?

Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
There are certain properties that a shape must have in order to be a square. Keep an eye out for the following must-haves to determine if something is a square:
Try DoodleMaths for free!
Select a year group
The best way to learn anything is to break it down into its parts — it’s so much easier to understand! Let’s take a look at the three different parts of a square.
The length of a square is best described as the top and bottom lines of the square, as shown below.
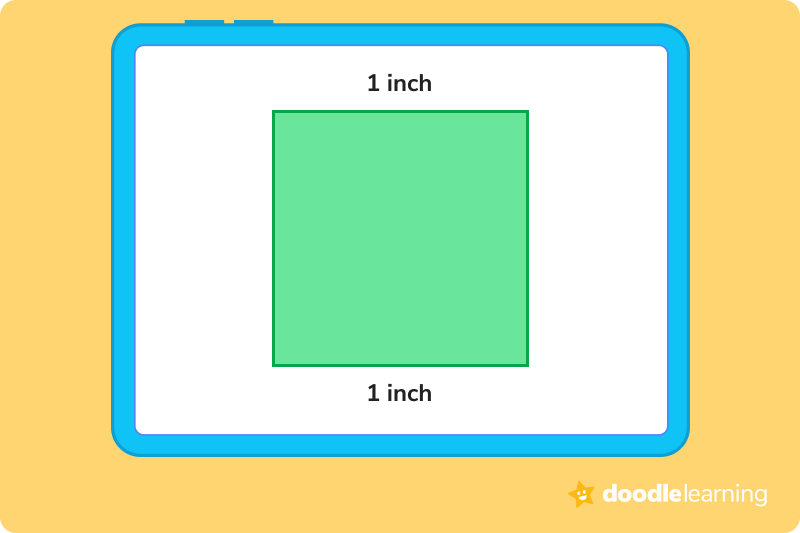
The width of a square is simply the left and right-hand sides of a square, as shown below.

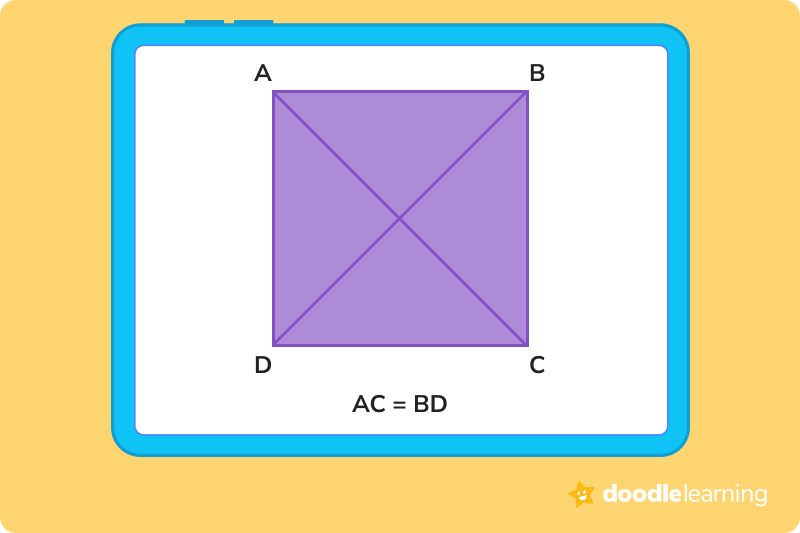
The diagonal of a square is a line that connects one corner to the opposite corner through the center, as shown below. A square has two diagonals that are equal in length, and they bisect each other at right angles.
Once you’ve identified that something is a square, then you can measure it! We can measure the area and the perimeter of a square with two easy formulas.
The perimeter of a square is the length of the outer boundary of the shape. For a square of side length “S” units, the perimeter is presented as the following formula:
Perimeter = side + side + side + side = 4 × S
The perimeter of a square is expressed in linear units like centimeters (cm), inches (in), meters (m), etc.
The area of a square is the amount of space covered by the shape if we were to keep it on a flat table. For a square of side length ‘S’ units, the area is presented as the following formula:
Area = side × side = S2
The area of a square is expressed in square units like cm2, m2, etc.
DoodleMaths is an award-winning app that’s filled with thousands of interactive questions and games exploring shape, measurement and more!
Designed to be used ‘little and often’, its powerful algorithm creates each child a unique work programme tailored to their needs, boosting their skills in as little as six weeks.* Try it free today!

*Based on earning 24 stars a day in DoodleMaths. Read full study
1. Identify the square in the following group of shapes:
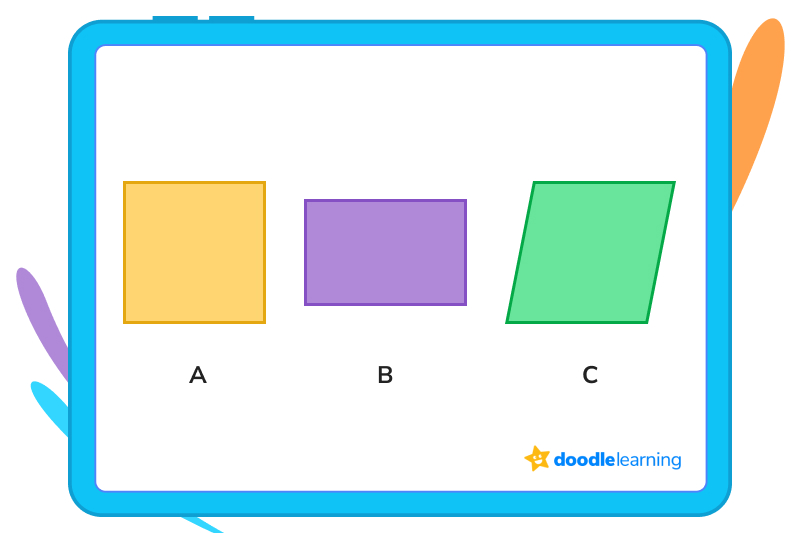
The correct answer is A. Figure A has equal sides and interior angles that all measure 90°. Figure B is a rectangle, with its length different from its width, and C is a parallelogram, with interior angles that do not equal 90°.
2. Find the perimeter of a square that has four sides measuring 5 inches each.
Remember, each side of a square is equal to the other side. That means we have 4 sides that equal 5 inches. So the perimeter is 5 + 5 + 5 + 5 or 4 × 5, which equal 20 inches.
3. Find the area of a square that has four sides measuring 11 cm each.
The area of a square is the measure of its length × its width. So, if we multiply 11 × 11, we get 121 cm2.
Ready to give it a go?
Now that you know how to identify a square, the parts of a square and how to measure them, we’re ready to do a few practice questions!
Work through the following problems on your own. Feel free to look back at the practice problems above if you get stuck, or if you need a quick reminder on what a square is or how to measure its parts.
And remember, don’t get discouraged if you run into a roadblock! Practice is the best way to learn something new.
Click to reveal the answer.
The area is 64 sq. ft.
The perimeter is 24 inches.
The perimeter is 48 inches.
The area is 625 sq. cm.
The measure of its side is 14 cm.
What makes a square a square is how equal its sides are. To be a square, a polygon must have four sides of equal length and four right angles. All squares are rectangles, but not all rectangles are squares.
Why? Because the length of a rectangle doesn’t have to equal its width. To be a square, all sides have to be equal.
To measure the area of a square, simply multiply its length and its width. For example, say you have a square with sides that equal 4 inches. You would multiply 4 by 4 to get 16 inches.
Squares are important because they play a major role in construction, decoration, and artistic expression. They are one of the few shapes that can fit together perfectly, making them the best choice for projects like tile floors or roof shingles.
Without squares, we also wouldn’t have fun board games like Monopoly or CandyLand, where you have to land on squares to move forward. And we can’t forget Four Square, one of the best games to play with friends!
In exciting fields like design, many people say that the square represents strength and stability. This is because of its equal sides and equal angles. Some psychologists say that many people associate the square with truth and consistency, since it is uniform all the way around.

Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

The area is 64 sq. ft.
How did we get here?
The perimeter is 24 inches.
How did we get here?
The perimeter is 48 inches.
How did we get here?
The area is 625 sq. cm.
How did we get here?
The measure of its side is 14 cm.
How did we get here?
Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
What are parallel lines?
Learn all about parallel lines, including what they look like and their definition
3D shapes: names and properties
From spheres to cubes, we explore everything you need to know
What is a rhombus shape?
In this guide, discover the key properties of this unique four-sided shape!
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: