What is division in maths?

Division is a superpower that breaks down a whole — whether you’re cutting a pizza or divvying up playing cards!

Author
Christina Levandowski

Expert Reviewer
Jill Padfield

Published: August 24, 2023

What is division in maths?

Division is a superpower that breaks down a whole — whether you’re cutting a pizza or divvying up playing cards!

Author
Christina Levandowski

Expert Reviewer
Jill Padfield

Published: August 24, 2023

What is division in maths?

Division is a superpower that breaks down a whole — whether you’re cutting a pizza or divvying up playing cards!

Author
Christina Levandowski

Expert reviewer
Jill Padfield

Key takeaways

Division is an opposite game: if you multiply numbers, you can ‘undo’ them using division. It’s multiplication’s opposite function!
There are a few signs to look for: there are three main symbols for division.
You won’t always get ‘even Stevens’: sometimes you’ll have a little left over. That leftover number is known as the ‘remainder’.

Table of contents

Division is one of the most important maths skills you’ll learn, helping you to undo multiplication problems or break off parts of a ‘whole’.

We know it looks complicated, but it really isn’t! You just need to know what signs to look for that tell you when division is needed.

Like addition and subtraction, division uses a few special terms and symbols. Knowing these can help you to work out your problems quickly and correctly.

With a little practice and this handy guide, you’ll be flying through your maths homework in no time! Let’s get started.

Unlock unlimited maths questions

Put your learning into practice with fun exercises + games that are proven to boost ability!

Get 2 FREE weeks of Doodle!

Use code 2WKS_AUTUMN to enjoy unlimited questions and games

What is division?

Division is a process in maths that lets you break down a number into multiple, equal parts.

Sometimes, you can cut everything down into whole number parts, and sometimes you’ll be left with a little leftover, giving you a decimal or fraction for an answer rather than a whole number.

You’ll often see division problems vertically, like this:

It can also be written horizontally: 10 ÷ 2, as 10/2 , or using a division bar: 2 ⟌ 10.

No matter how you see it, though, the use for it is always the same. You’re breaking down a number or quantity into smaller pieces.

Let’s take a look at some key terms that’ll help you build your division skills.

Use code 2WKS_AUTUMN to get 2 FREE weeks of Doodle!

Common division symbols and terminology

Division is a simple mathematical operation, but there are still a few terms to know to help you find the correct solution.

Here are the terms you need to know to solve division equations with ease:

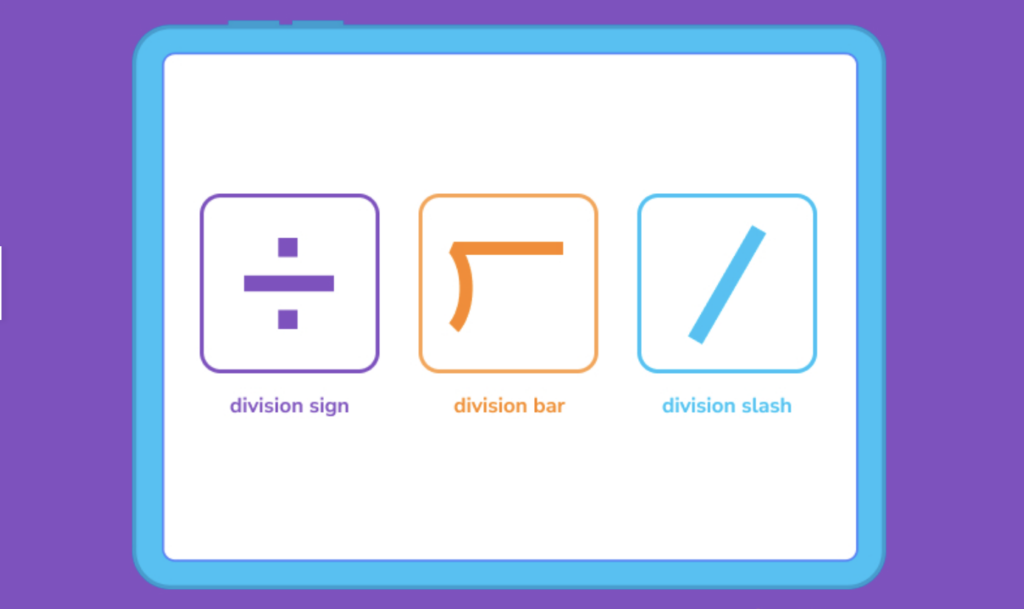
Division symbols

➗ — This is known as a division sign, and it tells you that a number needs to be broken down into multiple pieces.

⟌ — This is the division bar, and it also means to divide. On the outside of the bar, you’ll see the number determining how many pieces are needed from the whole (the divisor), and the dividend on the inside, which is what you’ll be dividing. The answer goes on the top of the bar.

∕ — This is known as the division slash. Generally, the divisor comes first, and the dividend will appear second.

Important division vocabulary

Knowing these terms will help you to know what numbers you’re dividing and how you should set up and read your equations. There are four main terms to know as you work through your arithmetic operations.

Divisor – The divisor is the number that is determining how many pieces are needed from the whole. For example: in 15 ÷ 3, three would be the divisor. It’s also the number located outside of the bracket when you see a division bar.
Dividend – The dividend is the number that’s being divided, and it’s found inside the division bar.
Quotient – The quotient is your answer, which goes after the equals (=) sign or on the top of the division bar.
Remainder – In some cases, you’ll have a remainder — which means that the divisor can’t be equally divided into the dividend. The remainder is written to the side of your equation next to the division bar.

Explore division with DoodleMaths

DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!

Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!

Create a free Doodle account

Properties of division

Anytime you see the word ‘property’ in maths, know that it’s just a rule to remember as you work through your groups of problems. Here are some of the most important properties of division that you need to know:

The division by 1 property: If a number is divided by 1, the quotient will always be the original number.
The division by itself property: If a number is divided by itself, the quotient will always be 1.
The division by 0 property: If a number is divided by 0, it’s “undefined” and cannot be solved.
The division of 0 By (any) number property: If a 0 value is divided by any number, you’ll have 0 as your quotient.

Knowing these helpful properties can help you to do basic operations (like division) confidently. Remember — these are division facts, so these properties will always be true…no matter what problem you’re working to find the quotient to!

How to divide in 6 easy steps

Now that you know the terms and properties of your division operation, it’s time to practice your skills. Let’s work the problem below together.

15 3

1. Prepare your equation

We know that the problem above can feel overwhelming — so we want to take this moment to remind you that what we’re doing is breaking down a number into smaller numbers (or smaller groups of numbers).

First things first, we have to prepare the equation. Feel free to keep it horizontal, write it vertically, or use a division bar if you’d like. Use whatever method you feel comfortable with.

Remember: The dividend (15) belongs inside the division bar if you choose to use that method.

2. Start with the first digit of the dividend from the left

As we begin to divide, we need to start from the first digit from the left (in this case, 1) and ask ourselves: Does the divisor (3) go into 1 at least once?

The answer here is “no,” so we will then evaluate the first AND second integer (making 15) as a dividend.

We ask again: Does the divisor (3) go into 15 at least once?

Now, the answer is “yes” — we just have to count how many times 3 can go into 15, starting our division process.*

NOTE: You can do this by using basic arithmetic operations (such as multiplication) to ‘undo’ the problem (i.e., 3 x ? = 15) or counting by threes until you reach 15.

In our case, 3 goes into 15 a total of five times.

3. Divide it by the divisor and write the answer on top as the quotient

Now that we know that 15 ÷ 3 = 5, it’s time to write it into our equation. Go ahead and write 5 behind the equals sign or standing tall at the top of your division bar.

4. Subtract the product of the divisor and the digit written in the quotient from the first digit of the dividend

Now, we have to check our work. We have to ask ourselves: what is 5 x 3? Does it equal our dividend? If it does, you’re golden — you’ve done it!

Do the multiplication, and then subtract your product to ensure that there’s no other steps remaining (like you’d see in the case of a remainder).

In our example, 15 – 15 = 0…so no remainder or further action is needed.

5. Bring down the next digit in the dividend (if possible)

In other problems, if you did have a three or four digit dividend, you might need to bring down the next digit in the dividend, and determine if your divisor divides that number cleanly.

You would then repeat the division process, putting your answer over the third or “next” place above the division bar as part of the quotient.

Next, yo would repeat step 4 to determine if more steps in the division process are needed.

In our example, we don’t have to do this, so we will leave it as is. Good work!

6. Repeat

Congratulations! You just broke a large number down into equal, separate parts. It’s time to repeat the process for your other problems.

What is long division?

Long division is a form of division that’s used to break down larger numbers and will generally repeat steps 1-6 above at least three or more times.

We’ll work on that stuff later — for now, let’s just focus on mastering the basics!

Working with remainders

What happens when you wind up with a little extra left over, you might ask? While it can look pretty scary, it’s simple to solve.

To do this, you’ll repeat steps one through five above until you get a number that cannot continue to be divided evenly. At this point, you’ll do a few additional steps:

Determine how many times the divisor goes in to the product of your current answer and the divisor. This won’t be a clean number, and that’s OKAY — that’s what your remainder process is for.
Complete the subtraction steps. After you get your number, complete the subtraction steps and write your answer below the subtraction bar.
Do a quick check. If you cannot use your divisor to break your difference down into smaller pieces, that is your remainder. You can note it as: Answer R#.
- For example: In the case of 16 ➗ 3, we would write the quotient as: 5R1.

When you see that there’s zero left over, or if there is no way for the divisor to divide into the dividend, that means that your problem is solved!

Let’s practice some division questions together

1. 20 ➗ 6

We know that our divisor is going to be 6, and our dividend (the number being divided) is 20. We identify them, and we put them into a division bar, like this:
- 6 ⟌ 20
We ask: “How many times can 6 go into 2?”
6 is greater than 2, so we will not be able to put a number over the 2. We then consider, “How many times can 6 go into 20?”
Well, this is a bit of a challenge! 6 does not go into 20 evenly. 6 x 3= 18, and 6 x 4= 24. So, 6 can go into 20 three times, but it won’t go evenly.
So, we add the 3 over the 0, above the division bar.
We put the product of 6 x 3 (our divisor x our quotient) under the dividend and subtract to determine if the a remainder in our difference.
There is a remainder of 2. We write our quotient as: 3R2.

2. 5 ➗ 1

We know that our divisor is going to be 1, and our dividend (the number being divided) is 5. We identify them, and we put them properly into a division bar.
We ask: “How many times can 1 go into 5?”
Instead of working the problem counting or using multiplication, we remember the Division By 1 Property.
We put 5 at the top of our division bar, since any integer that is divided by 1 will always be itself.
There is no remainder for these types of Division By 1 Property problems. We can move on to the next problem.

3. 0 ➗ 2

We know that our divisor is going to be 2, and our dividend (the number being divided) is 0. We identify them, and we put them properly into a division bar.
We ask, “How many times can 2 go into 0?”
Instead of working the problem counting or using multiplication, we remember the Division Of 0 By (Any) Number Property.
We put 0 at the top of our division bar, since any integer that attempts to divide 0 as a dividend will always result in a quotient of zero.
There is no remainder for these types of Division Of 0 By (Any) Number Property problems. We move on to the next problem.

Ready to give it a go?

You’ve done great so far — and you’re well on your way to mastering the art of division. Don’t be afraid to keep trying and make mistakes.

Practice makes perfect, so we’ve given you a few more problems to practice as you work to perfect your skills. Remember: you can always scroll up to walk through the tutorials and refresh yourself on the terms, placement and properties you’ll need to solve these correctly.

By the end of this session, we’re confident that you’ll be ready to claim that A+ on your next maths test. You can do it!

Division practice questions

Question 1: what is 4 ÷ 2?

Question 2: what is 14 ÷ 8?

Question 3: what is 20 ÷ 5?

Answers

The answer is 2.

How did we get here?

We identify 4 as the dividend and 2 as the divisor, and place them in the division bar.
We ask: “How many times can 2 go into 4?” We determine this using the “count by twos” method, which shows us that 2 goes into 4 a total of two times.
We put 2 at the top of our division bar as the quotient, and multiply it by our divisor (2). We then subtract the product of our multiplication from the number to get an answer of 0, which shows us that there is no remainder. You’re done!

The answer is 1R6.

How did we get here?

We identify 8 as our divisor and 14 as our dividend, and place them in the division bar.
We ask: “How many times can 8 go into 14?”, as 8 will not go into 1. We determine this using the “count by eights” method, which shows us that 8 goes into 14 just once.
We write a 1 in the quotient place above the 4 under the division bar. We then multiply 1 x 8 to get a product of 8, which is placed below the 14 under the division bar.
Now, we do the math and subtract 8 from 14. We’ll get 6 as our difference.
We then write our quotient as 1R6.

The answer is 4.

How did we get here?

We identify 5 as our divisor and 20 as our dividend, and place them in the division bar.
We ask: “How many times can 5 go into 20,” as 5 will not go into 2 at all. We determine this using the “count by fives” method, which shows us that 5 can go into 20 cleanly four times.
We place a “4” in our quotient place, and multiply 4 x 5 to get a product of 20. This is written under the division bar as a subtraction problem.
We subtract 20 – 20, resulting in a difference of 0.
This means that 4 is our final quotient with no remainder.

Turn math into an adventure when you sign up for DoodleMaths.

Click here to get started for free!

FAQs about division

What is division?

Division is the mathematical process that breaks down a big value into smaller values.

When will I use division?

There are plenty of times you’ll use division in your everyday life. Some of the most common ways might be to break up an even quantity of something, determining how much of an ingredient to use or grouping up items for use.

What is division the inverse of?

Division is the inverse of multiplication. This means that it naturally undoes any sort of operation that’s done with multiplication.

What are the three main parts of division?

The three main parts of division are the divisor, dividend and quotient.

Try DoodleMaths for free!

Rational vs irrational numbers

Learn about the differences between rational and irrational numbers

Read now

What are odd and even numbers?

We explore examples of odd and even numbers from 1 to 100

Read now

Roman numerals from 1 to 100

Learn the Roman numerals from 1 to 100 and have a go at some questions!

Read now

Lesson credits

What is division in maths?

What is division in maths?

What is division in maths?

What is division?