Maths doesn’t just exist in the classroom–it’s all around us! Go outside and learn all about maths in nature with four free printable maths scavenger hunts. The perfect at-home maths activity for kids.

Jump to any maths activity:
Learn all about maths in nature through photographs and interactive maths scavenger hunts! Our four printable maths activities can be done alone or with light supervision.
Jump to any of the activities below:
Table of contents
It’s easy when you’re sitting in class to think that maths is just something you study in school. But there’s a lot more to maths than adding, subtracting, and solving word problems.
Look around and you’ll see plenty of examples of maths in nature, from fun geometric shapes called fractals to the Fibonacci sequence and more.
Let’s explore where you can find maths in nature this summer (and beyond) — then get outside to see maths in the wild!
Take a look around, and you’ll find that many of the shapes you discuss in class occur naturally in nature, too. In fact, many famous philosophers like Pythagoros probably saw certain patterns in nature and began to ponder why this pattern existed and whether it could be copied—or even just understood—by humankind!
Let’s explore the various shapes we see in nature and what maths can teach us about them.
Circles are one of the most common shapes in nature. From eyeballs to water droplets to the center of a sunflower, you can see circles almost everywhere you go.
This makes sense, because many people believe that the circle is “the perfect shape.” That’s because most humans are attracted to curved lines. In fact, scientists say that most of us find circles calming, peaceful, and relaxing.
One of the most popular – and fascinating – examples of naturally occurring circles are tree rings. Not only do tree rings tell us how old a tree is, but they can also explain what the weather was like in a year, giving us insight into climate patterns.
Use the summertime to take a walk through the woods. You’re likely to find tree ring patterns on stumps or toppled trees. Next time you find one, try to count all the rings to see how old that tree was.

Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Give this a try...
Can you think of all the circles you notice in one day? What about the circles you might not notice until you start looking for them? See how many circles you can find on a nature walk!
You probably wouldn’t think that a hexagon, with its six sides, would be a popular shape in nature, but it’s one of the most common shapes to find in the wild.
In fact, it makes sense, as hexagons are shapes that, when connected, leave the least amount of wasted space in any particular area.
But you’re probably trying to think of places where you’ve seen hexagons and struggling to come up with examples.
You’ll see plenty of bees around in the summertime, right? Well, bees are insects, and almost all insect eyes are made up of hexagonal patterns. However, beehives and honeycomb also contain hexagonal shapes.
Winter might be a few months away, but keep in mind that snowflakes are hexagons, too! All snowflakes begin as small, hexagonal plates. As they fall, they collect crystals that give them their unique shape—but look at the center of any snowflake, and you’ll see a hexagon!
It’s easy to see triangles in many of the buildings and sidewalks you see every day, but did you know that there are plenty of triangles that occur out in the wild?
Take geese migration, for example. Geese fly in a v formation whenever they are migrating from North to South and vice versa. In this formation, the lead bird acts as a windbreak, helping to conserve the energy of the birds behind it by reducing wind resistance.
Each goose in the flock takes turns as the head of the V.

Each bird also flies slightly above the bird in front of them, which also helps to reduce wind resistance and maintains the birds’ energy levels.
Whenever one bird gets tired, it falls back, and the next bird takes its place. This migration pattern uses angles—and specifically, the triangle shape—to help these geese get to where they need to go!
The Fibonacci sequence, also known as the Golden Ratio, goes a little something like this: 1, 1, 2, 3, 5, 8, 13, 21. Basically, add the number to the number that comes before it to get the next number in the sequence, so…
1+1 = 2
2+1 = 3
3+2 = 5
And on and on forever.

Interestingly, this pattern is incredibly popular in nature. You can find the Fibonnaci sequence in flower petals, the seed heads of sunflowers and daisies, and in pinecones. You can also find the Fibonacci sequence in conches and seashells.
What do all of these shapes have in common? They form spirals. And they aren’t the only examples of naturally occurring spirals that follow the Fibonnaci sequence. Peer through a powerful telescope, and you’ll see spiral galaxies. Look at a picture of a hurricane, and you’ll find it there, too.
Have you ever looked through a kaleidoscope and seen a ton of different shapes spinning within other shapes? Well, think of a fractal as just that: shapes within shapes within shapes.
A fractal is a repeating detail or pattern that gets smaller and smaller as it goes, creating gorgeous images that at times seem absolutely unreal.
You might see these when you look at heads of cauliflower, or when you look at the crystals on those snowflakes we mentioned earlier!

The next time you’re out on a summertime walk, take a look around you. You can find curious shapes and symmetry almost everywhere, from pine cones and maple leaves to a head of broccoli. And once you understand that the world is made of math, it might just make you appreciate your math lessons that much more!
Try DoodleMaths for free!
Select a year group
Something is symmetrical when it is the same on both sides, right? Well, we see plenty of examples of this out in nature! Let’s take a look at the monarch butterfly.

Look at each of the features on the butterfly’s wings below. See how they are identical on each side? A butterfly’s wings are (usually) perfectly symmetrical.
This is true of many of nature’s creatures: split them straight down the middle, and aside from a few lumps and bumps, they would likely be symmetrical.
Now that we have unpacked where we see maths in nature, browse our maths in nature scavenger hunts that help you identify shapes and symmetry in nature.
Want some practice before you take to the woods? Download our activity “Tree Ring Circus” and discover how old these trees are!

Let’s explore natural triangles. Download our activity “Fill in the flying v” and turn a flock of geese into colorful triangles.

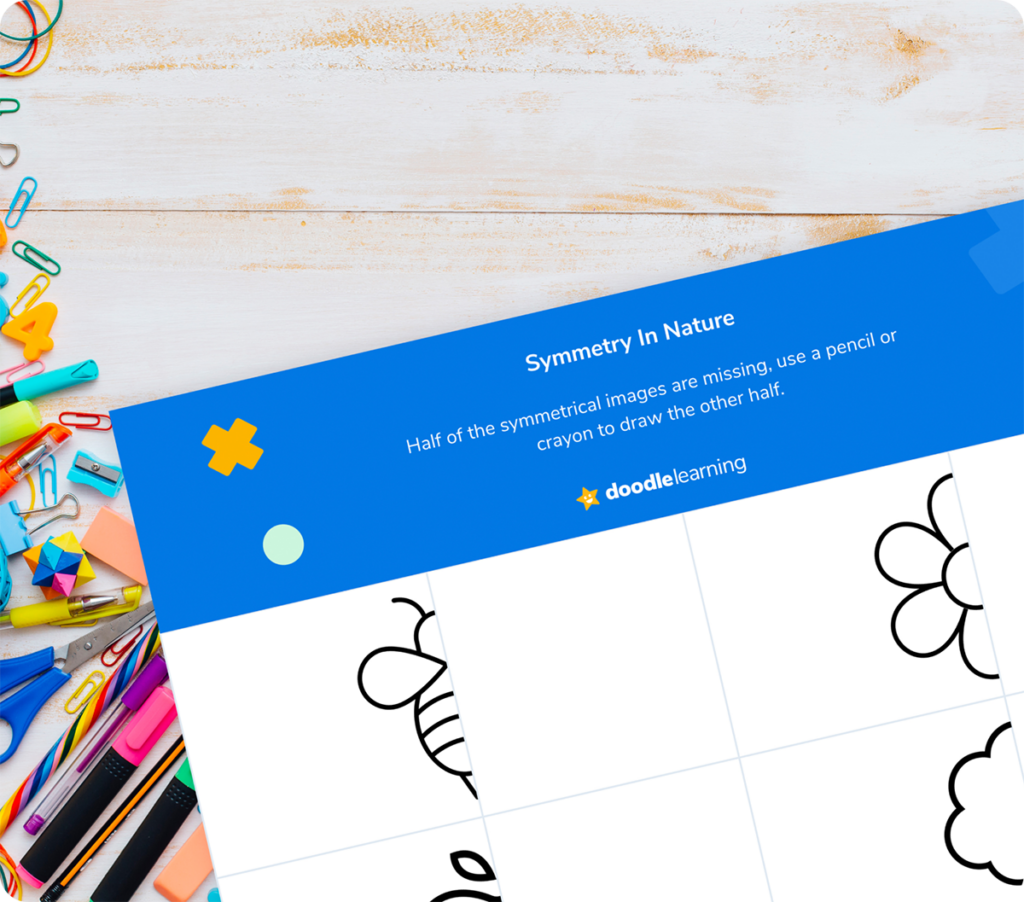
Practice creating symmetry on your own by completing the other side of the animal in the picture. Remember: ‘symmetrical’ means the same on both sides, down to the last spot!
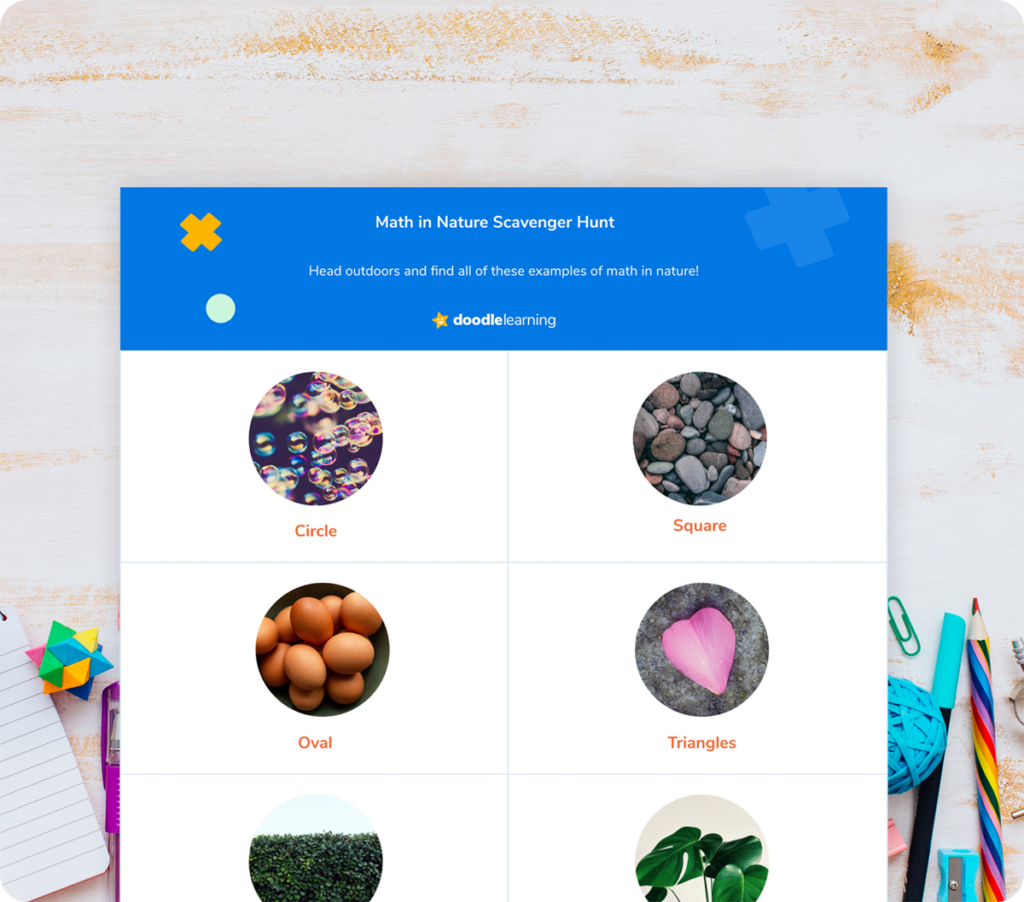
Ready to put your lessons about math in nature all together? Print out the scavenger hunt and take to the woods to find as many summertime shapes as you can!

Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: