Don’t be ‘obtuse’ – learn about the types of triangles and get the answers ‘right’ every time.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: May 2024


Don’t be ‘obtuse’ – learn about the types of triangles and get the answers ‘right’ every time.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: May 2024




Don’t be ‘obtuse’ – learn about the types of triangles and get the answers ‘right’ every time.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: May 2024


Key takeaways
Okay, we know we say every shape is important — and that is true! But if you’re looking for a shape that means serious business, look no further than the triangle.
Not only are there a number of different types of triangles, but calculating a triangle’s area and angles is a crucial part of solving many complex maths problems in later mathematical subjects like precalculus and geometry.
Today, let’s take a closer look at what a triangle is, what properties define a triangle, and the different types of triangles you might encounter in primary school!
A triangle is a two-dimensional shape with three sides, three angles, and three vertices (the points where the sides connect). Because it has three or more sides, a triangle is also considered a polygon, so it belongs in the same shape family as the square, the rectangle, and even the decagon (which has ten sides!).
Interestingly enough, there are not a lot of naturally occurring triangles out there. However, architects and contractors use triangles all the time when they’re building structures to help bear the load and make fantastic designs.
You might also notice that a Give Way sign is shaped like a triangle. So is a clothes hanger and a billiards rack.

A triangle has several different parts. Let’s examine them together.
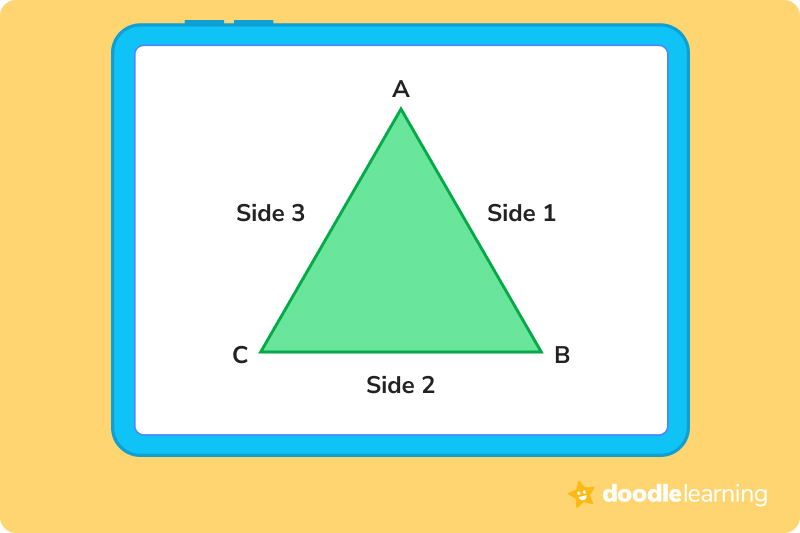
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
There are a lot of different types of triangles. You can categorise a triangle using either its interior angles or the length of its sides – or both, in an ideal world!
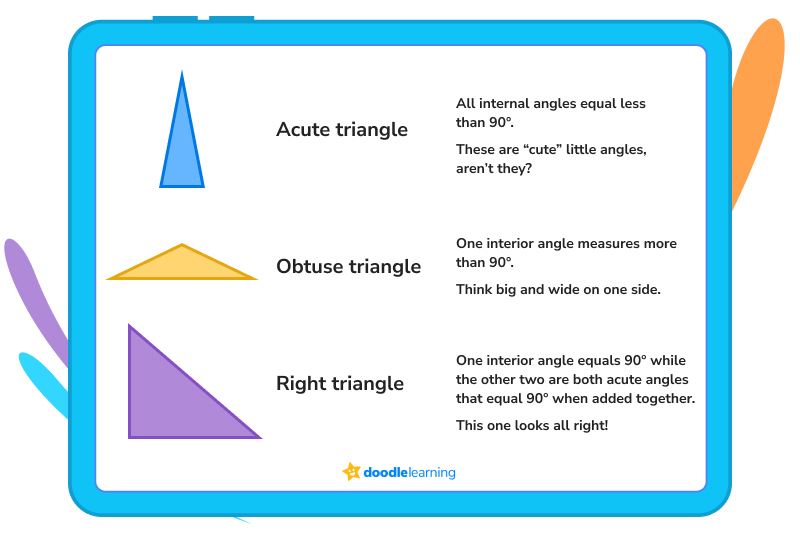
Let’s look at how to categorise using angles first.
There are three types of triangles named for the measure of their angles:
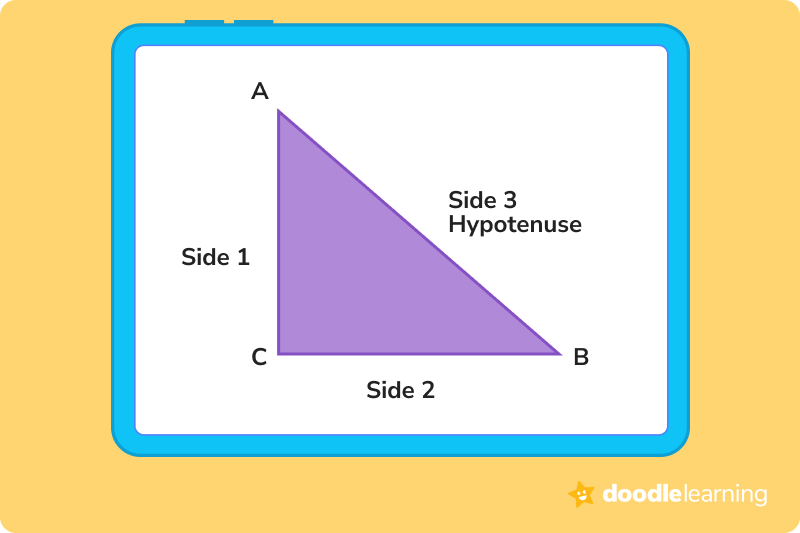
A right triangle has all the same parts as the isosceles triangle. However, there’s a fancy word for the name of the right triangle’s longest side: the hypotenuse.
In a right triangle, the base angle will always equal 90°. The other two angles will always equal 45° each, totaling 90° when added together.
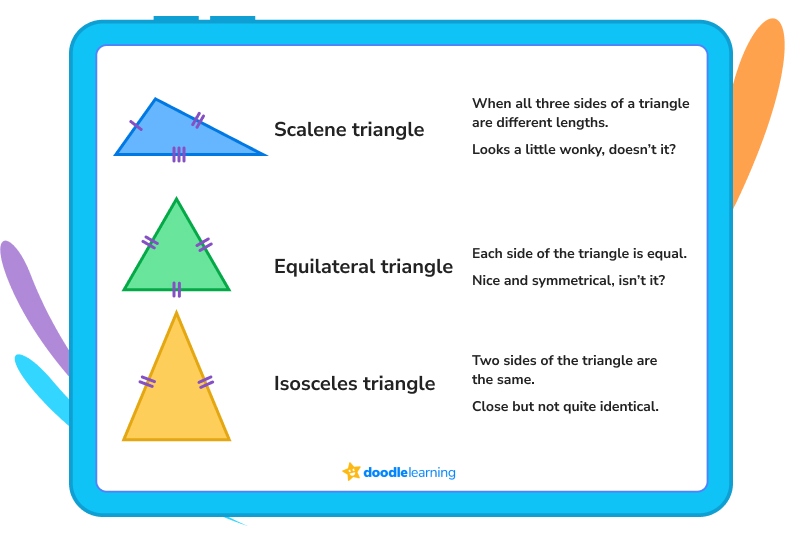
There are also three types of triangles based on the length of their sides:
Look at the hashes on each of the sides of the triangle. They tell you whether the measurements are all equal to each other or different.
Of course, you can combine the two and have triangles labeled for both the length of their sides and their angles.
So, if you have a triangle with equal sides and all angles measure less than 90°, you have an acute equilateral triangle. If you have a triangle with one angle measuring more than 90° and two of three equal sides, you have an obtuse isosceles triangle, and so on and so forth.
Try DoodleMaths for free!
Select a year group
There are a few properties (think of them as rules) that a shape must have in order to be considered a triangle.
We can measure both the perimeter and the area of a triangle. To calculate the perimeter of a triangle, simply add up the lengths of each of its sides.
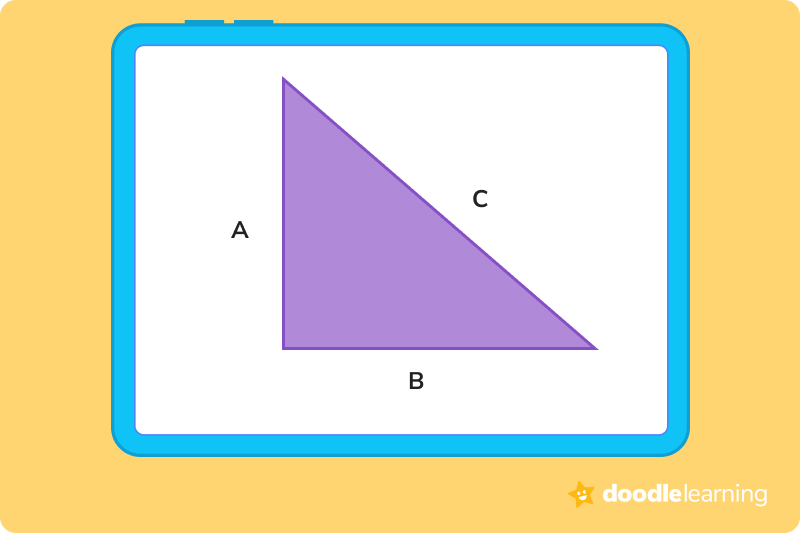
So, if we are looking at a basic triangle with vertices labeled A, B, and C:
P = AB + AC + BC
But calculating the area of a triangle is a bit more complicated—and much more important when it comes to complex mathematics. Let’s learn together!
To determine the area of a triangle, we will need two basic measurements: the length of the triangle’s base and its height.
Now, you might think that you need to just measure the bottom of the triangle to find its base and one of its sides to find its height, but that isn’t true. Let’s break down finding a triangle’s area step-by step.
1. Identify the height of a triangle
Look at the triangle in the example below. The base is BC, so that’s easy to find. However, we don’t know the height yet. How do we find the height?
Split BC in half using figure D. Then, connect D to the triangle’s top vertex, A. Sometimes, the height will be drawn for you, like it is in the figure below. Sometimes, you will have to use your knowledge of right triangles and the formula for area (the Pythagorean theorem) to find the height.
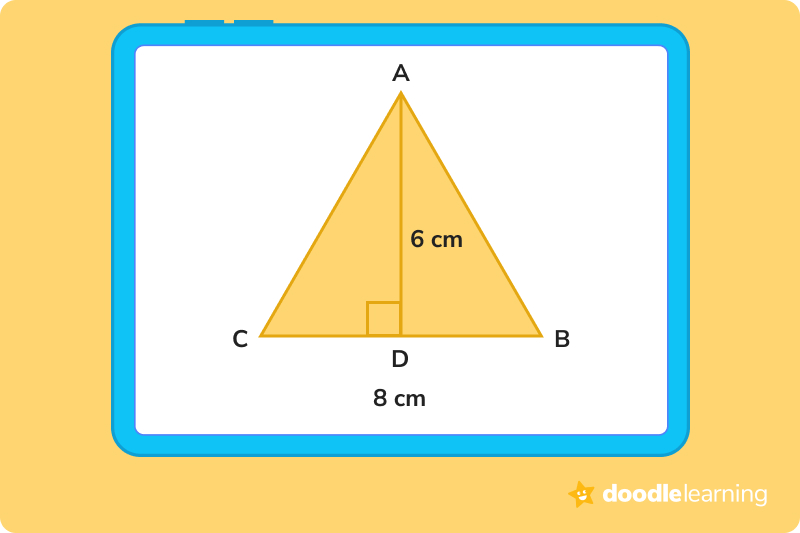
2. Use the formula A = ½ (base × height)
To calculate the area of a triangle, multiply the base and the height together, then divide by 2. In the example above, 8 × 6 = 48, so the area is 48 ÷ 2 = 24.
Practise geometry with DoodleMaths!
Want to learn more about triangles? DoodleMaths is an award-winning maths app that’s proven to double a child’s rate of progression with just 10 minutes of use a day!
Filled with fun, interactive questions aligned to the national curriculum, Doodle creates a unique work programme tailored to each child’s needs, boosting their confidence and skills in maths. Try it free today!


Now that we’ve had a chance to explore the types of triangles and how to calculate perimeter and area, let’s walk through a few practice problems together.
1. Which of the following is a right triangle?
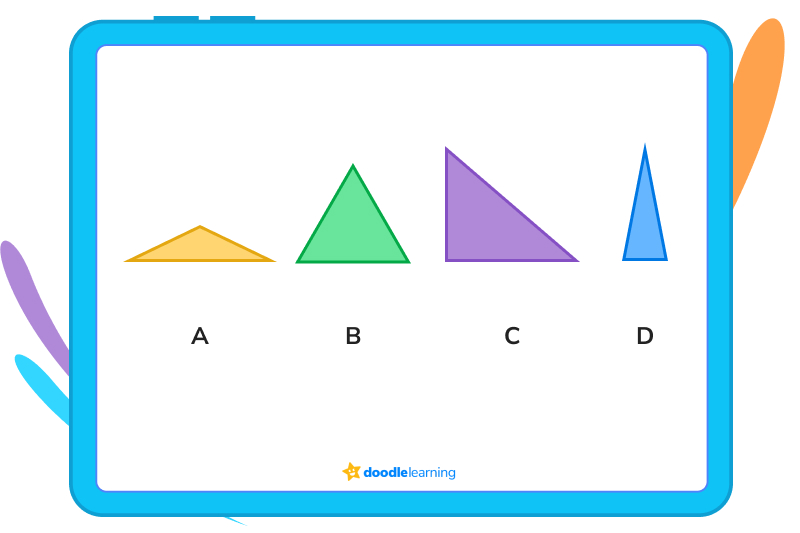
We know that right triangles have to have one right angle, one that measures 90°. The only triangle above that does that is C.
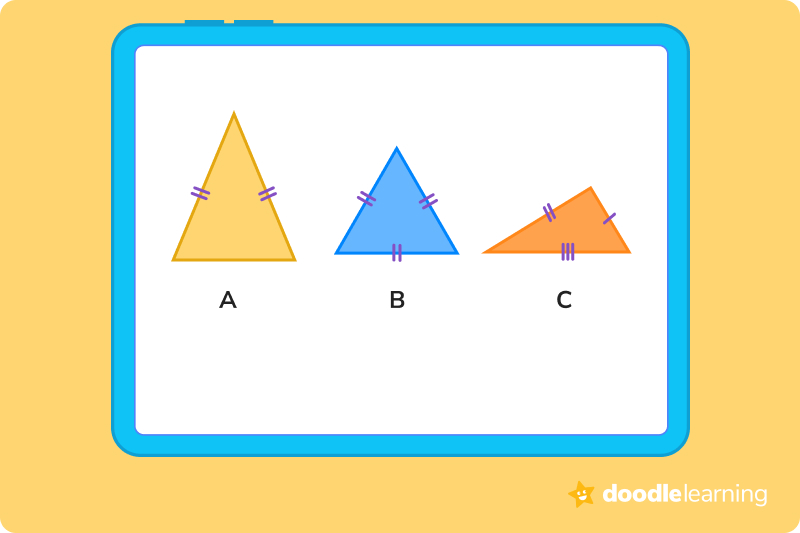
2. Which of the following is an isosceles triangle?
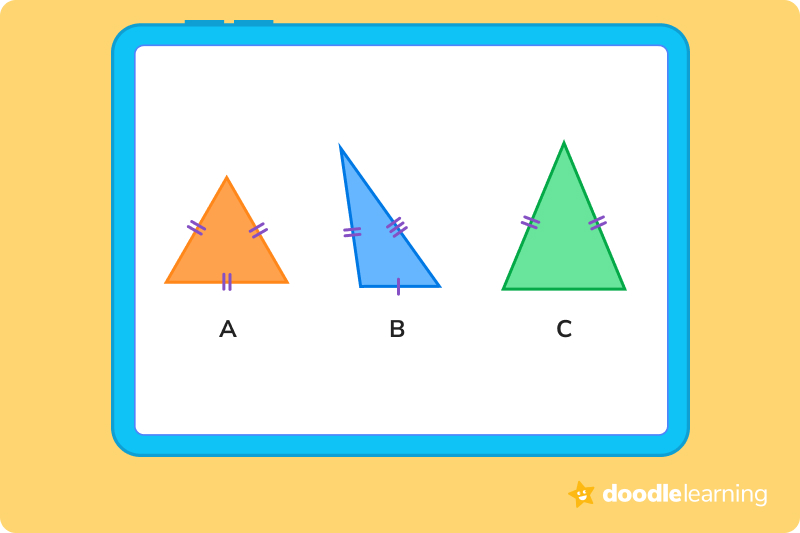
Since an isosceles triangle is equal on two of its three sides, the correct answer is A.
3. Find the area of a triangle with a base of 12 cm and a height of 8 cm.
So first, let’s calculate what the base × height is. 12 × 8 = 96.
So if the area is ½ of the base × height, then the triangle’s area is 48 cm.
We’ve walked you through a few problems—now it’s time to practise on your own! Work through these problems and put your knowledge of triangles to the test.
Click to reveal the answer.
The answer is C.
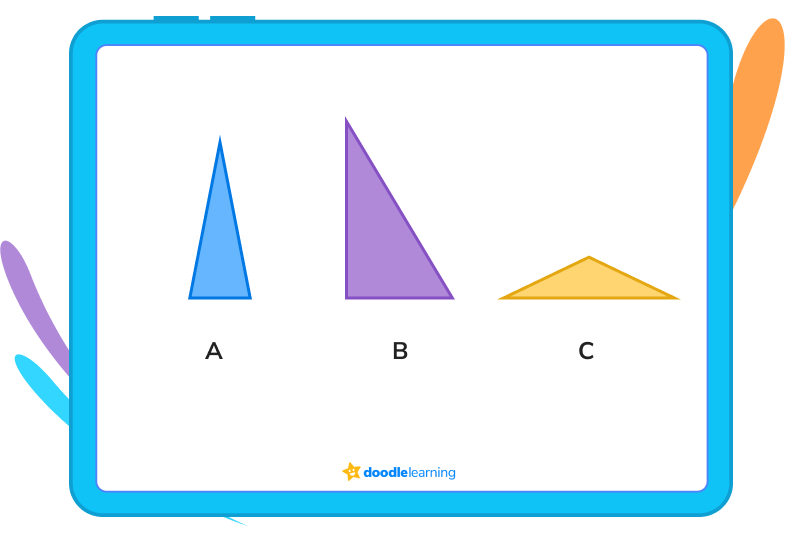
The answer is A.
The answer is C.
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
There are three different triangle types labeled according to the length of their sides.
An equilaterial triangle has 3 equal sides.
An isocoles triangle has 2 equal sides.
A scalene triangle has 3 sides of differing lengths.
There are three different triangle types labeled according to the size of their angles.
In an acute triangle, at least one angle is less than 90°.
In a right triangle, one angle is exactly 90°.
In an obtuse triangle, at least one angle is greater than 90°.
To calculate the area of a triangle, you multiply the triangle’s base by its height, then divide that number by 2.
So if you have a triangle with a base of 16 cm and a height of 14 cm, you get 224 cm. Divide that number by 2, and the area of the triangle is 112 cm.
The Pythagreon theorem is an important equation in geometry. It is also how you find the hypotanuse of a right triangle. The actual equation is written as a2 + b2 = c2, with a being the measure of 1 side and b being the measure of the other side.
So if you had a right triangle with one side that measured 4 cm and another side that measured 8 cm, then to find the hypotanuse, you would calculate:
4 cm2 + 8 cm2 = c2
16 cm + 64 cm = 80
C (or the hypotanuse of the triangle) = √80, or 8.94 if you know your decimals!

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to AP Calculus. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra 1 to AP Calculus. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

The answer is C.
How did we get here?
The answer is A.
How did we get here?
The answer is 36 cm.
How did we get here?
The answer is 18 cm.
How did we get here?
The answer is C.
How did we get here?
The hypotenuse of a right triangle is always its longest side.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: