Let’s learn about one of the most important – and perfect! – shapes in the world.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: May 2024


Let’s learn about one of the most important – and perfect! – shapes in the world.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: May 2024




Let’s learn about one of the most important – and perfect! – shapes in the world.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: May 2024


Key takeaways
Shapes are all around us — from square trucks to the round moon at night, the whole world is filled with shapes. It’s important to understand the principles behind a circle now. You’ll work with circles in class later on, and they are a part of your everyday life.
Let’s learn all about circles!
It might seem pretty simple to identify a circle, but there are a few key features a shape must have in order to be a circle. Essentially, circles around round shapes without any corners or edges.
Circles also have to be closed and two-dimensional. If a shape is a three-dimensional circle, it’s actually called a sphere. If a shape looks like a circle but isn’t complete, like a crescent moon, it might be called a “crescent” shape.
Take a look around, and you’ll find circles practically everywhere! The car you took to school this morning? Its tires are perfect circles. The plate you washed this morning is a circle, too!
Take a look up in the sky, and you’ll see that the Sun is a circle – just be sure not to stare right at it, since it’s the brightest circle around! Sometimes, the moon is a circle. Other times, it’s a crescent or a half-circle.
Let’s take a look at a few more examples:
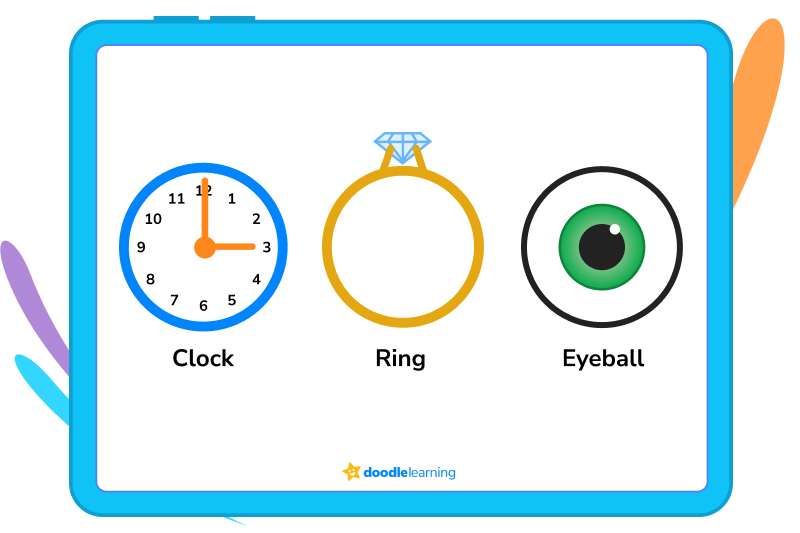
A circle is two-dimensional — you can’t pick a circle up and bounce it across the ground, or use a circle to gaze into the future. But, you can do these things with a sphere!
Basketballs, soccer balls, and other round objects that you can pick up and hold in your hands are spheres. Technically, so is the Sun we mentioned earlier, but from our perspective here on planet Earth, it’s still a circle — like a great, big, shiny coin in the sky.
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
Try DoodleMaths for free!
Select a year group
There’s a lot more to a circle than just its shape. Let’s take a look at all the different parts of a circle.

Let’s take a closer look at some of those invisible lines that run through the interior of a circle and learn how you can use them to find important measurements, like the circle’s area!
The diameter of a circle measures from one side of the circle, through the center, and to the other side.

The radius of a circle is how much space is between the center to the outer edge. You can easily get the radius of the circle by dividing the diameter in half.

Have you ever run around the outside of a track? Then you’ve run its circumference! A circle’s circumference is the distance around the circle. It’s the same as the perimeter of shapes with angles and straight lines.

Chords in a circle are any line segments that go from one side of a circle to the other. As long as both endpoints of the line lay on the outer edge of the circle, then it’s a chord. Yes, the diameter of a circle is also a chord!
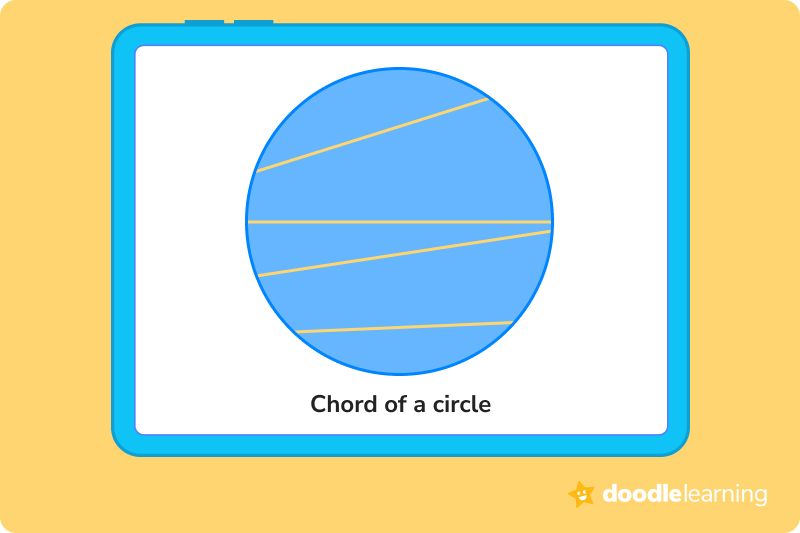
A secant is a straight line that intersects a circle in two places and continues on outside of the circle. Imagine that you lay your pencil down on top of a circular cookie. Your pencil is now a secant!
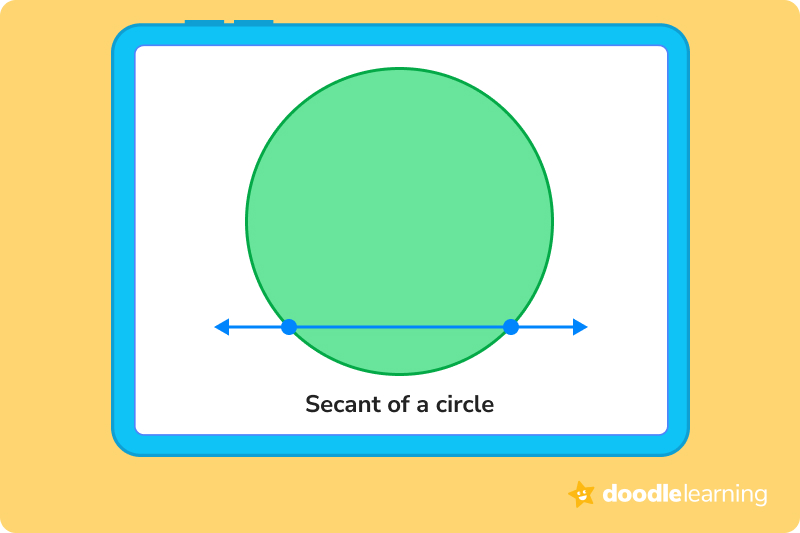
A tangent is a line that’s outside of a circle, but that rests on the edge of the circle. For example, when a basketball is sitting on a shelf or a paved court, the surface it’s resting on is the tangent.
Circles can be split up, too. For example, pizza slices are parts of a circular pizza. However, understanding how to split up a circle may help you cut more equal slices to make sure everyone gets the same amount! That’s one reason why maths is so important: it helps you better understand how to make things truly equal.
Without maths, it’s hard to divide up a circle equally.
Measure the diameter of a circle, cut along the diameter, and you make a semicircle. Put another way, if you cut a circle in half, you produce a semicircle.
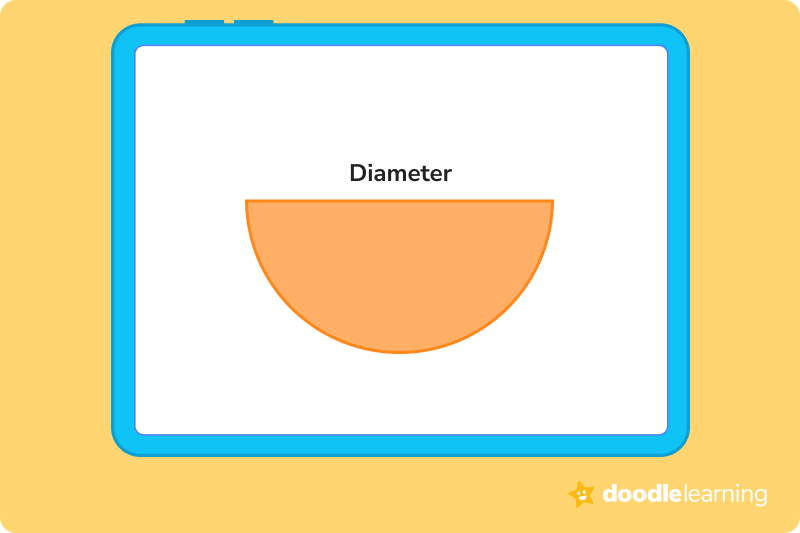

A circle’s area is how much space it takes up. The diameter and the number for pi are all you need to know to find the circle’s area.
Use this formula to find a circle’s area:
A = π x r2
In this formula, A = area, which is what we’re trying to find. Pi, or Π, is a ratio we use for the circumference of circles. Then, we use the radius multiplied by itself to solve for the area.
Pi is equal to 3.14.
Why does it say r2? The little 2 next to the r represent the practice of squaring. Basically, squaring is a quick way to say that whatever r is, you multiply it by itself.
Here’s an example:
The circle below has a radius of 25mm.
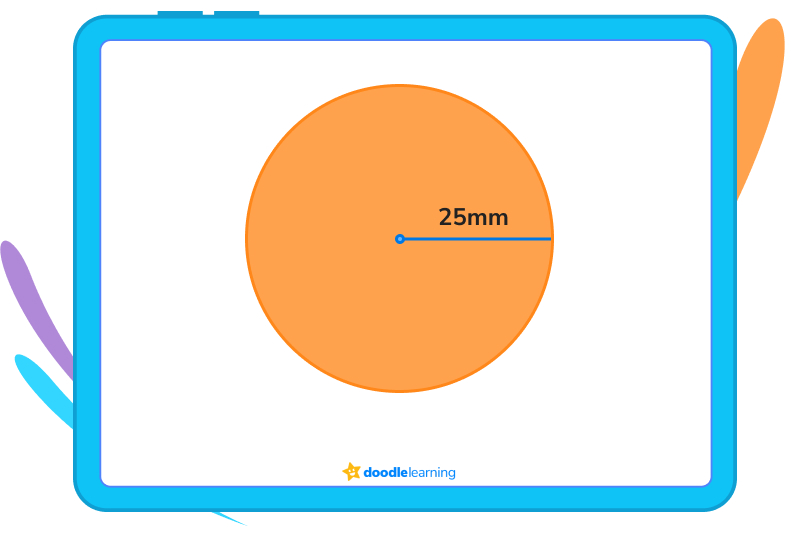
To find the area, we would plug the right numbers into the formula, like this:
A = 3.14 x 252
25 mm x 25 mm = 625 mm
625 mm x 3.14 = 1,963 mm
1,963 mm = 3.14 x 252
Understanding what a circle is and how to find its area is foundational to understanding more advanced mathematics, like geometry and trigonometry. Keep practising to build your confidence and become a circle master!
Want to learn more about circles? DoodleMaths is an award-winning maths app that’s proven to double a child’s rate of progression with just 10 minutes of use a day!
Filled with fun, interactive questions aligned to the national curriculum, Doodle creates a unique work programme tailored to each child’s needs, boosting their confidence and skills in maths. Try it free today!


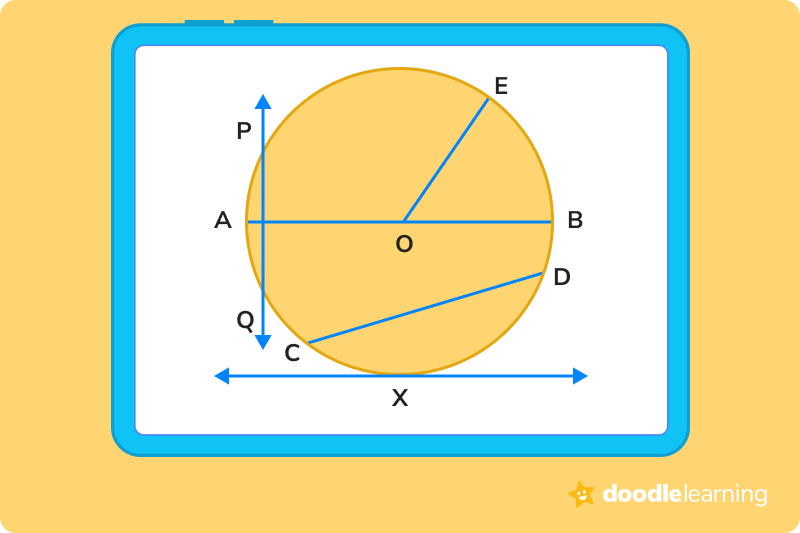
Now that you know the parts of a circle and how to measure them, take a look at the figure and answer the problems below!
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
The diameter of a circle is a straight line segment that passes through the center of the circle and connects two points on the edge (called the circumference) of the circle. It is the longest distance you can measure within a circle.
The size of a circle is typically measured using its radius or diameter. The radius is the distance from the center of the circle to any point on the edge. The diameter is the distance across the circle passing through the center.
We can use these measurements to calculate other important quantities like the circumference (distance around the circle) and the area (the space inside the circle).
Pi (π) is a special mathematical constant that is related to circles. It represents the ratio of the circumference of any circle to its diameter. No matter the size of the circle, this ratio remains the same.
Pi is approximately equal to 3.14159, but it goes on infinitely without repeating any pattern. Pi is important in many mathematical calculations involving circles, such as finding the circumference or the area.


Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
The answer is line O.
How did we get here?
The diameter of a circle is the width of it through the exact center. Students can find this by identifying the line that passes through the center of the circle and touches both outer edges. In our illustration, that’s line O.
The answer is line E.
How did we get here?
The radius is the width from the center of a circle to the outer edge. In our illustration, that’s line E.
The answer is line X.
How did we get here?
The secant line is a line that touches a circle at the same, opposite two points. In our illustration, that’s line C-D. The Tangent only touches the outer edge at one point, and in our illustration, that’s line X.
The answer is 1,809 inches.
How did we get here?
The answer is 1,017 mm.
How did we get here?
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: