No matter which order you put things in, you’ll always get the same answer – at least when it comes to addition!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: January 24, 2024


No matter which order you put things in, you’ll always get the same answer – at least when it comes to addition!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: January 24, 2024




No matter which order you put things in, you’ll always get the same answer – at least when it comes to addition!

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: January 24, 2024


Key takeaways
There are a lot of rules in maths. Sometimes, this can make the subject seem dry or boring, but actually, these rules are meant to help make things a little easier!
Think of the associative property as a rule of addition. To “associate” means to connect or join with something else. In addition, we’re connecting different numbers together to create a sum.
The associative property tells us that no matter how we arrange three or more numbers in an equation, we’ll always get the same sum. But how and why? Let’s take a closer look.
The associative property of addition states that the sum of three or more numbers will always remain the same, regardless of how the numbers are grouped. But what is grouping, and how does it work? Let’s break it down.
Grouping is the practice of bringing two or more terms together into a group.
In an equation, we usually represent grouping by using parentheses.
For example, let’s say we have the equation:
4 + 5 + 6 + 7 = 22
We can use grouping to make this equation a little easier to read. All we have to do is group two terms together. In this case, we could group the first two terms together and the last two terms together.
So now the equation looks like this:
(4 + 5) + (6 + 7) = 22
If we solve the parentheses to simplify the equation, we get:
9 + 13 = 22
Put simply, whenever you add multiple numbers together, you can group them any way that you like and still end up with the same answer. That’s because you still have the same quantity, regardless of how you write the equation.
Let’s take a look at what this means visually:

Even if we switch the order of things, the number of hearts remains the same.
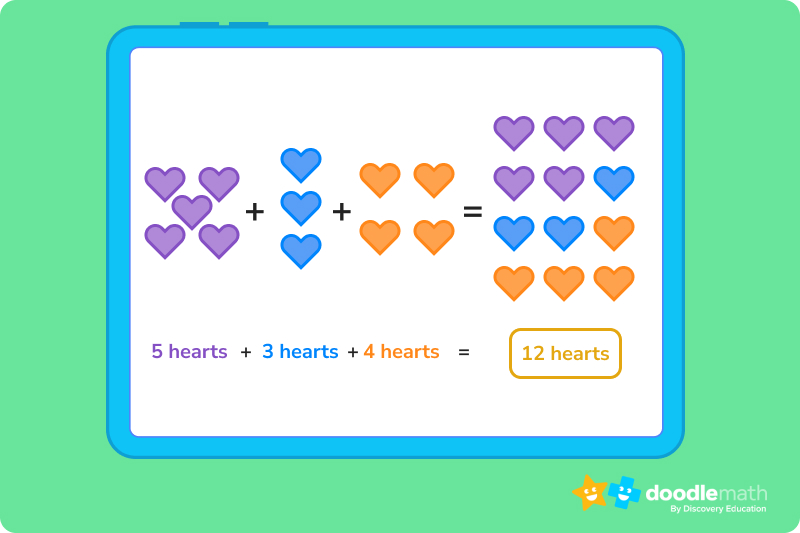
Let’s look at how you can write equations a few different ways and, using the associative property of addition, still get the same result.
Let’s examine this equation:
6 + 8 + 10 + 12 = 36
Now, we’re going to use grouping and see if we can make that 36 number change (spoilers: we can’t!).
First, let’s make it simple and just group the numbers as they’re written.
(6 + 8) + (10 + 12) = 36
We’ll solve the addition problems in the parentheses and get:
14 + 22 = 36
Okay, what if we swap the numbers on the end?
12 + 8 + 10 + 6 = 36
And put them into parentheses?
(12 + 8) + (10 + 6)
We’ll solve the addition problems in the parentheses and guess what?
20 + 16 = 36
And on and on it goes!
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
Think about the word “commute.” It means to move, right? The commutative property of addition says that we can rearrange the order of numbers and still get the same result.
In other words, the commutative property helps make the associative property true.
To put it into an equation:
A + B = B + A
Or, if you decide to rearrange it:
B + A = A + B
Neat, right?!
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!


The associative property also applies to multiplication! So, let’s take a look at a multiplication problem.
Say you have:
4 × 6 × 7 × 4 = 672
If we group those in order, we get:
(4 × 6) × (7 × 4) = 672
4 × 6 = 24
7 × 4 = 28
And that becomes:
24 × 28 = 672
Now, let’s swap some things around:
7 × 6 × 4 × 4 = 672
Grouped, that looks like:
(7×6) × (4×4) = 672
7×6 = 42
4×4 = 16
And that becomes:
42 × 16 = 672
Using the associative property makes finding the sum (or the product!) easier when you have multi-digit numbers to add together. Just keep this rule in mind as you dive into your maths homework, and you can conquer those problems with ease!
1. Find the sum: (5 + 6) + (7 + 8)
So, since these are grouped together, we can break this up into parts to find the sum.
First, we’ll add the numbers in parentheses together:
5 + 6 = 11
7 + 8 = 15
Then, add these larger sums together:
11 + 15 = 26
2. Find the sum: (7 + 5) + (6 + 8)
Instead of going through the long process of solving, look at the answer above. Using the associative property of addition, we know that the sum is 26.
Ready to give it a go?
Now that you’ve learned all about the associative property of addition, it’s your turn to shine! Solve the following problems to test your knowledge and understanding.
Click to reveal the answer.
The answer is 40
The answer is 30
The answer is YES
The answer is 5,184
The answer is 40.
How did we get here?
If you add all of these numbers together, you get 40.
The answer is TRUE.
How did we get here?
Using the associative property, we know that you can group the numbers in a different order and still get the same sum.
The answer is 30.
How did we get here?
The answer is YES.
How did we get here?
Using the associative property of addition, we know that no matter what order the numbers are in, if they are the same numbers, they will produce the same sum.
The answer is 5,184.
How did we get here?
Sign up for the DoodleMaths app today!
Turn math into an adventure when you sign up for DoodleMaths.
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
According to the associative property, while adding or multiplying numbers, the way in which the numbers are grouped by brackets does not affect their sum or product.
You can shuffle the numbers however you like within the equation, but the answer will always remain the same.
The associative property states you can group different numbers in various ways without changing the outcome. The commutative property states you can reorder the numbers without changing the outcome.


Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: