A guide for negative numbers and their real-world applications
Author
Tess Loucka
Published
January 22, 2024
A guide for negative numbers and their real-world applications
Author
Tess Loucka
Published
Jan 22, 2024
A guide for negative numbers and their real-world applications
Author
Tess Loucka
Published
Jan 22, 2024
Key takeaways
Have you ever woken up in the morning to see frost covering your window and snow piled high on the ground outside? Or maybe you’ve peeked into your freezer to see icicles hanging from the ceiling, and ice covering bags of frozen peas.
In these instances, you may have looked at a thermometer wondering just how cold it is. Sometimes it’s so cold the number on the thermometer is less than 0 and the numbers turn into negatives. But what is a negative number anyways?
We see numbers every day when reading the forecast, making purchases, or getting a score on a quiz, and they’re not always positive! In our daily life, and in maths problems, we come across negative numbers all the time.
So, let’s go over what negative numbers are and how they’re used.
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
Negative numbers are any numbers smaller than zero. They are represented with a minus sign (-) followed by a digit, such as -3, -2, -1, etc.
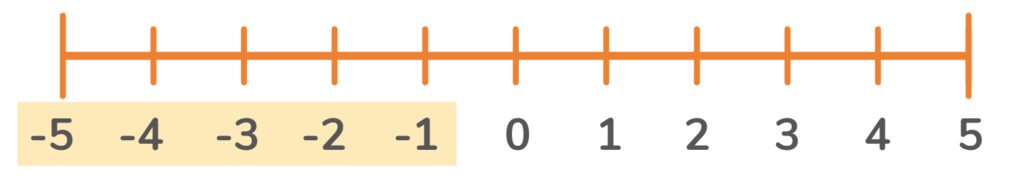
The highlighted side of the number line above is the negative numbers side. They are to the left of the 0 because they have a smaller value than 0. Those to the right of the 0 are positive numbers. They have a greater value than 0.
As stated above, a negative number is any number smaller than zero. However, there are a few more properties of negative numbers that you should know.
Want to learn more about negative numbers? DoodleMaths is an award-winning app that’s filled with thousands of questions exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!
We already mentioned that negative numbers appear on thermometers to show us that the temperature is “below zero”, but that’s not the only real-life example of negative numbers.
Negative numbers are all around us! When we make purchases, the money or credit due is a negative number. Negative numbers also appear on elevation maps to indicate places that are “below sea level”.
Negative numbers can be used as penalties in games, quizzes, and tests. When you get an answer wrong, you may get -5 points, meaning 5 points are being taken away from your total score.
In sports, too, negative numbers can be used to denote the scores of teams. One great example is golf. The golfer with the lowest score, which represents the least amount of strokes, wins!
As you can see, there are many real-world applications of negative numbers. They may not be as common as positive numbers, but they’re just as important.
Now, let’s go over the rules for working with negative numbers.
When working with negative numbers in addition and subtraction problems, there are certain laws that you will find to always be true. Remember these laws to make solving problems with negative numbers in the future easy!
One tip for adding and subtracting negative numbers involves the number signs beside each digit (+ or -):
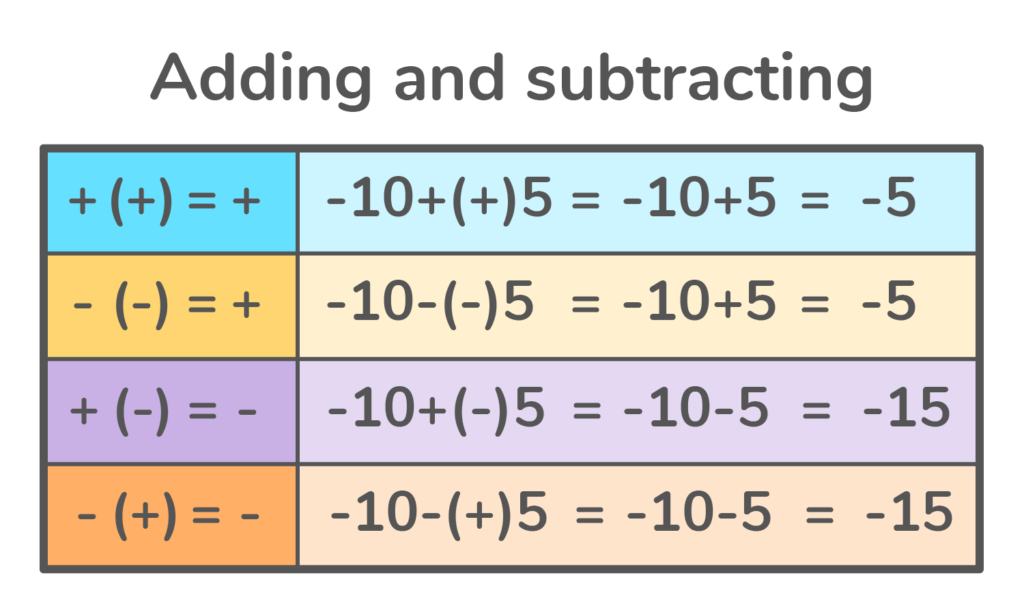
When adding negative numbers, if the signs of the two numbers you are adding are the same, add the numbers together and keep the sign the same.
-6 + -2 = -8
Since + and – are next to each other in this problem, you can replace them with one negative sign (-). So, this problem can also be written as -6 – 2 = -8
If the signs of the two numbers are different, keep the sign of the greater absolute value.
6 + -2 = 4
Again, you can replace the + and – with one – sign. So, this problem can also be written as 6 – 2 = 4.
When subtracting negative numbers, if the signs of the numbers are both negative, switch the two adjacent negative signs to a positive.
-6 – (-2) = -4 can also be written as -6 + 2 = -4
If the signs of the numbers are different, switch the subtraction sign to an addition sign, and switch the sign of the second number.
-6 – 2 = -8 becomes -6 + -2 = -8
-2 – 6 = -8 becomes -2 + -6 = -8
The laws to remember when multiplying and dividing negative numbers are actually more straightforward than those for adding and subtracting them.
All you need to know is that when multiplying or dividing numbers with the same sign, the result will be positive. If the signs are different, the result will be negative.
When multiplying two negative numbers together, the result will be a positive number.
-6 x -2 = 12
When multiplying a positive number with a negative number, the result will be a negative number.
6 x -2 = -12
When dividing two negative numbers together, the result is a positive number.
-6 ÷ -2 = 3
When dividing a positive number and a negative number, the result is a negative number.
6 ÷ -2 = -3
The more examples of negative number equations you go over, the more comfortable you will be with working with negative numbers. A good maths app can provide you with as many examples as you need, as well as detailed solutions and explanations that make learning maths easy and fun.
Check out our step-by-step video to find out how to order negative numbers! Be sure to check out our bank of topic walkthroughs for even more guides (perfect for sharing with your child or in class).
Click on the boxes below to see the answers!
When subtracting negative numbers, remember that two negatives equal a positive. Change the two negative signs into a positive. -10 – (-4) becomes -10 + 4. You can use mental math or a number line to get -6 as your answer.
Multiplying any two numbers with different signs results in a negative number. So, -4 x 5 is -20.
To add two negative numbers, add the digits together and keep the sign the same. So, -9 + -3 becomes -12. You can also rewrite this as -9 – 3.
Yes, negative numbers are real numbers.
Negative round numbers are integers, but any fractions or decimals are not.
No, negative numbers are not whole numbers. Whole numbers are only positive round numbers, including 0.
Most negative numbers are rational numbers. If a number can be written as a fraction, that means it is a rational number.
Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!
Lesson credits
Tess Loucka
Tess Loucka discovered her passion for writing in school and hasn't stopped writing since! Combined with her love of numbers, she became a maths and English tutor. Since graduating, her goal has been to use her writing to spread knowledge and the joy of learning to readers of all ages.
Tess Loucka
Tess Loucka discovered her passion for writing in school and hasn't stopped writing since! Combined with her love of numbers, she became a maths and English tutor. Since graduating, her goal has been to use her writing to spread knowledge and the joy of learning to readers of all ages.
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
