Turn your big numbers into smaller ones with long division – just master these easy steps!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Published: August 24, 2023
Turn your big numbers into smaller ones with long division – just master these easy steps!
Author
Taylor Hartley
Expert Reviewer
Jill Padfield
Published: August 24, 2023
Turn your big numbers into smaller ones with long division – just master these easy steps!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Published: August 24, 2023
Key takeaways
Table of contents
Long division might seem a little complicated, but anything’s easier when you divide it into smaller parts!
Let’s explore the process of long division and why it’s so important. First, we’ll explain what long division is and how it relates directly to another important concept — multiplication. If you’ve already mastered the basics of multiplication down, long division won’t be that bad, we promise!
Finally, we’ll run through a few practice examples to make sure you’ve got the hang of things before you go back to the classroom.
Long division is the process of reducing a multi-digit number into smaller groups.
It’s also the practice of reversing multiplication: taking a certain value and separating it into different numbers that were multiplied together to equal that original value.
Division is an important skill if you want to reduce numbers more efficiently, but long division is especially important as those numbers get bigger and bigger.
Long division is a helpful way of breaking a larger number up into two smaller ones. It follows a sequence of steps that, once mastered, makes the process of reducing any large number much easier.
You’ll encounter long division a lot when practicing mathematics, so it’s important that you get the basics down early. You never know when you might need to use it in your everyday life—and trust us, you will!
Follow along as we learn and practice the basics of long division.
One of the most important parts of understanding division is that it’s the opposite of another common mathematical operation — multiplying.
The same way you think of multiplication as repeatedly adding a certain value over and over again, division is the practice of subtracting a certain value over and over again, with the number of times you subtract being the quotient.
Think of multiplication as the repeated addition of equal values. And think of division as a way of finding out what those equal values are, and how many times you’re adding them. This way, you’ll be able to see how multiplication and division are inverses, or opposites, of one another.
Before we get into the basic steps of how to perform long division, we need to define a few important terms so that we can better understand these steps. There are four main definitions involved in the process of long division:
Get 2 FREE weeks of Doodle!
Use code 2WKS_AUTUMN to enjoy unlimited questions and games
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Try DoodleMaths for free!
Select a year group
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Let’s take a look at a practice problem. This is a good opportunity to rinse and repeat the basic steps of long division, and make sure you’ve got the main points down before we go on to some other practice examples. Take a look below:
Solve 225÷5
Make sure the divisor is written first, and separate it from the dividend by either a right parentheses [)] or a backslash [/].
Then, draw an overhead bar above the dividend that connects to the parentheses or backslash you just drew. This will help you understand the difference between divisor and dividend.
Now, let’s take a look at the first number from the left in our divisor. Since 2 is less than 5, the dividend, we know we can’t do any division here. So, we write a 0 as our first number in the quotient and multiply it by our 5, giving us a product of 0.
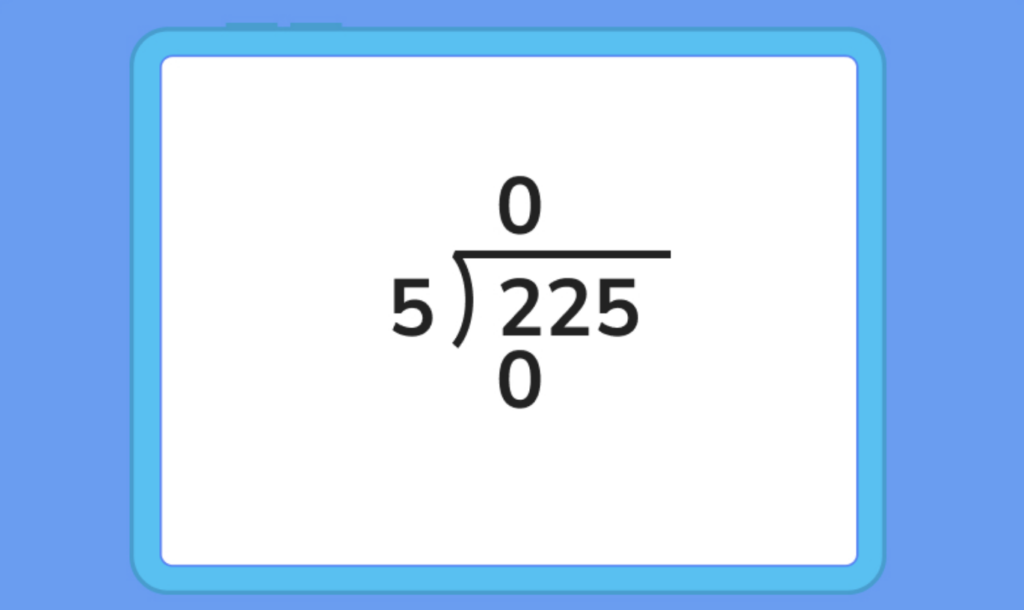
We then need to subtract this 0 from the first digit of the dividend, 2. Now we can drag the 2 in the tens place down and place it next to the difference we calculated in step 2. This gives us a value of 22.
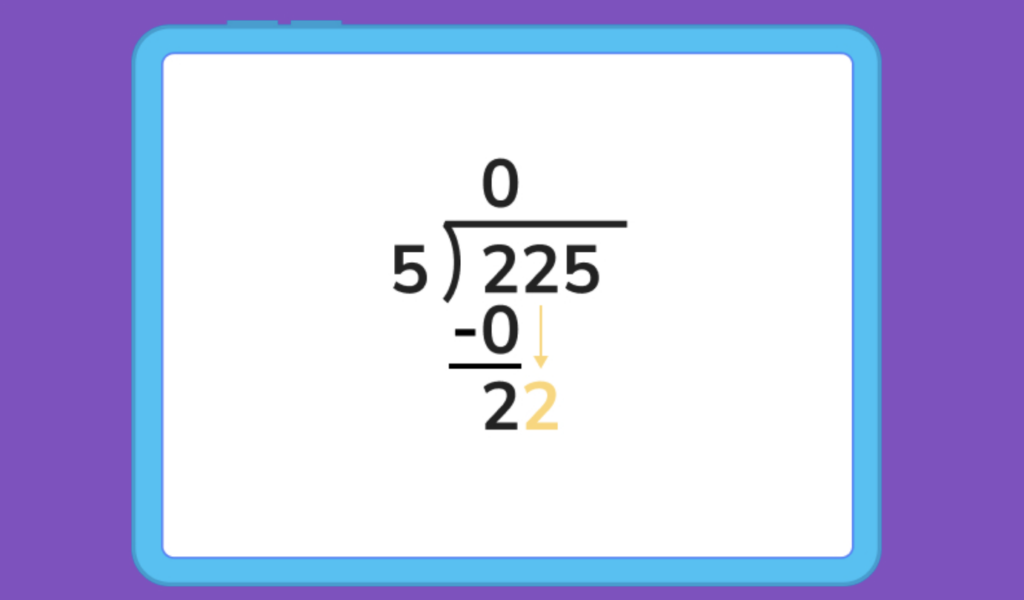
22 isn’t divisible by 5, but we know 5 x 4 = 20, or that 5 fits into 20 four times. That means we can write a four in the quotient to the right of our 0. We then write that 20 below our 22, and subtract.
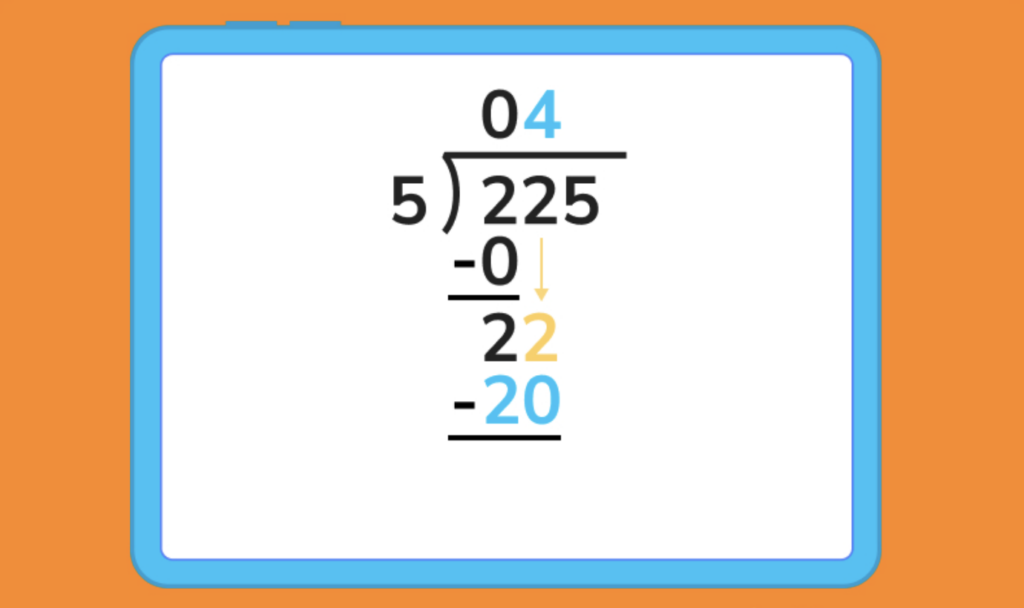
Our subtraction from step 4 gives us a value of 2. Now we drag the 5 in the ones place of 225 all the way down next to that 2, giving us a value of 25.
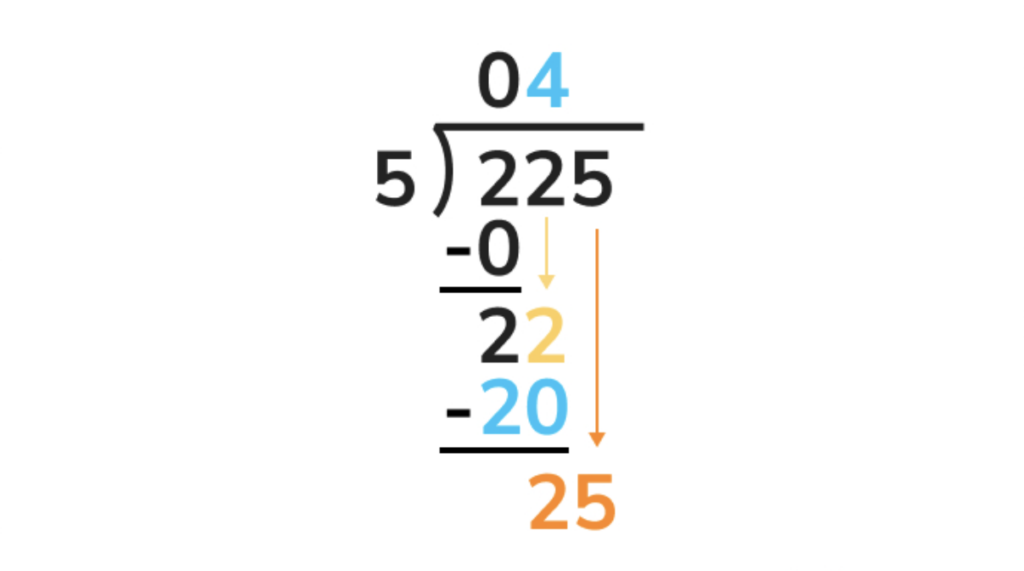
Now, we can divide that final 25 by our original dividend of five. 25 divided by 5 equals 5, which we write in the final place of our quotient.
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!
Solve 135 ÷ 6
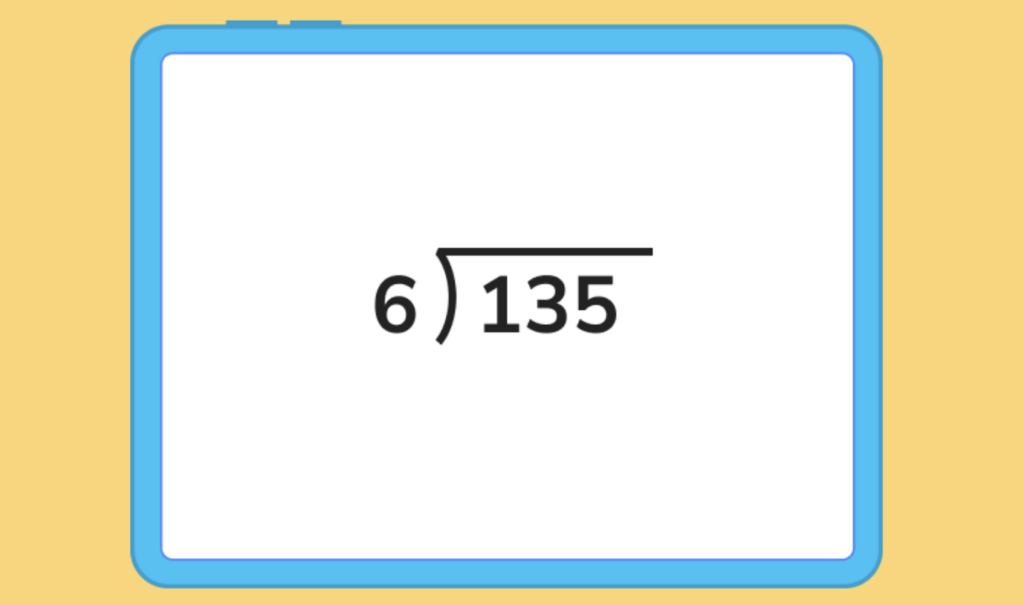
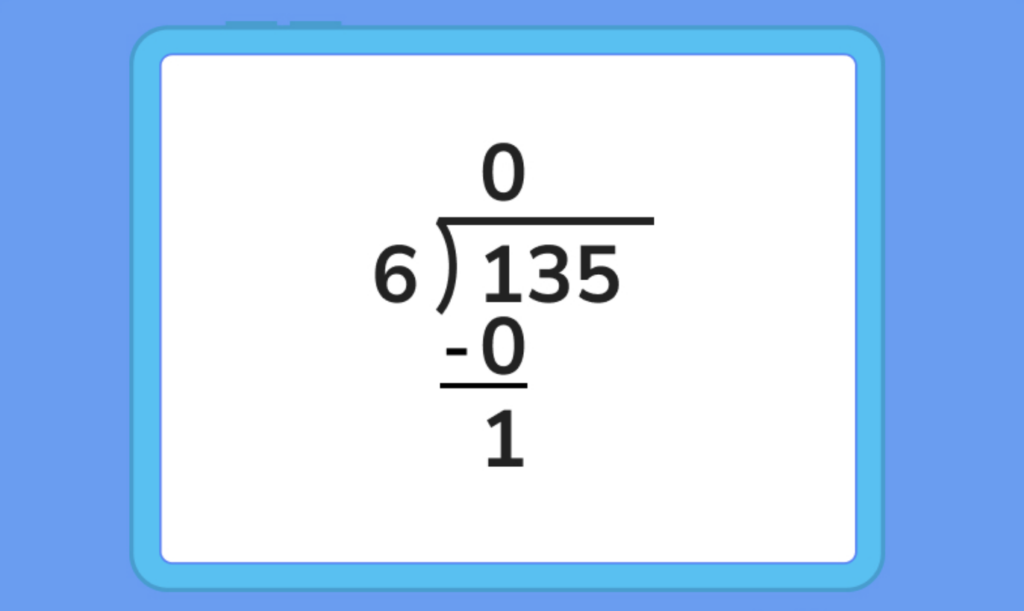
1. Since we know 1 is less than 6, we can write a 0 as the first number in our quotient, and drag our 1 down.
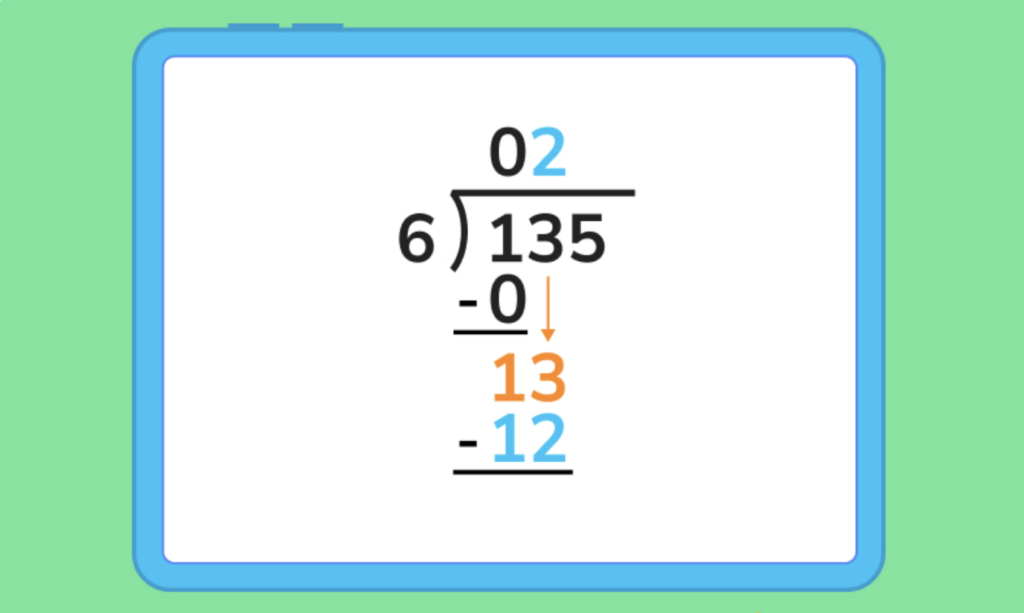
2. We then drag the 3 down next to our 1, giving us a value of 13. Since 6 fits into 13 twice, 6 x 2 = 12, we can write that 2 next to our 0 in the quotient.
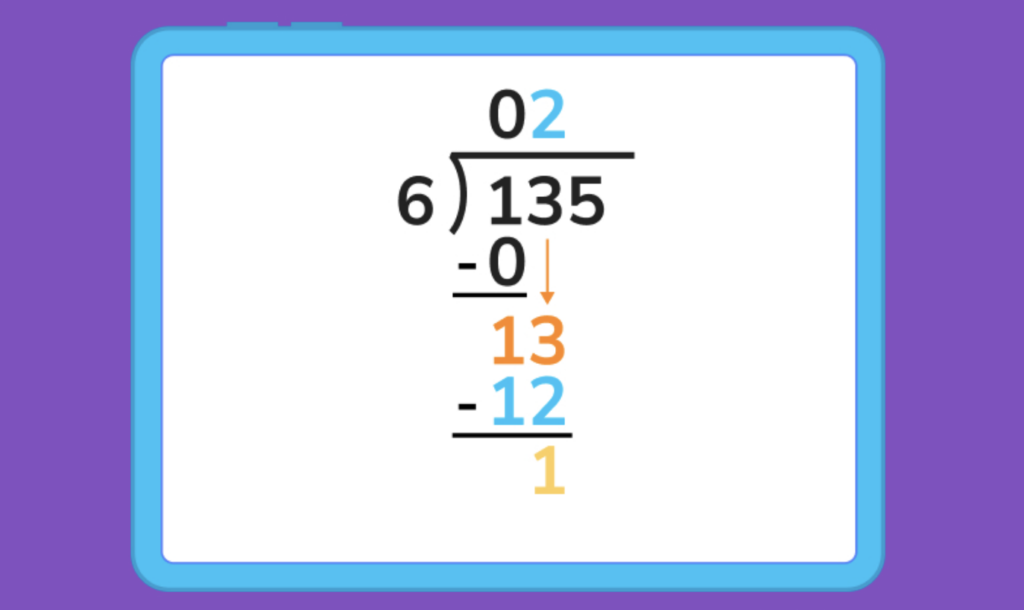
3. We then subtract 12 from 13, giving us a 1.
4. Now we can drag our 5 down and place it next to that one, giving us 15. Six fits into 15 twice, meaning we can write another two in our quotient.
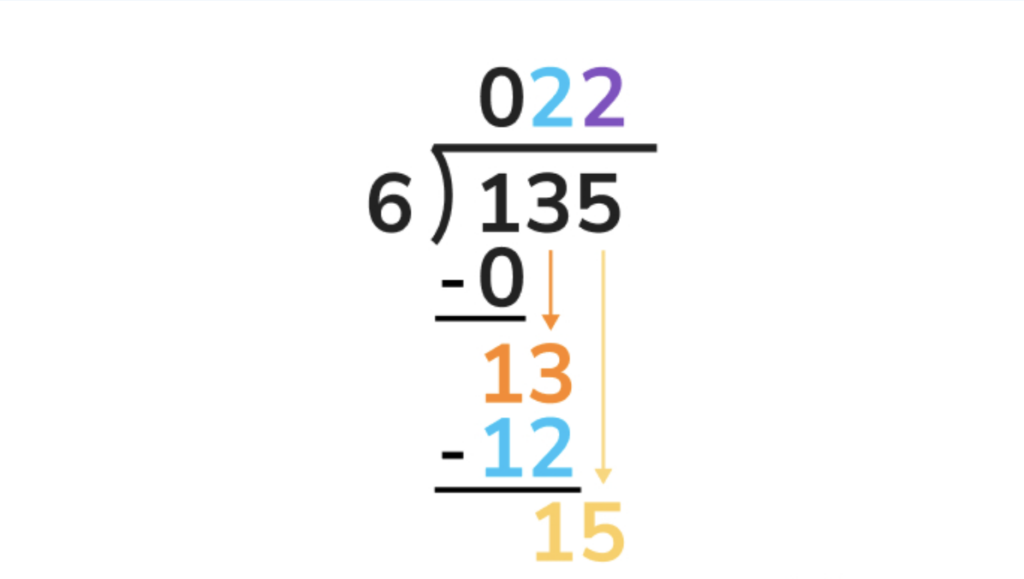
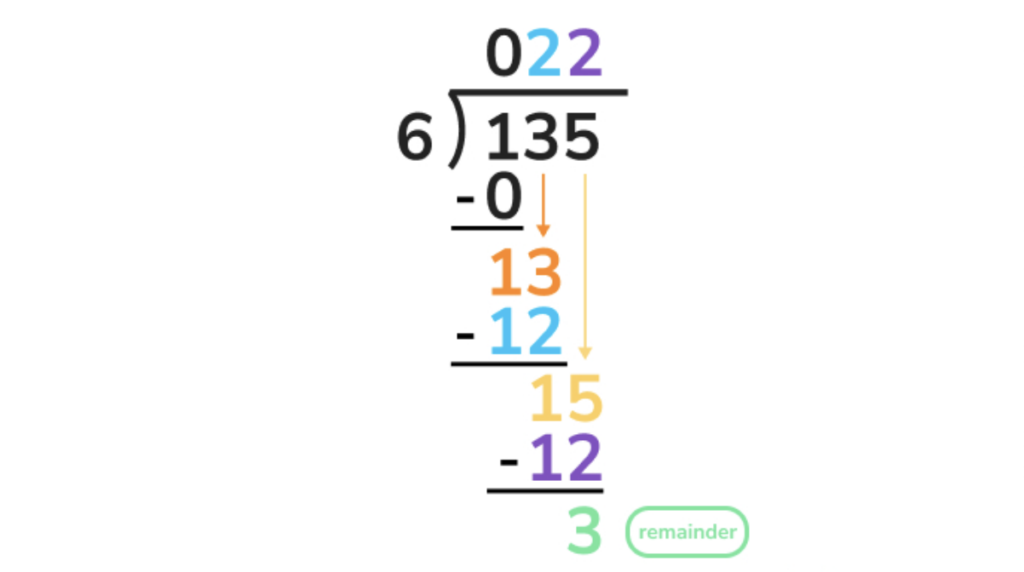
5. However, 15 – 12 = 3, and there are no more numbers to drag down! Here is where we use the term REMAINDER. 3 is the remainder here, since there is no more possible division to perform. Our final answer is 22 with a remainder of 3.
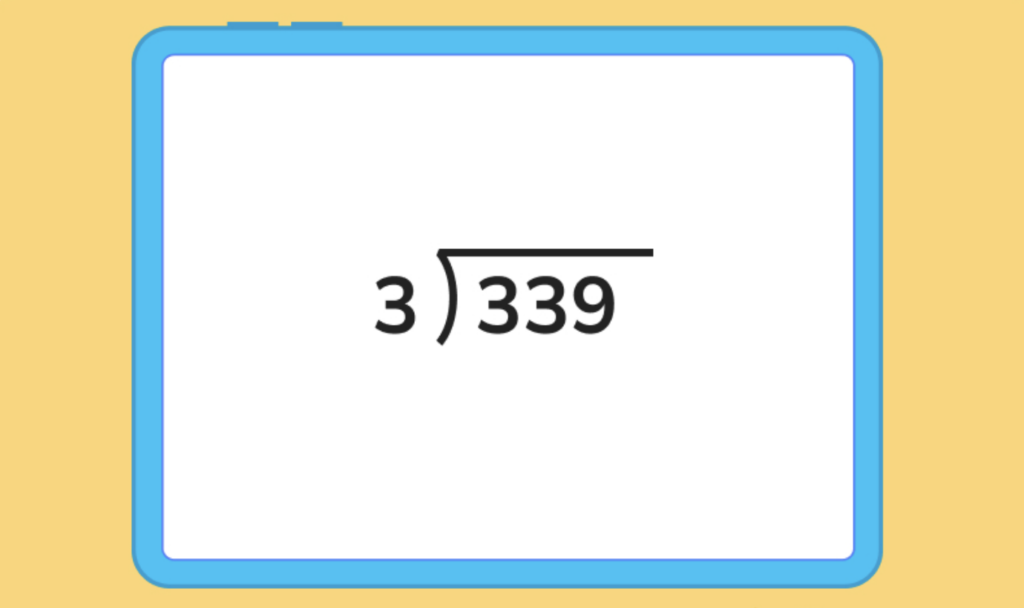
Solve 339 ÷ 3
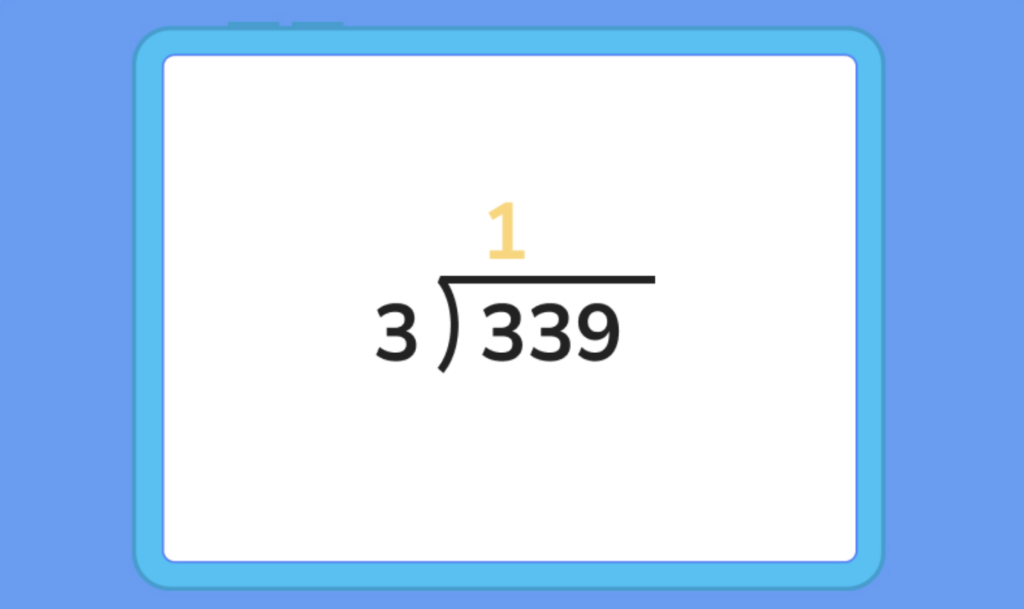
1. The 3 in the hundreds place of the dividend is divisible by 3, giving us a value of 1 to write first in the quotient.
2. Now, we can write a 3 underneath the 3 in the hundreds place, and subtract. This should give us a value of 0.
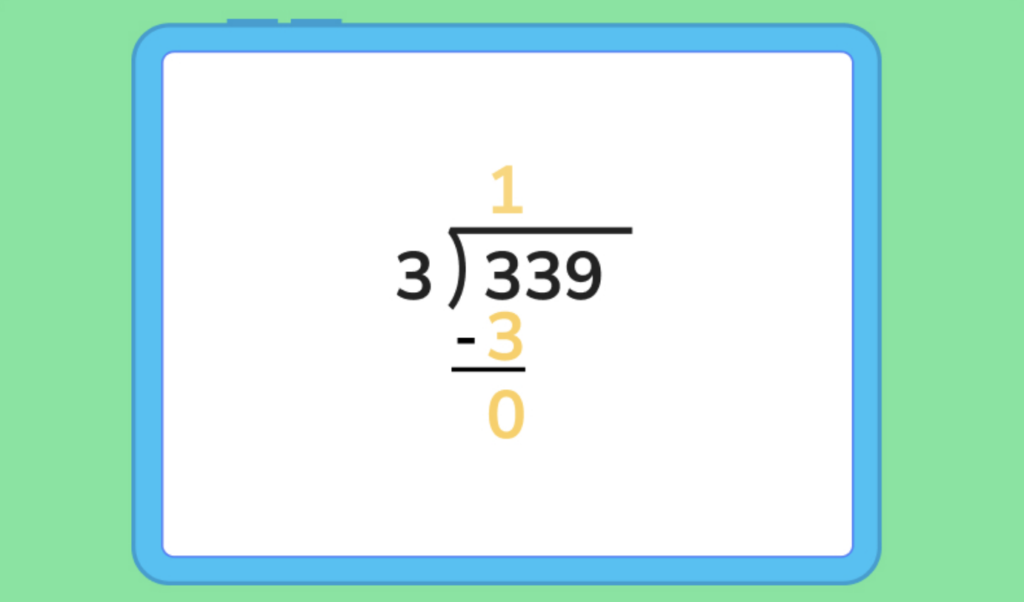
3. We can then drag the three in the tens place down next to our 0.
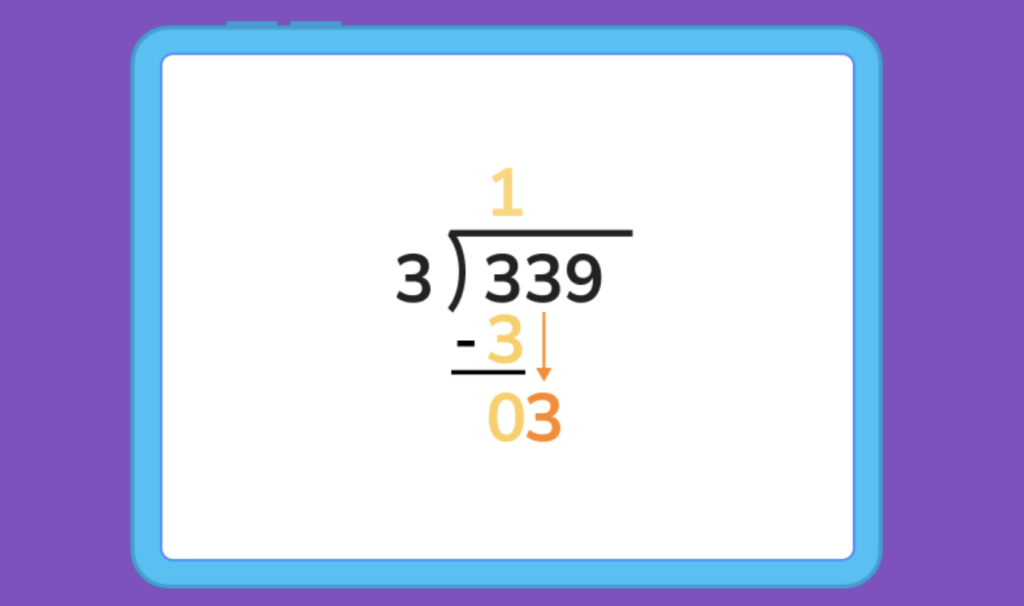
4. Let’s repeat the same process in step 1, since 3 is still divisible by 3. This will give us another 1 in the quotient, and a subtraction equation of 3 – 3 that gives another 0.
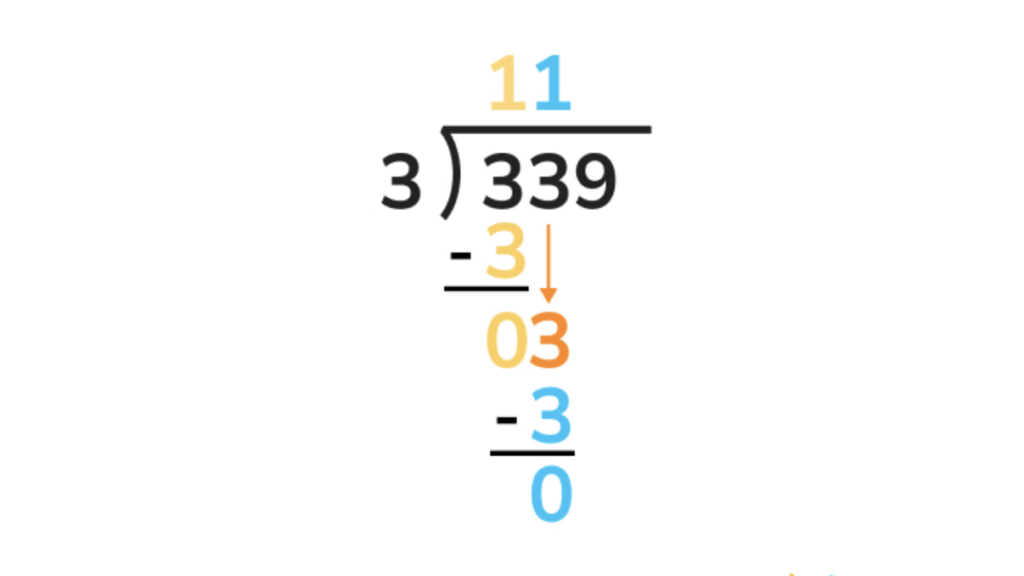
5. Now, let’s drag the 9 down next to our new 0. 9 is also divisible by 3. 93 = 3, meaning we can write a 3 as our last digit in our quotient. 3-3=0, meaning we’ve finished our long division. We should have a value of 113 in our quotient.
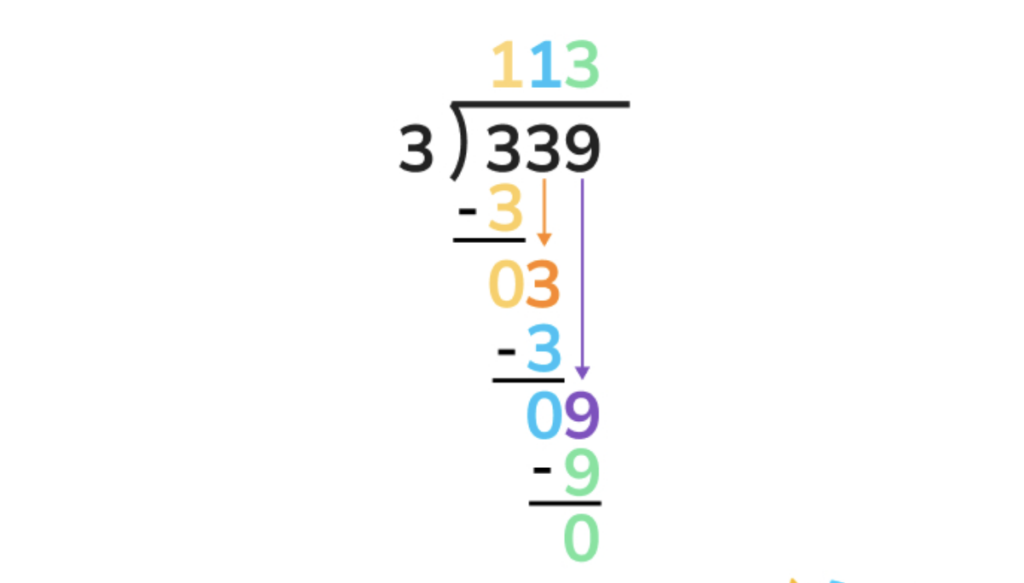
Ready to give it a go?
Now it’s your turn to put your long division skills to the test. Use your knowledge of long division to solve the following problems. Feel free to consult the guide if you get stuck.
Question 1: what is 645 ÷ 9?
Question 2: what is 422 ÷ 8?
Question 3: what is 218 ÷ 4?
Just remember to divide, multiply, subtract, bring that next number down and keep repeating that process. Long division is all about repeating the same steps over and over again until you can’t do any more division.
The hardest part is remembering to drag that next digit down so you can repeat the process. But if you can master those basic steps, you’ll begin to build some muscle memory that makes the process much easier.
For these problems, we check the first two digits of the dividend and see if they are divisible by our divisor. If the first two digits of the dividend are less than the divisor, we’ll need to consider the first three digits of the dividend instead.
Now we can follow the same steps. Figure out how many times we can multiply our divisor into our dividend, and subtract that value.
Long division is often more accurate than shorthand division, because the steps are written out plainly in front of us. This allows us to track our division through a step-by-step process, and continue dividing until we discover an exact remainder.
Think of long division as the most convenient and accurate way of dividing larger numbers. As you continue to learn mathematics, it’ll become an essential skill for solving more complicated problems.
This process might seem a bit more complicated, but it relies on the same rules and procedures we’ve been using this whole time.
Since we know that the quotient, remainder and divisor are all related to the dividend in some way, there is a mathematical procedure we can use to calculate each.
To find the dividend, simply multiply the quotient by the divisor, and add that product to your remainder.
Lesson credits
Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Taylor Hartley
Taylor Hartley is an author and an English teacher based in Charlotte, North Carolina. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching high school mathematics, ranging from Alegra 1 to AP Calculas. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!
The answer is 71 with a remainder of 6
How did we get here?
The answer is 52 with a remainder of 6
How did we get here?
The answer is 54 with a remainder of 2
How did we get here?
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
