Division won’t always give you a neat and clean answer – sometimes, you’ll be left with a remainder

Author
Taylor Hartley

Expert reviewer
Jill Padfield
Last updated: August 24, 2023


Division won’t always give you a neat and clean answer – sometimes, you’ll be left with a remainder

Author
Taylor Hartley

Expert reviewer
Jill Padfield
Published: August 24, 2023




Division won’t always give you a neat and clean answer – sometimes, you’ll be left with a remainder

Author
Taylor Hartley

Expert reviewer
Jill Padfield
Published: August 24, 2023


Key takeaways
Have your parents ever made dinner for the whole family thinking they’d cooked just the right amount, only to discover they’ve got an awkward amount of food left over? Well, in maths, you’ll occasionally encounter that exact same problem.
Don’t worry, though. Leftovers often mean you’ve got lunch for the next day – and remainders usually mean you’ve done something right!
Today, we’ll take an in-depth look at remainders: what they are, when they happen and what to do once you find one.
At first, you might feel like you’ve made a mistake when you’re left with a remainder, but rest assured, you (probably) haven’t messed up. Let’s dive in!
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Before we get going, there are a few key terms you’ll need to know to understand division. It’s tough talking about division if you don’t know these terms, so make sure you review them prior to continuing through this guide. You’ll need to know them as we talk about and practice finding remainders.
As the word suggests, a remainder is something left over, or ‘remaining’, after you’ve completed a division problem.
Once you’ve gone through all the steps of dividing, you might still have an extra value remaining. This always happens when one number is not completely – or evenly – divisible by another.
Don’t worry: you haven’t messed up! You’ve just reached the end of your calculation and it’s time to put your pencil down. That’s because remainders are part of the answer. Remember, the remainder should always be less than the divisor!
Look at the important terms to know. These terms are all key pieces of the division puzzle. You can determine the value of each of these pieces by using the others.
Take a look at this equation, which can help you quickly solve some of your problems if you have most of the pieces but need to find others:
Dividend = (divisor x quotient ) + remainder
Use this basic formula to calculate the divisor, quotient, or remainder, depending on which pieces you have and which you still need to find.
You can also rewrite this equation to find the remainder. Just switch a few things around:
Remainder = dividend — (divisor x quotient)
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day. Try it for free!

Using the equation above, we can calculate the value of our remainder in three easy steps.
First, it’s important that we understand each of the values in our problem, and which terms correspond to each of those values. That means you’ll need to identify what number represents the divisor, the dividend, the quotient and the remainder – and which values might be missing.
Now, we need to take a look at our dividend (the number that’s being divided), and see if there’s a specific value (our quotient) we can multiply by the divisor to get the dividend.
If there is no exact number to multiply by, we simply multiply to find the next smallest multiple.
A multiple is a number that can be divided by another number without a remainder.
For example:
Consider 70 ÷ 4. 70 is not completely divisible by 4, but 4 x 17 = 68. 68 is the largest possible multiple of 4 not higher than 70, so 17 (the number we multiplied by) will serve as our quotient.
Now that we’ve found the largest multiple, we can simply subtract it from our dividend. 70 – 68 = 2, so 2 will represent the remainder in our equation of 70 ÷ 4.
So, 70 ÷ 4 = 17 with a remainder of 2.
This can also be written as 17 R 2.
Remainders exist in long division, too. If you haven’t already reviewed our article on long division, make sure to check it out to get a more in-depth review prior to continuing.
The same basic steps apply.
The values multiplied by the divisor to calculate those multiples are written as digits that will eventually give you your quotient.
When you’ve divided your divisor into the last digit of your dividend, there may still be a value left over that can no longer be divided. And guess what? That’s your remainder.
1. Here, we can tell that the divisor will be the number of students (20), and the dividend will be the amount of stickers (134).

2. We look to see how many times 20 goes into our first digit 1. It cannot divide into 1, so we look to see if it can be divided into our first two digits, 13. Again, it cannot be divided into this value, so we look to see if it can be divided into our first 3 digits, 134, which it can.
3. 20 fits into 134 six times. 20 multiplied by 6 equals 120, and 134 – 120 = 14.
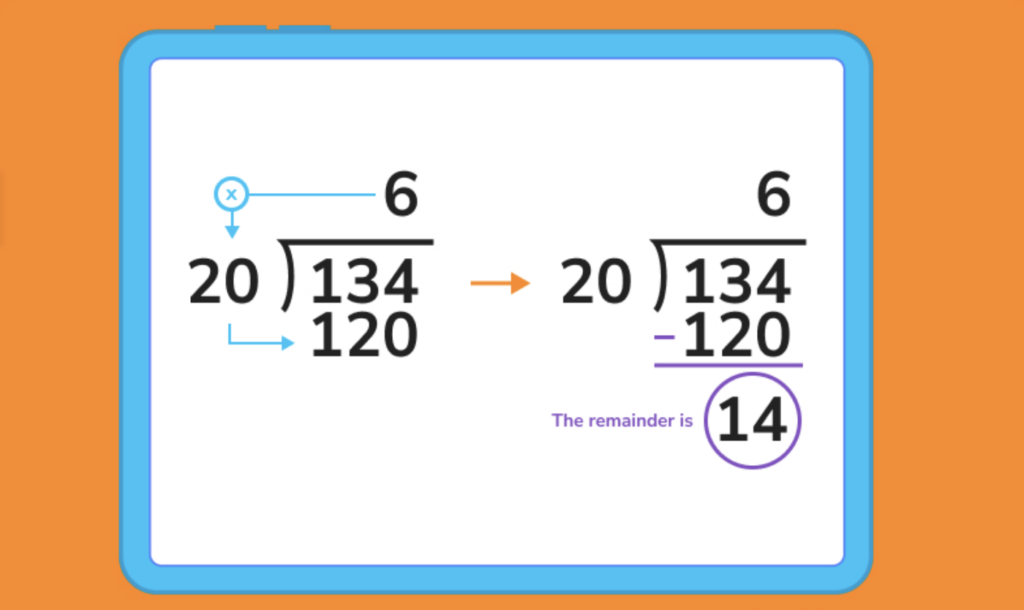
So, we know that each student receives 6 stickers, and there are fourteen stickers left over.

1. Here, we can use the equation from earlier to easily calculate the remainder.
2. Just remember that to find the remainder, you just need to multiply the divisor and the quotient, and subtract that product from the dividend.
3. 11 x 13 = 143
4. 147 – 143 = 4
5. The remainder is 4.
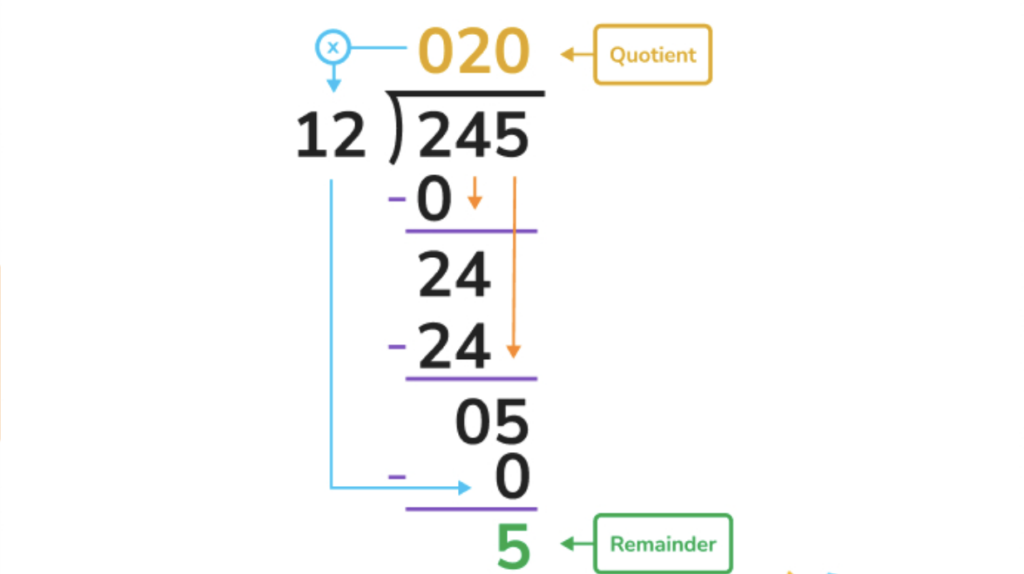
1. First, let’s define both the dividend and divisor. We’re dividing 245 by something else, so 245 is our dividend, and 12 is our divisor.
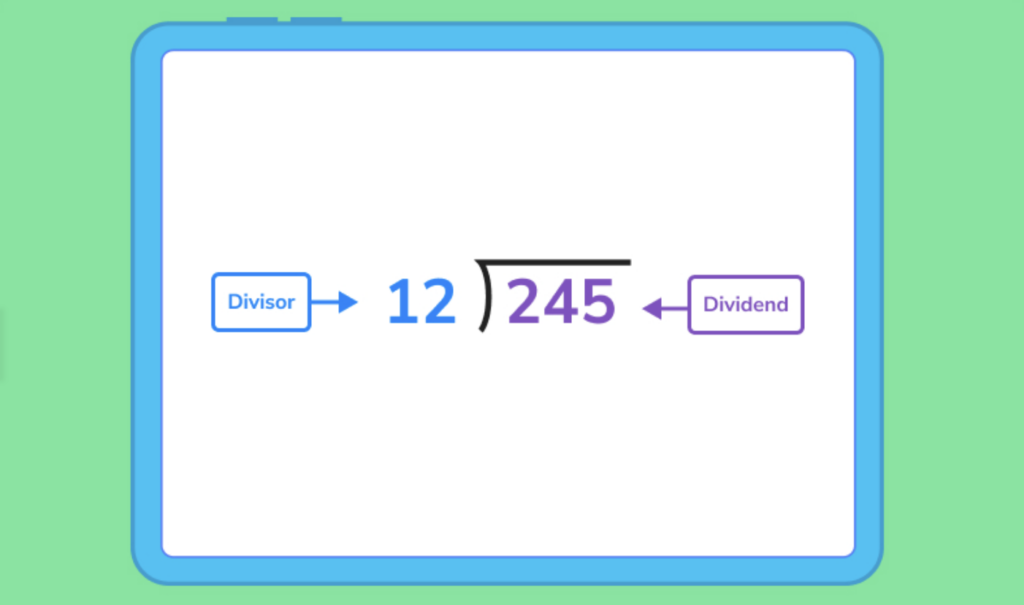
2. Now, let’s compare the 12 with the first digit of 245. We know 2 does not go into 2, so we see if it goes into the first 2 digits of the dividend, 24. 2*12=24, so we put a 2 above the tens place in our quotient, multiply it out, subtract, then bring down the next digit.
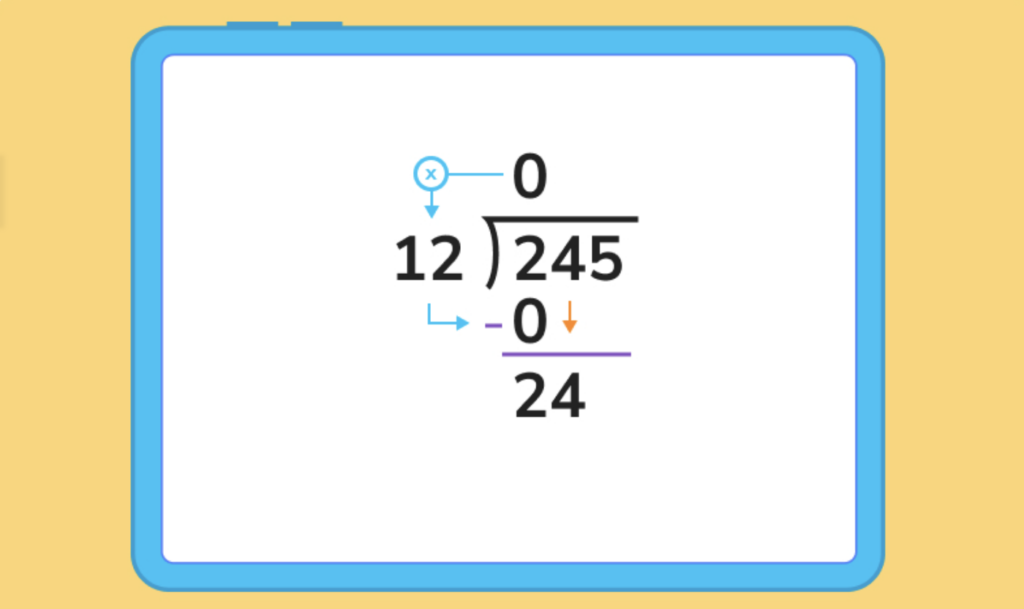
3. 2 – 0 = 2, and we can then drag the 4 down next to this 2 to make 24. 24 is exactly divisible by 12, so we can write a 2 in the quotient.
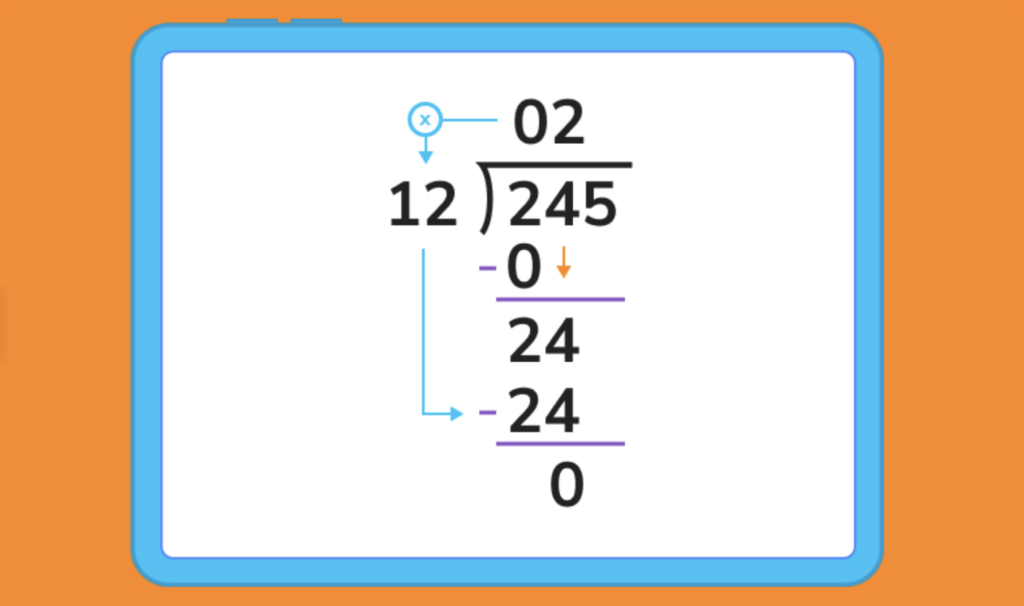
4. 24 – 24 = 0, and now we can drag the 5 down next to this zero. 12 is larger than 5, so we place another 0 in our quotient.

5. We multiply the 0 by 12, and subtract that answer from the 5. 0-5=5, so we are left with a quotient of 20 with a remainder of 5, or 20 R 5.
Ready to give it a go?
Now that we’ve run through a few problems together, it’s time for you to get some practice in by yourself. Feel free to look back at the explanations, equations, and definitions above to help you along the way.
Try your best not to get discouraged! Finding the remainder isn’t always easy, but it’s an important piece of the long division puzzle that you’ll need to master. So keep trying!
Question 1: find the remainder when 54 is divided by 3
Question 2: Jasmine has £63. She decides to divide it among her 5 friends, giving an equal amount to each. How much money does each friend get and how much is left over?
Question 3: Find the remainder when 89 is divided by 7
Question 4: Calculate the remainder when the dividend is 566, the divisor is 23, and the quotient is 24
Question 5: Find the remainder when 119 is divided by 10
The remainder is 0.
How did we get here?
Each friend gets £12, and there is £3 left over.
How did we get here?
The remainder is 5.
How did we get here?
The remainder is 14.
How did we get here?
The remainder is 9.
How did we get here?
Sign up for the DoodleMaths app today!
Turn maths into an adventure when you sign up for DoodleMaths.
You might not always get an exact amount when performing short or long division. It’s important to understand how leftover values are created, and how you should think of them in relation to both the divisor and the dividend.
Remainders are an essential part of understanding the majority of division problems you’ll encounter, as the majority of the time we divide the answer isn’t perfect. Remainders exist to provide more accurate quotients.
The remainder will always be less than the divisor. If your remainder is greater than your divisor, that means there is still more division you can perform, and your quotient is incomplete.
If the remainder is greater than the divisor, that means the divisor can still fit into the dividend another time. Continue to divide until the divisor is greater than the remainder to get the most accurate answer.
The remainder will only ever be 0 when the dividend is perfectly divisible by the divisor.
In other words, if the dividend is a multiple of the divisor, there won’t be any leftover values after dividing. In these situations, the remainder will be 0.
If you’re trying to calculate the remainder without performing standard long division, you can use the remainder theorem to find it instead.
However, this relies on you knowing the values of the dividend, divisor, and quotient beforehand. The equation is the following:
Remainder = dividend — (divisor x quotient)

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics,. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
What is division in maths?
Learn everything you need to know about division and have a go at some questions
How to do long division
Read our easy long division definition and explore our step-by-step guide
Roman numerals from 1 to 100
Learn the Roman numerals from 1 to 100 and have a go at some questions!
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: