Menu
Learn how to multiply fractions with ease!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Published: Sep 26th, 2023
Learn how to multiply fractions with ease!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Published: September 26th, 2023
Learn how to multiply fractions with ease!
Author
Taylor Hartley
Expert reviewer
Jill Padfield
Published: 26th of September, 2023
Key takeaways
The idea of multiplying fractions might seem daunting and complicated. But, the art of multiplying fractions can be mastered with just three simple steps. No more panicking before that dreaded math exam
Now, you’re probably thinking, “Well, when would I actually need to multiply fractions in the real world?”.
The truth is, we use fractions constantly without really thinking about it. Want to work out how to split that pizza evenly between your friends? You’ll need to have an understanding of fractions!
Looking to break that recipe in half because there’s no way you can eat 16 brownies? Similarly, you might want to triple the recipe for a school event. Both of these involve fraction multiplication.
So, how do you multiply fractions with whole numbers, and what steps are involved? Let’s take a closer look.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
When multiplying whole numbers, we are adding groups of the same number.
For example:
3 x 4 works out as 3 + 3 + 3 + 3, which equals 12.
Similarly, when you multiply fractions, you are grouping fractions together. The result can either be a whole number or another fraction.
For example:
½ x 3 would be ½ + ½ + ½ = 1 ½
The calculations are slightly different between problems that multiply fractions by whole numbers and those that multiply fractions together. The trick is to separate the bottom numbers and the top numbers of fractions into two different equations.
Before we dig into the steps involved in solving a fraction multiplication problem, it’s helpful to understand some of the terminology that’s commonly used:
There are also three main types of fractions that you need to be aware of:
Fractions have two parts; the numerator (top number) and the denominator (bottom number).
The numerators of both fractions need to be multiplied together, as well as the denominators to come up with the right answer. Then, if applicable, you can simplify your answer.
1. Multiply the numerators
Say you have a simple fraction calculation to work out. For example:
¼ x ⅔ = ?
The numerators are the numbers at the top. So, in this example, they would be 1 and 2. The first step to multiplying these fractions is to multiply both numerators. This would work out as:
1 x 2 = 2
2. Multiply the denominators
Now, you need to multiply the bottom numbers together, known as denominators. In the example above, this would work out as:
4 x 3 = 12
Then, we can put both of our answers together as their own fraction. This would be 2/12.
3. Simplify the product in the lowest form
2/12 still looks like a complicated fraction, doesn’t it? Luckily, we can simplify it!
All you have to do is divide the numerator and the denominator by the greatest common factor (number) that can divide into both numbers exactly. In our example, that number would be 2. So, now we divide:
Numerator: 2 ➗ 2 = 1
Denominator: 12 ➗ 2 = 6
We can put this into a fraction: ⅙. So, now we know the answer to our original equation in its simplest form:
¼ x ⅔ = ⅙
Pretty simple, huh? Now, let’s find out how to multiply a fraction by a whole number.
Want to have a go at some questions? DoodleMaths is an app that’s filled with thousands of fun, personalised exercises exploring the whole primary curriculum!
Accessible on tablets, mobiles, laptops and desktops, DoodleMaths creates each child a unique learning experience programme tailored to their needs, boosting their confidence and ability in maths.
Created by teachers, it sets work at just the right level for each child and includes visual explanations for every topic, letting them work independently. Try it free today!
1. Multiply the numerator with the whole number
Let’s say you have an equation that has both a whole number and a fraction. For example:
5 x ¾ = ?
Here, we need to group the fractions 5 times, which would look like this:
¾ + ¾ + ¾ + ¾ + ¾ = ?
This still looks a bit complicated, doesn’t it? Luckily, we can make the calculation simpler.
The first step is to turn your whole number into a fraction. This can easily be achieved by using your number as the numerator and adding 1 as the denominator (the denominator in any whole number is always 1).
In our example above, this would be 5/1
Then, you can multiply your numerators together, just as we did above. In our example, this would be:
5 x 3 = 15
2. The denominator remains the same
We’ve already changed our whole number into a fraction, so we know that our calculation for the denominators is 1 x 4, which equals 4. So, basically, our denominator stays the same.
3. Simplify the product in the lowest form
So, our answer is 15/4. Now, this is an improper fraction because the numerator is larger than the denominator.
There’s nothing wrong with improper fractions. In fact, many mathematicians prefer to use them over mixed numbers (a whole number and a fraction). However, in the real world, we tend to use mixed numbers more often, so it’s helpful to know how to convert it.
In our example, the denominator is telling us that the whole is split into 4 equal parts, known as quarters. The numerator is telling us that we have 15 parts altogether, or 15 quarters.
So, now we just need to work out how many wholes and fractions we have in their simplest form. Perhaps the easiest way to do this is with circles because they act as a great visual aid.
Remember, we need to find out how many whole circles we have when we split them into quarters, and also determine if there are any fractions left over.
In our example, we have 15 parts, with each whole circle being split into quarters. With the use of a visual aid, it looks like this:
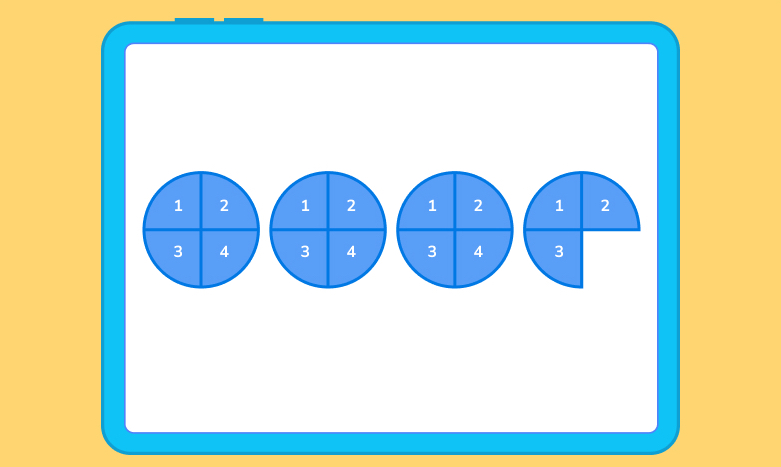
Now, we have our 15 quarters. We can clearly see that we have three whole circles and three-quarters of a circle left over. This can be written as 3 ¾. We have now successfully converted our improper fraction into mixed numbers!
Shapes are a great way to visually represent fraction multiplication problems because they help to illustrate how the numerators and denominators interact to produce the product (answer).
You can use circles, as we did above. But, perhaps the most common shape used to represent a fraction multiplication is a rectangle because it can easily be split into equal parts.
Here’s an example:
Using a fraction model to find the product of this multiplication problem: ¼ x ⅓
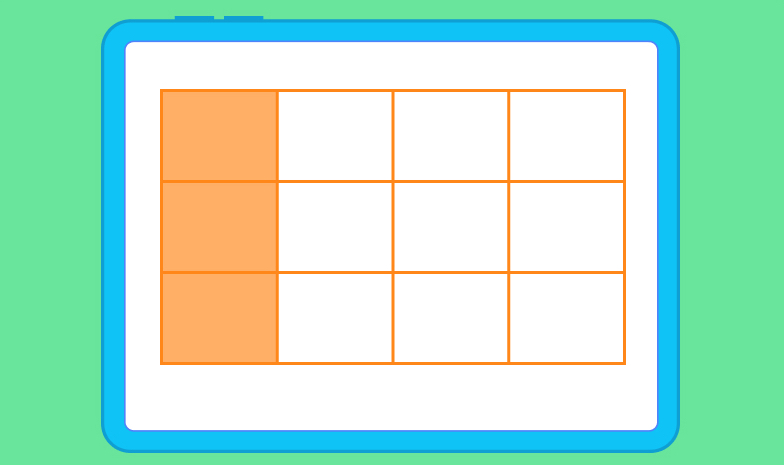
1. Draw a rectangle. You need to split it into four equal columns because the denominator in the first fraction is 4. The numerator is 1. So, simply shade in one of these columns as shown below:
2. The denominator in the second fraction is 3. So, now we add horizontal lines to represent this number:
3. The numerator in the second fraction is 1. So, shade in one row of your rectangle, like this:
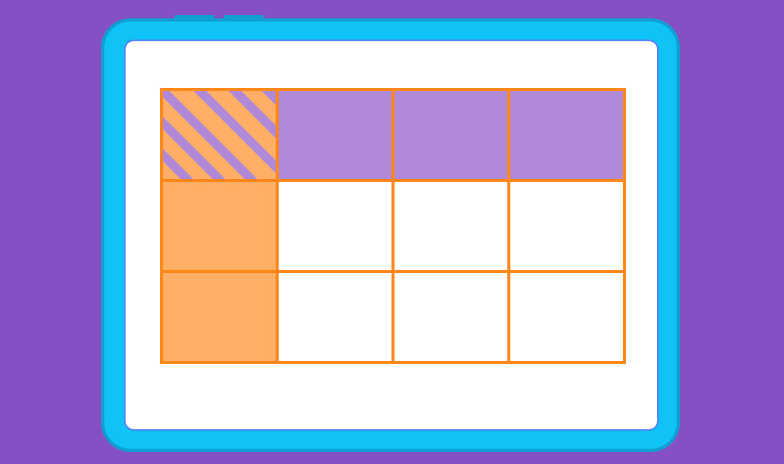
4. The numerator for the answer can be worked out by simply counting the blocks that have been shaded twice. In this case, it would be 1. The denominator is the total number of blocks in our rectangle, which would be 12.
So, the product of ½ x ⅓ = 1/12!
Multiplying fractions with a whole number can be calculated using repeated addition. Essentially, this involves grouping fractions to determine how many whole numbers and how many leftover fractions you have.
You can see this in the example above, where we used circles to work out our answer. Let’s try another example:
Mr. Bourne gave ¼ of a cupcake to 12 of his students. How many cupcakes did he give out?
Here, we are looking to work out 12 groups of ¼. This can be written out as 12 x ¼.
¼ is also known as a quarter, so we just need to work out how many cupcakes he gave out in total. We can write it out as:
¼ + ¼ + ¼ +¼ + ¼ + ¼ + ¼ + ¼ + ¼ + ¼ + ¼ + ¼ =
But, that seems very long-winded! Instead, we can use our circle diagrams. Remember, we need to end up with 12 quarters.
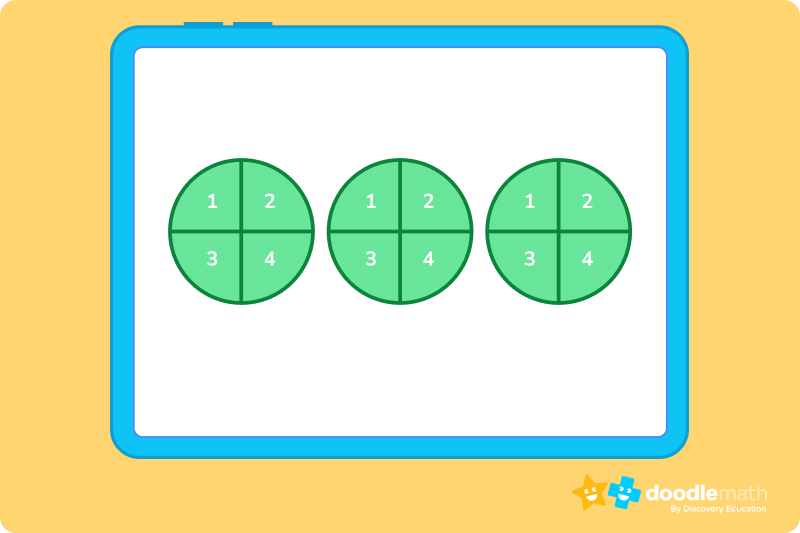
From this diagram, we can see that Mr. Bourne gave out 3 whole cupcakes.
If you’re multiplying two fractions together, the product will be the same, no matter what order you multiply them in. For example:
¾ x ¼ will have the same product as ¼ x ¾.
If a fraction is multiplied by 1, the product is the original fraction number.
If a fraction is multiplied by 0, then the product will always be 0.
When fractions are multiplied, the numerator and the denominator are multiplied separately. The numerator of the first fraction is multiplied by the numerator of the second fraction. Then, the same process is repeated with the denominators.
Remember that when we multiply a fraction by a whole number, we change our whole number to a simple fraction, with 1 as the denominator. This would be 2/1. Then, we simply multiply the numerators together:
3 x 2 = 6
When it comes to our denominators; 2 x 1 = 2, so the denominator in our answer remains as 2.
Therefore, the final answer to our equation is 6/4, which can be simplified to 3/2 because both numbers can be divided by 2.
Now that we are multiplying two fractions, we already have our numerators and denominators in place. Remember, we need to treat these as two different multiplication problems:
Numerators: 1 x 3 = 3
Denominators: 7 x 5 = 35
So, we end up with 3/35. The only factor that fits into both the numerator and the denominator is 1. Therefore, this fraction is already in its simplest form
The right answer is FALSE because the numerator is not a larger number than the denominator.
Ready to give it a go?
Now it’s time to put your knowledge to the test! Work through the following problems on your own and see how you do. Feel free to look back through this guide if you get stuck, or go through the practice problems again.
Don’t be discouraged if you struggle. Remember: practice makes perfect!
Click to reveal the answer.
The answer is 2.
The answer is 3/5.
The answer is ¼.
The answer is TRUE.
The answer is ⅜.
The answer is 2
How did we get here?
The answer is 3/5
How did we get here?
The answer is ¼
How did we get here?
The answer is TRUE
How did we get here?
The answer is ⅜
How did we get here?
Create a DoodleMaths account today!
Gain access to thousands of fun, interactive questions and games exploring the whole primary curriculum.
Like everything, practice makes perfect and it might take a little bit of time before you master multiplying fractions. However, when you break it down into simple steps, it’ll be much easier to understand!
Fraction multiplication can be achieved in three simple steps:
Equations that involve a whole number and a fraction are known as mixed fractions.
For example, 7 x ½. This essentially means that you have to find the product of ½ + ½ + ½. + ½ + ½ + ½ +½.
To do this, change your whole number into a fraction, with 1 as the denominator. In our example, this would be 7/1. Now you can multiply your numerators and then your denominators to find your answer.
For more complicated mixed fraction equations, you can also consider using visual models and dividing them into fractions — just like you would cut a whole pizza!
If you’re multiplying a fraction with another fraction, then you need to multiply the numerators together (top numbers) and the denominators together (bottom numbers).
However, if you’re multiplying a fraction with a whole number, the denominator will appear to stay the same since the denominator of any whole number is 1.
Rational and irrational numbers
Learn about the differences between rational and irrational numbers
Roman numerals from 1 to 100
Learn the Roman numerals from 1 to 100 and have a go at some questions!
Lesson credits
Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst and is earning a masters degree in business administration.
Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics. She is currently working as a Business Analyst and is earning a masters degree in business administration.
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
