What is an integer?

Q: What are consecutive integers?

Consecutive integers are integers that follow each other in order from smallest to largest by 1.

In this guide, learn all about the properties of integers and how to use them!

Author
Tess Loucka

Published
November 3, 2023

What is an integer?

In this guide, learn all about the properties of integers and how to use them!

Author
Tess Loucka

Published
Nov 3, 2023

What is an integer?

In this guide, learn all about the properties of integers and how to use them!

Author
Tess Loucka

Published
Nov 3, 2023

Key takeaways

Integers are a set of numbers that include positive numbers, negative numbers, and zero. Fractions and decimals aren’t considered integers.
The sign put before an integer, positive or negative, affects the result of the problem that the integer is a part of.
There are 7 properties of integers that are always true and can be used to simplify questions.

Table of contents

You might not realise it, but you use integers every single day!

When you’re counting up your pocket money, checking how many more pages are left in a chapter you’re reading or even seeing how far you have to scroll through the TV channels to get to the programme you want to watch, you’re using integers.

To put it simply, an integer is a whole number. In school, you work with whole numbers all the time. But what makes integers a little more complicated is that they can also be negative numbers.

There are many rules and properties to remember when working with integers, but before we get started, what exactly is an integer?

Integer definition

An integer is any positive or negative round number, including zero.

A number with a fraction or decimal can’t be an integer, because it’s not a round number. After all, the word ‘integer’ literally means ‘whole’ in Latin, so the integer definition makes sense.

Types of integers

Zero: zero is a whole number that marks the point between positive numbers and negative numbers. It’s not positive or negative on its own.
Positive integers: positive integers are any whole number greater than zero.
Negative integers: negative integers are any round number less than zero.

Unlock unlimited maths questions

Put your skills to the test with fun exercises + maths games that are proven to boost ability!

Try DoodleMaths for free!

Select a year group

Number
Shape, space and measure
Patterns
Number and place value
Addition and subtraction
Multiplication and division
Operations (ASMD)
Fractions
Measure
Shape/geometry
Statistics
Ratio and proportion
Algebra
Probability

Integers on a number line

To visualise integers, place them on a number line! A number line is a horizontal line that goes on for infinity on both sides. Numbers are placed on the line in relation to each other using equally distanced lines and spaces.

When setting up a number line, 0 is placed in the middle. As numbers get bigger, they move to the right. Smaller numbers go to the left.

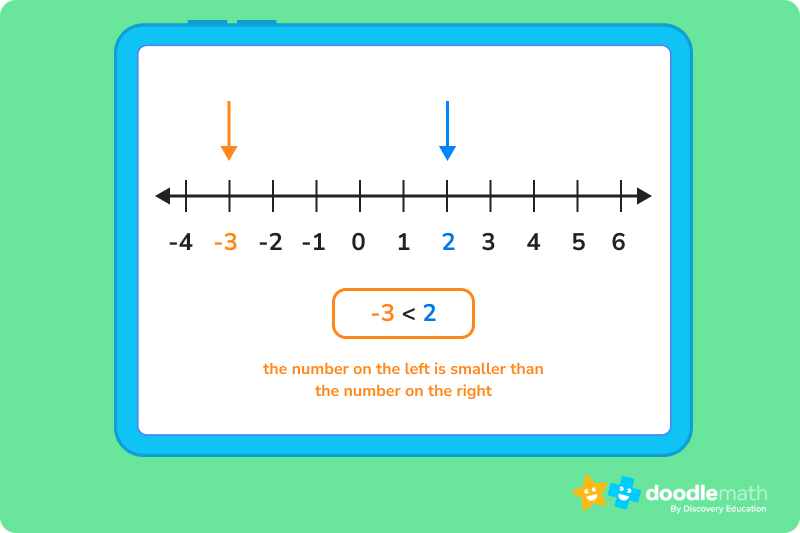
When placing integers on a number line, you often start off with an integer set. Integer sets are lists of integers notated as Z = {list of integers}

Here’s an example integer set: Z = {-5, -2, 1, 3, 6}

As you get into more advanced integer graphing, you may come across the term greatest integer function. The greatest integer function is denoted as [x] = y. In this function, y is the largest integer that is less than or equal to x. Think of it as rounding down.

For example, [3.4] = 3 because 3 is the largest integer less than or equal to 3.4

[-3.4] = -4 because -4 is the greatest integer less than or equal to -3.4 (remember to move left on the number line!)

Integer operations

So, what is an integer operation, and how do you use integers in maths problems?

Integer operations are basic operations that can be done using integers.

To complete these operations, you’ll need to use the integers’ absolute values. The absolute value of an integer is the number value, or the distance away from zero. As a result, absolute value will always be positive.

So, 2 would be the absolute value of both |2| and |-2|. The absolute value of both |-43| and |43| is 43.

Adding and subtracting integers

Adding integers of the same sign (positive or negative) will always result in an integer with that same sign.

(+3) + (+8) = +11

(-3) + (-8) = -11

Adding integers with different signs will result in an integer with the same sign as the number with the larger absolute value. To solve these questions, subtract the integers’ absolute values and use the sign of the number with the larger absolute value.

(+3) + (-8) becomes |8| – |3|, which is 5. The 8 is larger than the 3, and it is negative, so 5 becomes -5.

(-3) + (+8) also becomes |8| – |3|, which is 5. The 8 is larger, but it is positive, so 5 becomes +5.

When subtracting integers, change the sign of the second number and add the numbers together.

(+3) – (+8) becomes (+3) + (-8) = -5

(-3) – (-8) becomes (-3) + (+8) = 5

Multiplying integers

When multiplying integers, the result will be positive if both integers have the same sign. That’s true whether the sign is positive or negative. The result will be negative if both integers have different signs.

(+3) x (+8) = +24

(+3) x (-8) = -24

Dividing integers

The rules for dividing integers are the same as they are for multiplying them. If both integers have the same sign, the result is positive. If both integers have different signs, the result is negative.

(+10) ÷ (+5) = +2

(+10) ÷ (-5) = -2

Explore integers with DoodleMaths

DoodleMaths is an interactive maths app that’s filled with questions covering integers, shapes and more!

Specifically designed for ages 4-14, it creates every child a unique learning experience tailored to their needs, building their skills in as little as six weeks. Try it for free today!

Create a free Doodle account

Properties of integers

Closure property

According to this property, when you add, subtract or multiply two integers together, the result will always be an integer. Dividing any two integers does NOT always result in an integer.

Eg. 8 + 4 = 12

8 – 4 = 4

8 x 4 = 32

8 / 4 = 2, but 4 / 8 = ½ or .5 (fractions and decimals are not integers)

Associative property

According to this property, rearranging the grouping of integers doesn’t change the result when performing addition or multiplication.

In other words, a + (b + c) = (a + b) + c

Similarly, a x (b x c) = (a x b) x c

The placement of the parentheses doesn’t matter. The answer will always be the same. However, this is not true for subtraction or division.

Commutative property

Similar to the associative property, this property states that the order of integers in an addition or multiplication problem doesn’t affect the result.

So, a + b = b + a and a x b = b x a

Distributive property

This property states that when using the form a (b + c), the integer in place of “a” can be distributed to “b” and “c” to become (a x b) + (a x c).

Ex. 3 (2 + 8) = (3 x 2) + (3 x 8) = (6)(24) = 30

Additive property

This property states that adding two of the same integers together with different signs always results in 0.

Ex. 2 + (-2) = 0. In this case, -2 is the additive inverse of 2.

(-2) + 2 = 0. In this case, 2 is the additive inverse of -2.

An additive inverse is any integer that, when added to another integer, results in 0.

Multiplicative inverse property

This property states that any given number multiplied by itself over 1 is equal to 1. This is written as a + a/1 = 1.

Ex. 5 x 5/1 = 1

Identity property

This property states that any integer plus 0 is equal to the integer itself, while any integer multiplied by 1 is equal to the integer itself.

Ex. 8 + 0 = 8

8 x 1 = 8

Integer practice questions

Click on the boxes below to see the answers!

Question 1: What is (+9) - (-3)?

Answer: +12

When subtracting two integers, change the sign of the second integer, and add the integers together. (+9) – (-3) becomes (+9) + (+3), which is equal to +12 or 12.

Question 2: What is (-12) ÷ (-3)?

Answer: +4

When dividing two integers with the same sign, the result will always be positive. Three goes into 12 four times, so the answer is +4 or 4.

Question 3: What is ((+2) x (-3)) + (+7)?

Answer: +1

Solve what is within the parentheses first. Multiplying two integers with different signs results in a negative number. So, (+2) x (-3) equals -6. Now, add +7 to -6 to get +1 or 1.