Read on to understand how to find the least common multiple in easy-to-understand terms.
Author
Taylor Hartley
Expert Reviewer
Jill Padfield
Published: July 2024
Read on to understand how to find the least common multiple in easy-to-understand terms.
Author
Taylor Hartley
Expert Reviewer
Jill Padfield
Published: July 2024
Read on to understand how to find the least common multiple in easy-to-understand terms.
Author
Taylor Hartley
Expert Reviewer
Jill Padfield
Published: July 2024
Key takeaways
Table of contents
Maths, despite how intimidating it may seem at first, is really just about finding commonalities. Multiples and factors go a long way to help you understand how different numbers are related and how you can predict their behaviours reliably.
The least common multiple (LCM) is just one of the ways mathematicians and everyday people understand the relationships between numbers. By figuring out these connections, you can unlock the many ways numbers work with one another.
To understand the least common multiple, you need to remember what a multiple is. As you may have learned before, a multiple of a number is the product you get when you multiply that number by any other number.
If you want to find the multiples of 3, you would simply go down the line 1, 2, 3, 4, and so on, multiplying 3 by each number to find the products. That means that the multiples of 3 are 3, 6, 9, 12 and on.
For LCM, though, you fortunately just need to find the smallest multiple that two numbers share.
For example, the LCM of 3 and 5 is 15. The multiples of 3 are 3, 6, 9, 12, 15, 18. And the multiples of 5 are 5, 10, 15, 20… 15 is the lowest number both of those lists have in common, so 15 is the LCM of 3 and 5.
You’ve got a few options when you sit down to find the LCM of two numbers:
Some options are very simple, but they take a long time. Others are much quicker, but they do require you to understand factoring. Like with most maths concepts, as your skills and understanding grow, the quicker and more confident you’ll become. Start with the simple long way and gradually work your way to the more complex and quicker methods.
The simplest way to find the least common multiple of two numbers is to just list out the multiples of those numbers and look for the lowest number both lists share. This may take the longest of all the methods, but all you need to know is how to multiply to figure this one out.
Let’s play it out, and see how this is done. You want to find the LCM of 4 and 5.
Start by making three rows on your paper, one for the numbers you will multiply by (the multipliers: 1, 2, 3, and so on), one for multiples of 4, and one for the multiples of 5.
Once you have the table planned out, find the multiples of both numbers and fill in the table one multiplier at a time. Once you find a product that both lists share, you can stop. That will be your LCM.
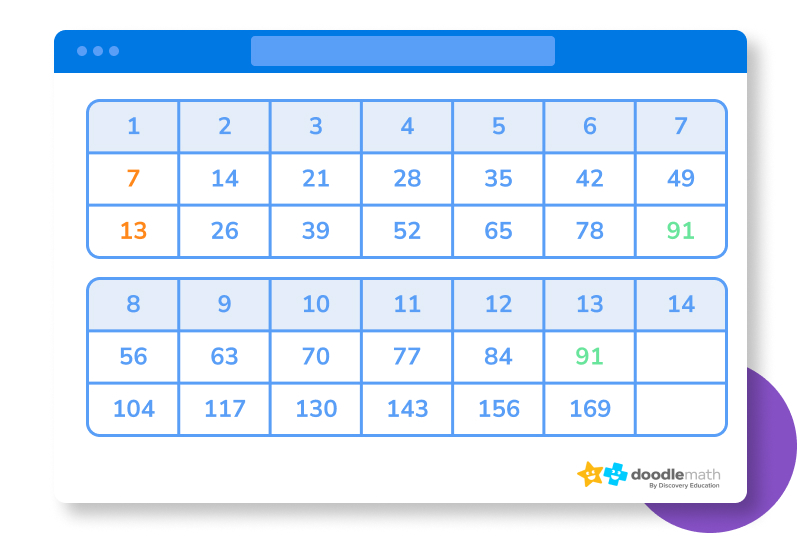
After all that maths, you can see that the lowest number that both lists share is 20. That means your LCM is 20! Let’s look at one more example. How about the LCM of 7 and 13?
As before, write out your table and start figuring out the multiples of 7 and 13 — up to the multiplier 7. This is because 7 x 13 will be a common multiple for sure.
Unlock unlimited maths questions
Put your skills to the test with fun exercises + maths games that are proven to boost ability!
Want to learn more about finding the least common multiple? DoodleMaths is an award-wining maths app that’s proven to double a child’s rate of progression with just 10 minutes of use a day!
Filled with fun, interactive questions covering the whole curriculum, it creates each child a unique work programme tailored to their needs, boosting their confidence and skills in maths. Try it free today!
Listing multiples can be time-consuming, but, fortunately, there are much faster methods. The next option is quicker, but you do need to know what prime numbers are.
Prime numbers are numbers that can be divided evenly only by 1 and the number itself. For instance, 13 is a prime number because you can only divide 13 evenly by 1 and 13.
As you will see in a moment, these prime numbers can come in handy when trying to find the LCM between two numbers.
Put together a table with prime numbers in the left column and the two numbers you are trying to find the LCM for on the right separated by a comma or a line. Start dividing each number by the smallest prime number you can, moving on to the next highest when you need to. If one of the two numbers cannot be evenly divided by the prime number, keep it the same and move on down the line until you get 1 for both numbers. This sounds complicated! Don’t worry– it’s easier to see this in action.
Let’s use this method to find the LCM of 12 and 20.
Now that you have a row with two ones, go through the prime numbers on the left and multiply them together. The product is your LCM.
2 x 2 x 3 x 5 = 60, so 60 is the LCM of 12 and 20
Prime factorisation is a slightly faster version of the last option. You will do this by factoring both numbers you are trying to find the LCM of down to the prime factors.
Let’s go with 24 and 44.
To find the prime factorisation of 24, begin by finding two factors that multiply to give you 24. Let’s say we use 8 x 3. Three is a prime number, so we don’t need to break that one down any more. Eight is a composite number, so we need to break it down into two factors again. This time, we can use 2 x 4. Two is a prime number, so we can set it aside. Four is composite, so we break it down again into 2 x 2. Now, we have all prime numbers as factors of 24.
So, the prime factorisation of 24 is 2 x 2 x 2 x 3, which can also be expressed as 2³ 𝑥 3.
Use this same method to find that the prime factors of 44 are 22, 2, and 11, which can be expressed as 2² and 11. You can start by dividing 44 by 2, which will get you 22 and 2 as factors. Two is prime, so you are done with that one. Twenty-two can be divided further into 11 and 2. Both of those are prime, so you are left with 2, 2, and 11 as factors.
Now, look at all the factors you got for both numbers together. We have 2³ 𝑥 3 for one, and 2² 𝑥 11 for the other. To find the LCM, we will multiply the factors, leaving out any that overlap. For this example, 3 and 11 don’t have any overlap, so we will use them both. For the 2’s, the overlap is 2², so we will only use the 2³.
You now have 2³, 3, and 11 set aside. Now you multiply those together to find the LCM.
2³ x 3 x 11 = 264. That’s your LCM.
If you can find the highest common factor of two numbers, you can easily find the lowest common factor. You can use the formula: LCM = the product of two numbers ÷ the HCF.
If you need help with finding the HCF, make sure to check out our lesson, but, in short, you find the highest common factor of two numbers by factoring both numbers and looking for the largest number in common.
Let’s try this out with 24 and 36.
Twelve is the greatest common factor of both 24 and 36. 12 x 2 = 24 and 12 x 3 = 36.
Now, according to our formula, you multiply 24 and 36 together and divide the product by 12, the HCF.
(24 x 36) ÷ 12 = 72. That means the LCM of 24 and 36 is 72.
Try DoodleMaths for free!
Select a year group
1. Find the LCM of 8 and 20 by listing multiples.
The LCM is 40.
2. Find the LCM of 9 and 21 by dividing prime numbers.
3 x 3 x 7 = 63, so that is the LCM.
3. Find the LCM of 25 and 42 with prime factorisation.
The prime factors of 25 are 5 and 5, expressed as 5².
The prime factors of 42 are 2, 3, and 7.
Multiply 5², 2, 3, and 7 together to get 1050. That’s the LCM.
The GCF of both 32 and 80 is 16.
(32 x 80) ÷ 16 = 160. 160 is the LCM.
Ready to give it a go?
Time to try this out on your own. Remember to look back at the lesson for guidance. If the maths doesn’t seem to be working out, retrace your steps, and see where you maybe missed a step or miscalculated.
Click to reveal the answer.
The answer is 36.
The answer is 2550.
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
LCM stands for Least Common Multiple. It is the smallest number that is a multiple of two or more numbers.
To find the LCM, you can list out the multiples of each number until you find a number that is on both lists. You can also use division, prime factorisation, and highest common factor to find the LCM.
LCM can be used to solve problems involving time, money, and distance. For example, you can use LCM to find the least common number of hours that two people can hang out or the least common amount of money that two people can pitch in for dinner.
Some common mistakes people make when finding LCM include:
Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!
24
How did we get here?
36
How did we get here?
150
How did we get here?
2340
How did we get here?
2550
How did we get here?
Lesson credits
Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.
Jill Padfield
Jill Padfield has 7 years of experience teaching mathematics, ranging from Algebra to Calculus. She is currently working as a Business Analyst, working to improve services for Veterans while earning a masters degree in business administration.
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
