Read a simple prime number definition, discover how we use them in maths and explore a list of prime numbers from 1 to 100!
Author
Tess Loucka
Published
October 30, 2023
Read a simple prime number definition, discover how we use them in maths and explore a list of prime numbers from 1 to 100!
Author
Tess Loucka
Published
Oct 30, 2023
Read a simple prime number definition, discover how we use them in maths and explore a list of prime numbers from 1 to 100!
Author
Tess Loucka
Published
Oct 30, 2023
Key takeaways
Prime numbers are one of the most important building blocks in all of maths, and form the foundation of many mathematical discoveries throughout the centuries.
The idea of prime numbers dates back to around 1550 BC, with the Rhind Mathematical Papyrus from ancient Egypt.
However, the first definitive study of prime numbers took place in ancient Greece, when the Greek mathematician Euclid made a clear distinction between prime and composite numbers. His discoveries became the basis of maths as we know it!
Today, prime numbers are used in encryption and decryption software, rotor machines, telecommunication codes and hash tables that organise data.
Primality, or the property of being prime, is integral to so many areas of maths and real life situations. But, what exactly is a prime number? Let’s take a look!
A prime number is any positive number that can only be divided by itself and the number 1.
Take 3 for example. Three is only divisible by 1 and 3. That makes 3 a prime number!
Now let’s look at the number 6. Six is divisible by 1, 6, 2 and 3. It has four factors, meaning it’s not a prime number.
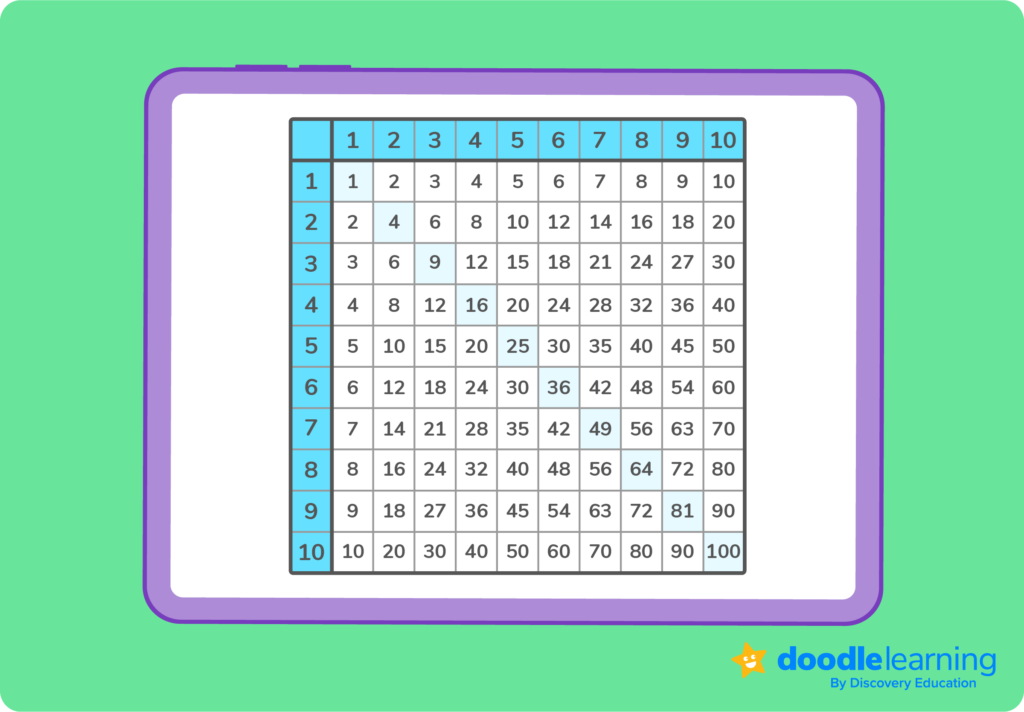
You can quickly figure out what a number’s factors are by using a multiplication square.
Fun fact: When answering a question in DoodleMaths, the award-winning maths app, you can pull up a multiplication square at any time for assistance!
Get 1 FREE month of Doodle!
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Try DoodleMaths for free!
Select a year group
If you’re ever unsure if a number is prime, look at the list of prime number properties below.
This is the classic definition of prime numbers and the first thing you should look for when figuring out if a number is prime.
Prime numbers are always positive because positive numbers are the only numbers that can have only two factors. 3 has two factors, 1 and 3. On the flip side, -3 has four! They are 1, -3, -1 and 3.
Prime numbers are whole numbers that can’t be divided by any other whole numbers besides 1 and itself.
The only factor of 1 is 1! That means 1 has only one factor, and prime numbers must have two. Because of this rule, 0 is also not a prime number.
Prime numbers, besides 2, have to be odd. After all, even numbers are divisible by 2, so they’ll always have more factors than itself and the number 1.
Meet DoodleMaths, the award-wining maths app that’s proven to boost a child’s rate of progression in as little as six weeks!
Filled with fun, interactive questions covering the whole curriculum, it creates each child a unique work programme tailored to their needs, building the confidence and skills in maths. Try it for free today!
There are 25 prime numbers up to 100.
The prime numbers list up to 100 is as follows: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
You can figure out what numbers up to 100 are prime by using the Sieve of Eratosthenes:
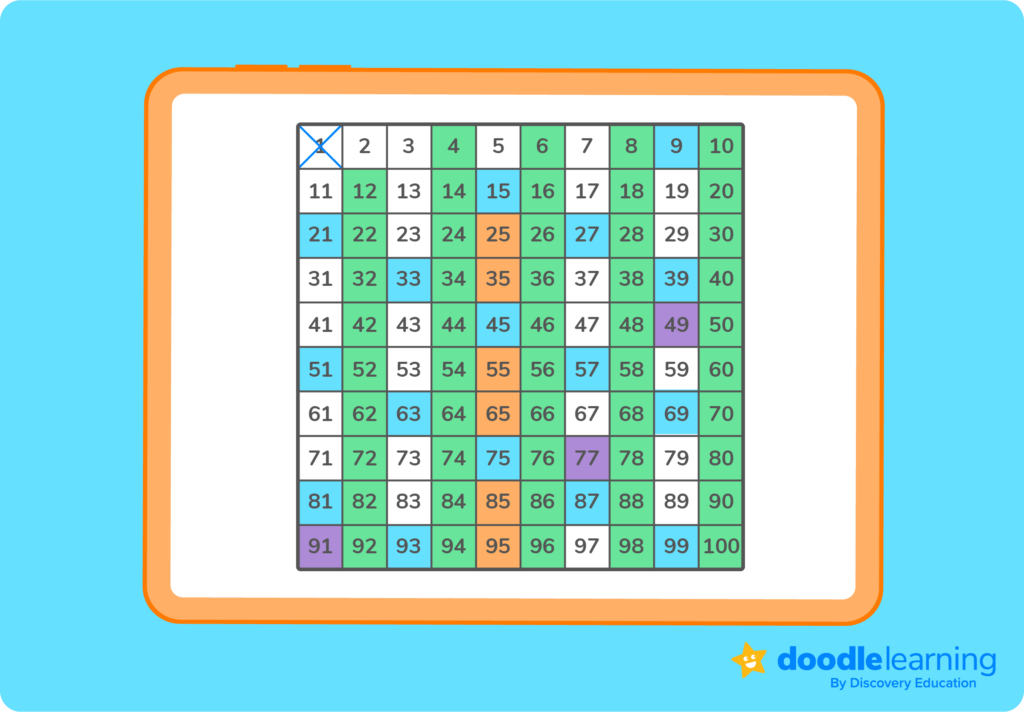
To figure out if a specific number between 1-100 is prime, there’s another technique you can try.
If the number is greater than 2 and is even, it’s not prime. If the number ends in a 5, it’s not prime.
Next, determine whether the number is divisible by 3 or 7. If it is, it’s not prime.
Take the number 83 for instance. Is it a prime number?
Well, let’s check!
Is it even? No…
Does it end in 5? No…
Is it divisible by 3? 8+3=11. 11 isn’t divisible by 3, so 83 isn’t either. So no…
Is it divisible by 7? No…
So, 83 is a prime number!
If you answer YES to any of these questions, the number is composite.
Now what about numbers above 100?
There isn’t a strict pattern that prime numbers follow, meaning there isn’t one technique or formula you can use to find all prime numbers.
However, if you’re interested in finding prime numbers between 101-200, just determine whether a number is divisible by 2, 3, 5, 7, 11 and 13. If the number is not divisible by any, it’s prime!
Prime and composite numbers make up all positive numbers (also known as integers).
All whole numbers besides 0 and 1 are either prime or composite. Since a prime number is a whole number with only two factors, composite numbers are whole numbers with 3 or more factors.
8 is a composite number because it is divisible by 1, 8, 2, and 4.
7 is a prime number because it is only divisible by 1 and 7.
Keep in mind that negative numbers are neither prime nor composite!
A prime number is any positive number greater than 1 that is divisible only by 1 and itself.
For finding prime numbers up to 100, use the Sieve of Eratosthenes. You can also ask yourself four questions:
If you can answer NO to each question, the number is prime.
For numbers between 101 and 200, ask yourself whether the number is divisible by 2, 3, 5, 7, 11 and 13. If it is not, it’s prime.
The number 1 only has one factor, 1. That means it doesn’t count as a prime number or a composite number.
The number 2 is a prime number because it can only be divided by 1 and itself.
The prime numbers up to 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Lesson credits
Tess Loucka
Tess Loucka discovered her passion for writing in high school and has not stopped writing since. Combined with her love of numbers, she became a math and English tutor, focusing on middle- and high-school-level topics. Since graduating from Hunter College, her goal has been to use her writing to spread knowledge and the joy of learning to readers of all ages.
Tess Loucka
Tess Loucka discovered her passion for writing in high school and has not stopped writing since. Combined with her love of numbers, she became a math and English tutor, focusing on middle- and high-school-level topics. Since graduating from Hunter College, her goal has been to use her writing to spread knowledge and the joy of learning to readers of all ages.
Rational vs irrational numbers
Explore the differences between rational and irrational numbers
What is standard form?
Discover how standard form helps us represent numbers and equations clearly
What is place value? The ultimate guide
Learn all about place value and take a look at some examples!
All rights reserved.
Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:
