What is prime factorisation?

Did you know we have the power to change the way numbers are represented by using the prime factorisation method? Learn all about prime factorisation in this handy guide!

Author
Amber Watkins

Published
November 7, 2023

What is prime factorisation?

Did you know we have the power to change the way numbers are represented by using the prime factorisation method? Learn all about prime factorisation in this handy guide!

Author
Amber Watkins

Published
Nov 7, 2023

What is prime factorisation?

Did you know we have the power to change the way numbers are represented by using the prime factorisation method? Learn all about prime factorisation in this handy guide!

Author
Amber Watkins

Published
Nov 7, 2023

Key takeaways

Prime factorisation is one of the most fundamental ideas in maths, and we use it often in our everyday lives without realising it. It simply means breaking down a number using its prime factors.
In KS2, we learn the foundational skills of factors and prime numbers, which help us to understand more complicated elements of prime factorisation.
Prime factorisation also requires a good understanding of basic multiplication and division skills.

Table of contents

We all love chameleons. Why? Because they are able to change their appearance based on their environment. A chameleon can make itself blend in with a tree or leaves, and can even change into different colors.

Did you know we can do something similar with numbers? They can’t change into different colors or resemble a tree, but we can change the way they are represented in maths depending on what we need them for.

One of the most common ways numbers can change the way they are represented is through prime factorisation. What is prime factorisation?

Prime factorisation says that every number greater than 1 can be represented as the product of two or more prime numbers. That means numbers like 6, 15, all the way up to 100, and beyond can also be written as the product of prime numbers.

So how do we represent numbers using prime factorisation, and is there only one way to do it? Let’s find out!

Unlock unlimited maths questions

Put your learning into practice with fun exercises + games that are proven to boost ability!

Prime factorisation

Factors and prime numbers

In order to understand prime factorisation, we need to understand two very important math terms: prime numbers & factors. Let’s review what those words mean together.

Factors are the numbers you multiply to get an answer.

For example, the factors of the number 5 are 1 and 5.

Prime numbers are any numbers that only have two factors. A good indicator that a number is prime, is if the only factors you can find are the number 1 and itself.

The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, and, 23.

We’re going to keep these numbers handy to use later on in our practice of prime factorisation.

Now let’s combine those two terms to understand the meaning of prime factorisation. What is prime factorisation?

What is prime factorisation?

Prime factorisation is a method used to break down a number using only prime numbers. When you use only prime numbers as factors they are called prime factors.

For example, the prime factors of 15 are 3 and 5, because they are both prime numbers.

Prime factors of a number

How to find the prime factors of a number? Use the list of prime numbers to make prime factorisation easy for you!

Prime number list: 2, 3, 5, 7, 11, 13, 17, 19, and, 23.

For example, what is the prime factorisation of 12? If you look at the list of prime numbers, what combination of prime factors can you multiply to get 12?

____ x _____ x _____ = 12

Think to yourself: “3 x 2 equals 6. So now I’m halfway to 12. If I multiply it by another 2, I will end up with exactly 12.”

So, the prime factors of 12 are 2 x 2 x 3.

Rules when using prime factorisation

Remember, when finding the prime factorisation of a number, it is okay to use the same factor more than once! Just make sure to put the numbers in order from least to greatest as your answer!

So when factoring the number 20 using prime factors, you may find 2 x 5 x 2. But when you put them in order from least to greatest you would write:

2 x 2 x 5 as the prime factorisation of 20.

Explore prime factorisation with DoodleMaths

Meet DoodleMaths, the award-wining maths app that’s proven to double a child’s rate of progression with just 10 minutes of use a day!

Filled with fun, interactive questions covering the whole curriculum, it creates each child a unique work programme tailored to their needs, boosting their confidence and skills in the subject. Try it for free today!

Create a free Doodle account

Prime factorisation methods

There are two main methods to find the prime factorisation of a number. You can use the Factor Tree Method or the Division Method.

1. Factor tree method

The Factor Tree method of prime factorisation starts with a large number and breaks it down until we reach the prime factors. Why is it called a Factor tree? Because all the numbers are connected with lines that look like the branches of a tree.

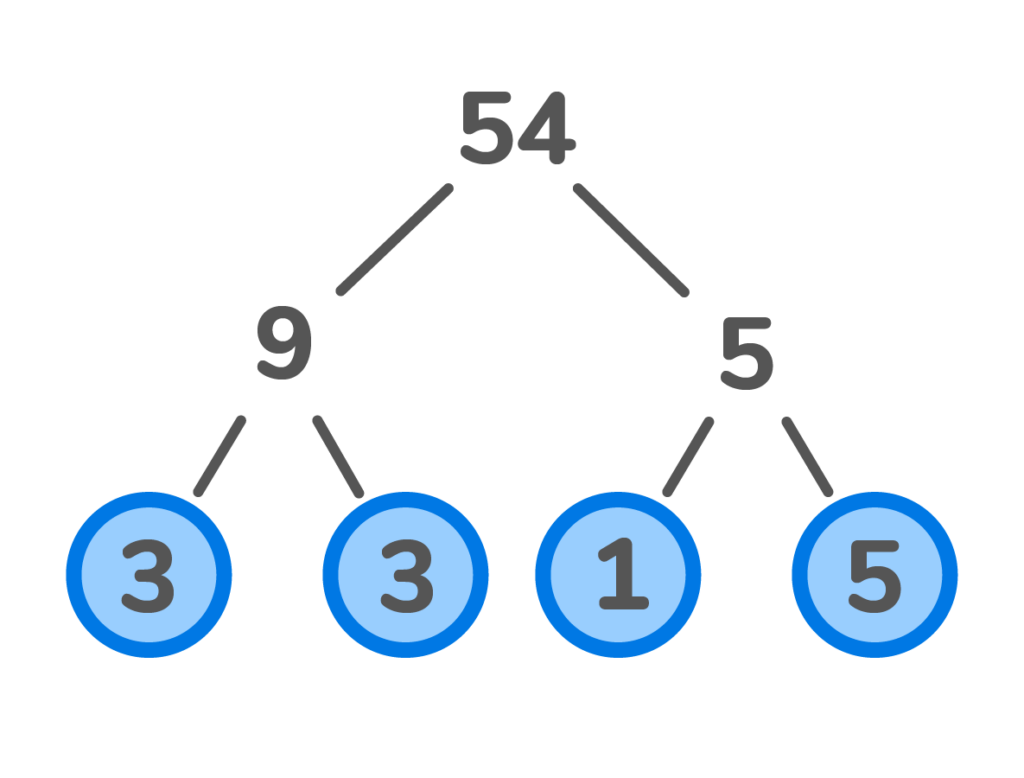
What is the prime factorisation of 54?

First, find two factors that multiply to get 54.

9 x 5
Then, find two factors that multiply to get 9.
3 x 3
Next, find two factors that multiply to get 5.

1 x 5

Once all the factors are prime, you have found all the prime factors.

So, 3 x 3 x 1 x 5 = 54 is the prime factorisation of 54.

2. Division method

The Division Method uses the prime number list to guess and check which numbers can be divided into the number we are trying to factor. Let’s see how to use the Division Method of prime factorisation.

What is the prime factorisation of 49?

First, make a list of prime numbers.

2, 3, 5, 7, 11, 13, 17, 19, 23.

Next, start the process of guessing and checking to see which prime numbers can be divided into 49.

Can 49 be divided by the first prime number 2? No.
Can 49 be divided by the next prime number 3? No.
Can 49 be divided by the third prime number 5? No.
Can 49 be divided by the fourth prime number 7? Yes!

49 divided by 7 is 7. Because 7 and 7 are two prime factors, 7 x 7 is the prime factorisation of 49.

Prime factorisation in real-life scenarios

You may be asking yourself, when do we use prime factorisation in real life? Did you know there are many common examples where we use prime factorisation, including when we are counting money in coins instead of dollars and also when we bake?

For example, if your cake recipe calls for 6 cups of flour. You may find it easier to count measuring 2 cups at a time. You would end up putting in 2 cups 3 different times. 2 x 3 is the prime factorisation of 6.

Prime factorisation practice questions

What is the prime factorisation of 36 using the factor tree method?

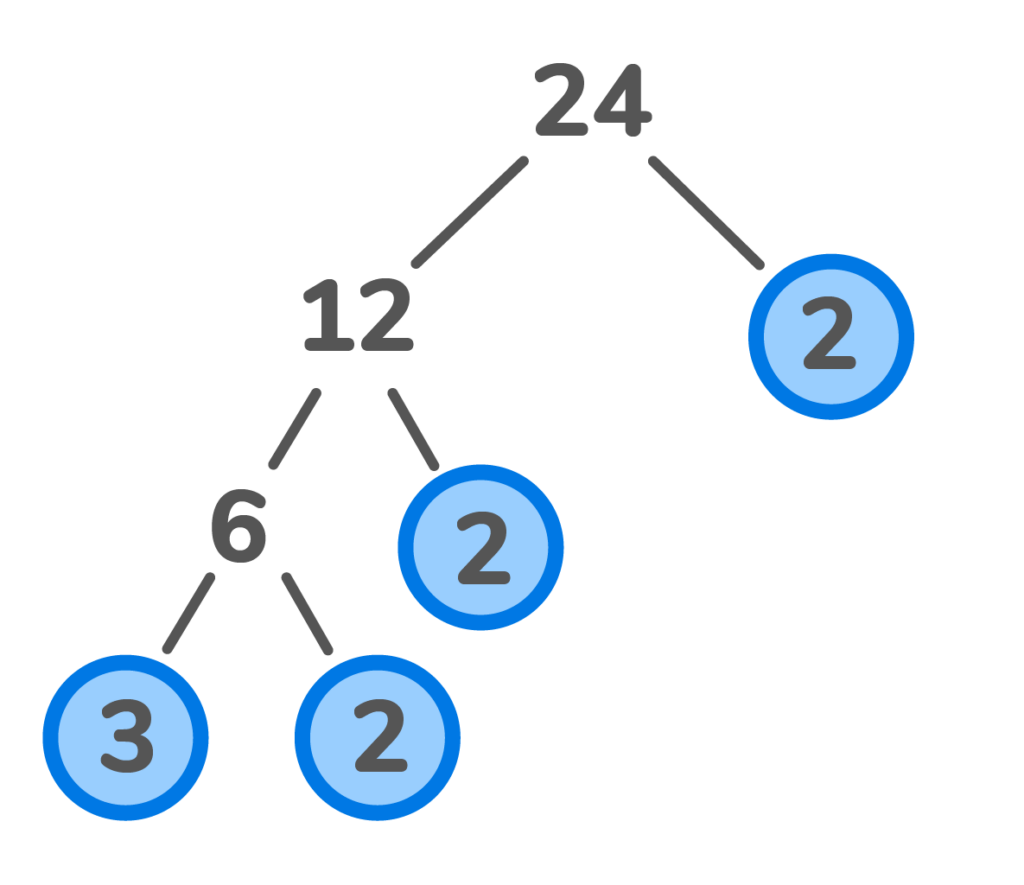
What is the prime factorisation of 24 using the factor tree method?

What is the prime factorisation of 48 using the division method?

What is the prime factorisation of 22 using the division method?

Answers

What is the prime factorisation of 36 using the factor tree method?

1. Write the number 36 on top of the factor tree.
2. Underneath 36, find two numbers that multiply to equal 36, use 12 x 3. Circle the number 3 because it is a prime factor.
3. Since the number 12 is not a prime number, we find two numbers that multiply to equal 12, 4 x 3. Circle the number 3 because it is a prime factor.
4. Since the number 4 is not a prime number, we find two numbers that multiply to equal 4, 2 x 2. Circle both 2’s because they are prime factors.
5. Order the prime factors that were circled from least to greatest 2 x 2 x 3 x 3, which is the prime factorisation of 36.

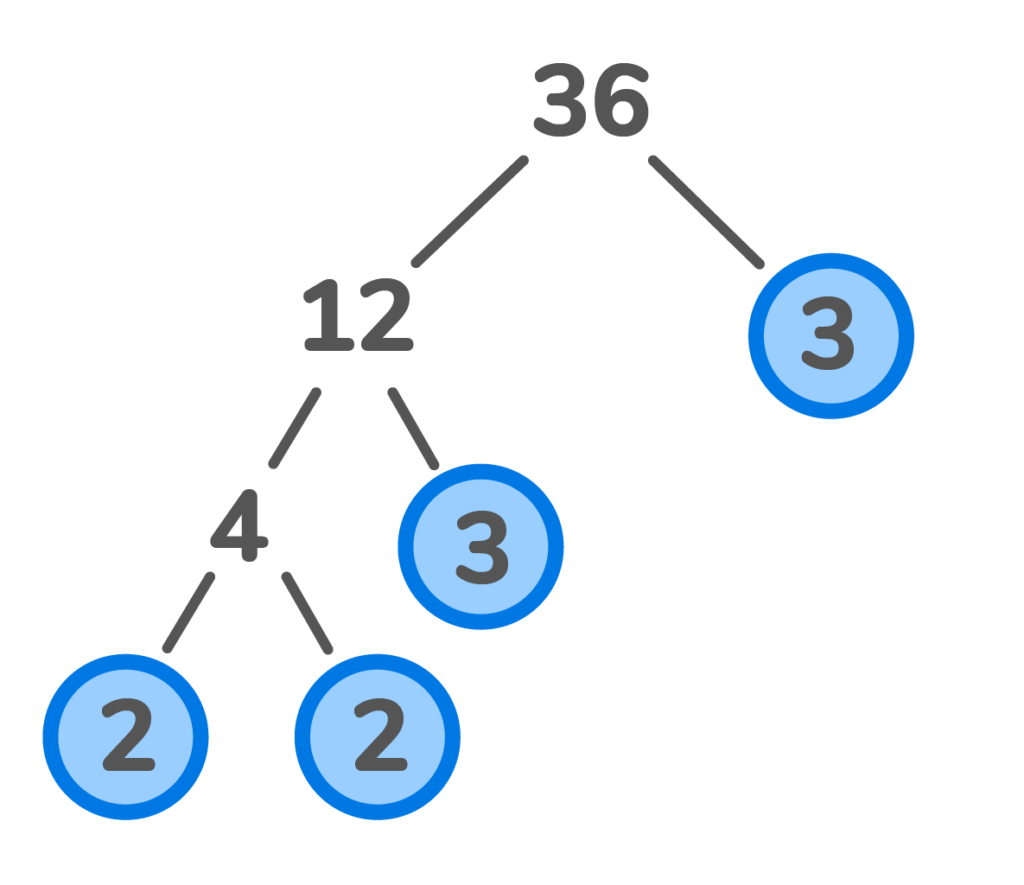
2. What is the prime factorisation of 24 using the factor tree method?

1. Write the number 25 on top of the factor tree.
2. Underneath the 24, find two numbers that multiply to equal 24, 12 x 2. Circle the 2 because it is a prime factor.
3. Since the number 12 is not a prime number, we find two numbers that multiply to equal 12, 6 x 2. Circle the number 2 because it is a prime factor.
4. Since the number 6 is not a prime number, we find two numbers to that multiply to equal 6, 3 x 2. Since they are both prime factors, we circle them both.
5. Order the prime factors that were circled from least to greatest 2 x 2 x 2 x 3, which is the prime factorisation of 24.

3. What is the prime factorisation of 48 using the division method?

1. Write a list of prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23.
2. Begin the process of guess and check:

1. 1. Can 48 be divided by the first prime number 2? Yes. 48 divided by 2 is 24. Circle the number 2 because it is a prime factor.
  2. Can the number 24 be divided by 2? Yes, 24 divided by 2 is 12. Circle the number 2 because it is a prime factor.
  3. Can the number 12 be divided by 2? Yes, 12 divided by 2 is 6. Circle the number 2 because it is a prime factor.
  4. Can the number 6 be divided by 2? Yes, 6 divided by 2 is 3. Circle the 2 and 3 because they are both prime factors.
  5. Now order all the prime factors that were circled from least to greatest: 2 x 2 x 2 x 2 x 3 is the prime factorisation of 48.

4. What is the prime factorisation of 22 using the division method?

1. Write a list of prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23.
2. Begin the process of Guess & Check:
  1. Can 22 be divided by the first prime number 2? Yes, 22 divided by 2 is 11. Because 2 and 11 are prime factors, circle both of them.
  2. Order the factors that were circled from least to greatest: 2 x 11 is the prime factorisation of 22.

FAQs about prime factorisation

What is prime factorisation?

Prime factorisation is when you break down a composite number using only its prime factors.

What are the prime factors of a number?

The prime factors of a number are prime numbers you can multiply to get a number. Prime factors can only be prime numbers.

Why is prime factorisation important?

Prime factorisation is important because one of the most important math theorems relies on it. This theorem states every number greater than 1 can be represented as the product of two or more prime numbers.

When do you use prime factorisation?

You use prime factorisation in fourth and fifth grade, but also in everyday life. For example, you use prime factorisation when counting money in coins instead of dollars. You also use prime factorisation when baking with smaller measurements to add up to the total amount the recipe calls for.