

Learn about the three-dimensional shapes that make up our world.

Author
Tess Loucka
Updated
April 2024


Learn about the three-dimensional shapes that make up our world.

Author
Tess Loucka
Updated
April 2024

Learn about the three-dimensional shapes that make up our world.

Author
Tess Loucka
Updated
April 2024

Key takeaways
Our world is made up of 3D shapes. In fact, our world itself is three-dimensional. Things can move up/down, left/right, and forward/backward.
Our phones, classrooms, houses, and vehicles are all 3D shapes. Even the human body is a 3D shape! Three-dimensional shapes are everywhere we look.
Understanding the three dimensions is essential for geometry, as well as for construction, architecture, athletics, design, and the various fields of science. In the same way that the foundation of a house is made of three-dimensional shapes, a solid foundation of mathematics and even life itself is an understanding of three-dimensional shapes and their properties.
Just like how things in our three-dimensional world can move forward and backward, left and right, and up and down, three-dimensional shapes have three dimensions: length, width, and height.
Those are the three dimensions of our world, and although Einstein claimed that time is a fourth dimension, scientists most commonly explain that life is three-dimensional.
In more detail, 3D shapes are shapes that exist on three planes. They have multiple sides and can be filled in. For example, think of a cereal box.
A cereal box has a length, width, and height, and can be filled in with cereal.
In contrast, 2D shapes exist on a single plane. They have the two dimensions of length and width, but they have no thickness.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Try DoodleMaths for free!
Select a year group
Understanding 3D shapes means understanding their properties. The properties of 3D shapes are as follows:
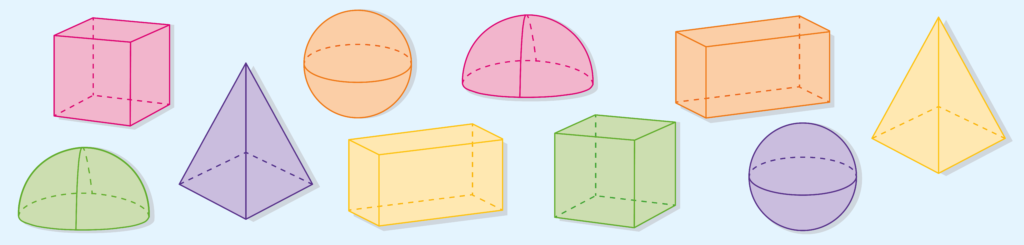
The face of a 3D shape is the flat plane or panel that makes up a side and is bordered by the shape’s edges.
For example, the cube below has six faces: two square faces on the top and bottom, and four around the side.
Most 3D shapes have three or more faces, but not all.
A curved surface doesn’t have any edges, but it is still called a face. So, a cone has two faces, and a sphere has just one.
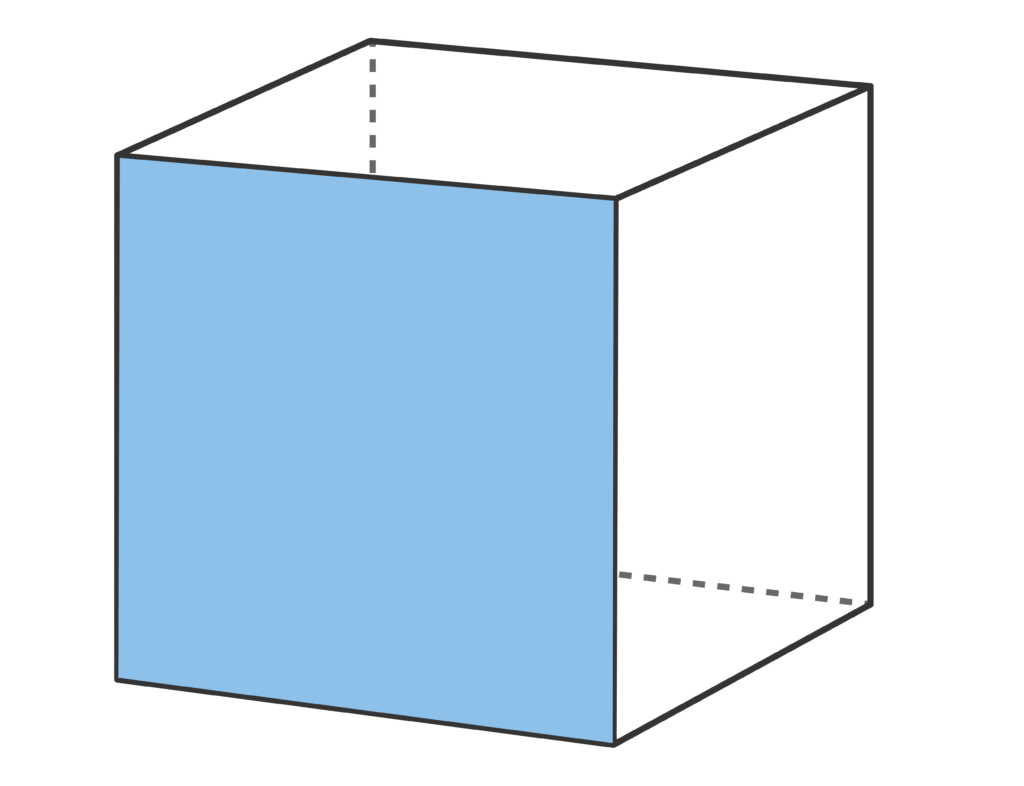
Edges are found on the outside of a face. They mark where one face meets another.
Let’s look at the example of a cube again.
A cube has six square faces. Since a square has four sides, we can say that the top and bottom faces, for instance, each have four edges.
Then, there are an additional four edges around the side of the cube; as such, the total number of edges on a cube is twelve.
On the other hand, cylinders only have two edges: one edge where each circular base meets the rounded body of the cylinder. Cones have one edge since they only have a single circular face joining a curved face.
All 3D shapes have at least one edge. However, there is one exception.
The exception to this rule is spheres. They do not have any edges (since there is only one face and no other faces to join).
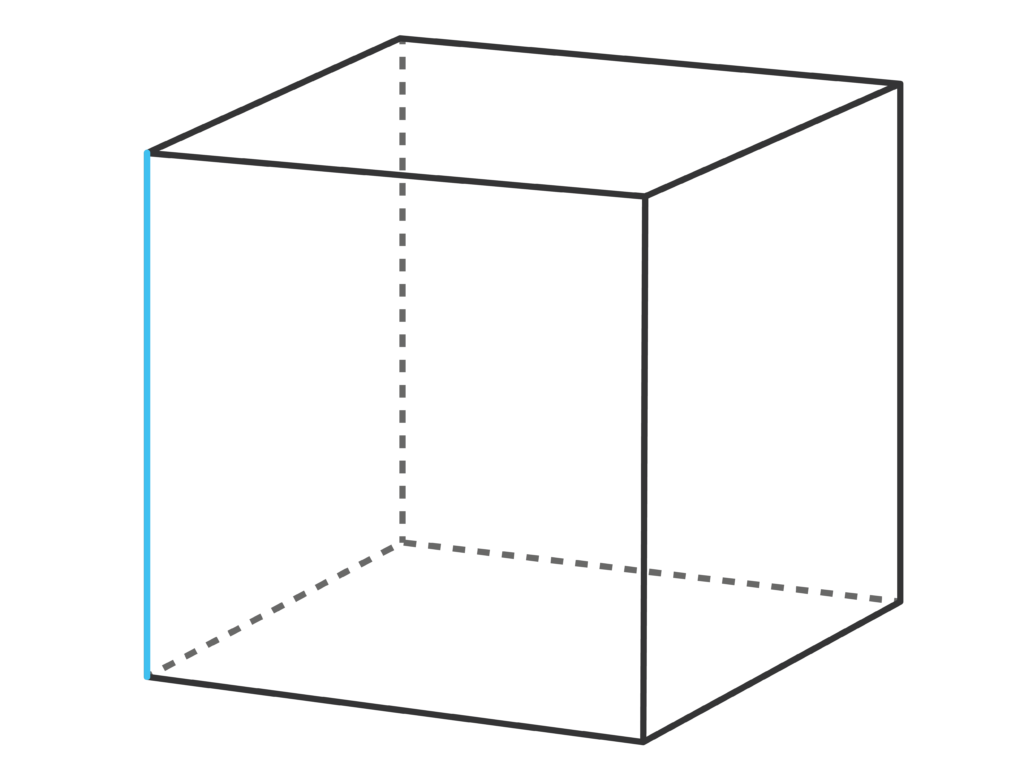
Vertices are the points on the shape where two edges meet. Each of the pointed corners on a cereal box, for example, would be a vertex.
The cube above has eight vertices because there are eight points at which two edges meet.
All 3D shapes have vertices, except for spheres, hemispheres, and cylinders, as these shapes have no points.
All 3D shapes have volume. Volume measures the “fill” of a shape – in other words, how much space the shape can hold inside.
Consider your favorite can of soda. A can is an example of a cylinder, meaning it is a 3D shape and therefore has volume. The average volume of a soda can is 355 milliliters (ml).
When measuring volume, make sure you are either using fluid units, such as fluid ounces or liters, or cubic units such as inches cubed (in3) or centimeters cubed (cm3).
DoodleMaths is an award-winning app that’s filled with thousands of questions and games exploring multiplication, division and more!
Designed by teachers, it creates each child a unique work programme tailored to their needs, doubling their progression with just 10 minutes of use a day.* Try it for free!

*Based on earning 24 stars a day in DoodleMaths. Read full study

Since every object in the world around us exists in three dimensions, there is an endless variety of 3D shapes. However, there are five common three-dimensional shapes that everyone should be familiar with, along with their 2D and 3D names. Let’s go over them using their 3D shape names!
A cube is a 3D shape with 6 square faces, 12 edges, and 8 vertices. A cube is the 3D version of a 2D square.
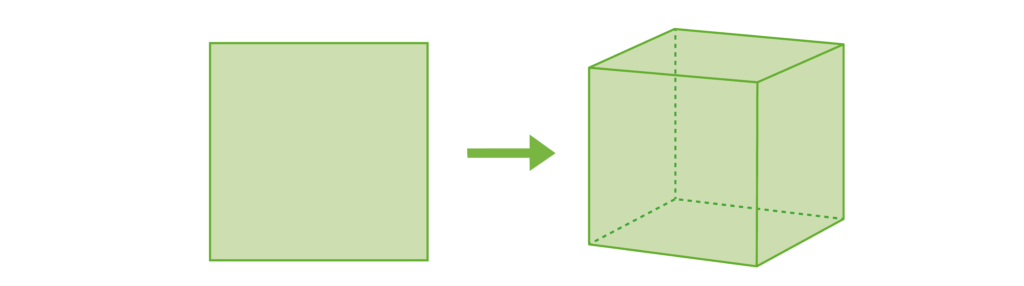
A cuboid is a 3D shape with 6 faces, 12 edges, and 8 vertices. A cuboid is the 3D version of a 2D rectangle.
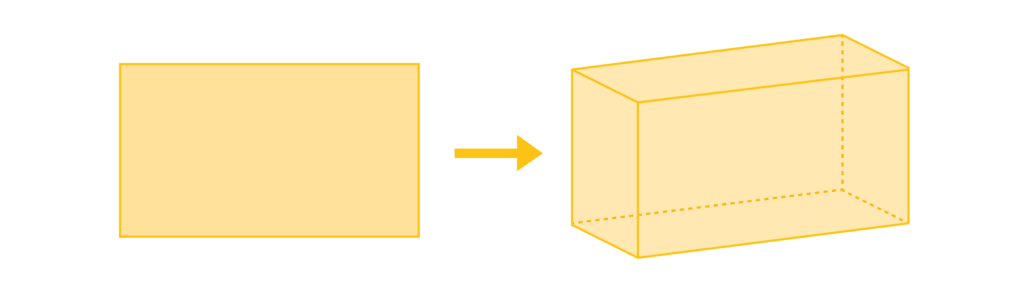
A sphere is a 3D shape that is perfectly round. It has 1 face, 0 edges, and 0 vertices. A sphere is the 3D version of a 2D circle.
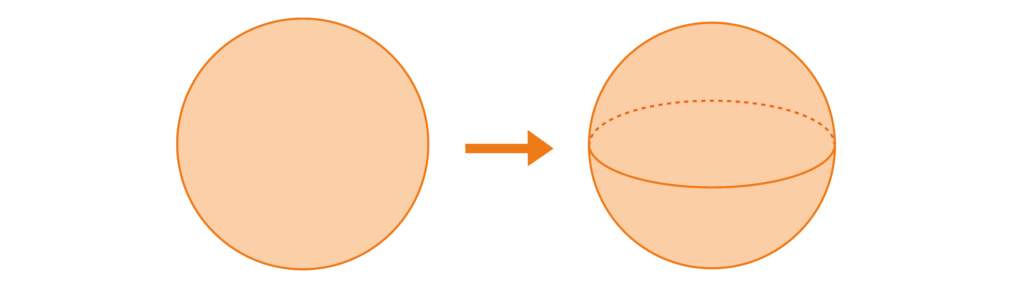
A hemisphere is a 3D shape that is flat on one side and perfectly round on the other. It has 2 faces, only 1 edge, and no vertices. A hemisphere is the 3D version of a 2D semicircle.
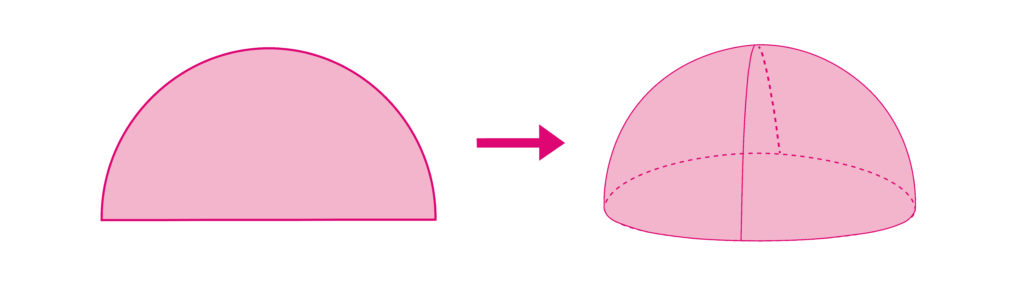
A pyramid is a 3D shape with a flat base and sides that raise to a single point. The 3D pyramid type is dependent on the shape of its base. The shape of the base affects the count of the shape’s faces, edges, and vertices.

Students will not only be expected to identify 3D shapes but must also be able to understand them from the inside out, creating them, and measuring them. Let’s go over the most important measurements to know when dealing with 3D shapes.
The volume of 3D geometric shapes is the area of space they can hold within themselves. Each shape has its own formula for finding volume. Once you know these formulas, finding volume is easy!
The most common volume calculations:
The surface area of 3D geometric shapes is the total area of each of their faces.
To find the surface area of a 3D shape, simply calculate the area of each face and then add the numbers together.

Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: