Learn all about this four-sided polygon and the different shapes it comes in.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: June 2024


Learn all about this four-sided polygon and the different shapes it comes in.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: June 2024




Learn all about this four-sided polygon and the different shapes it comes in.

Author
Taylor Hartley

Expert Reviewer
Jill Padfield
Published: June 2024


Key takeaways
A quadrilateral is a polygon that has four sides, four angles, and four vertices. An easy way to remember this is to think of the word “quad” in quadrilateral which means “four.” If you’re having trouble remembering what “quad” stands for, just think of a motorised quad that has four tires!
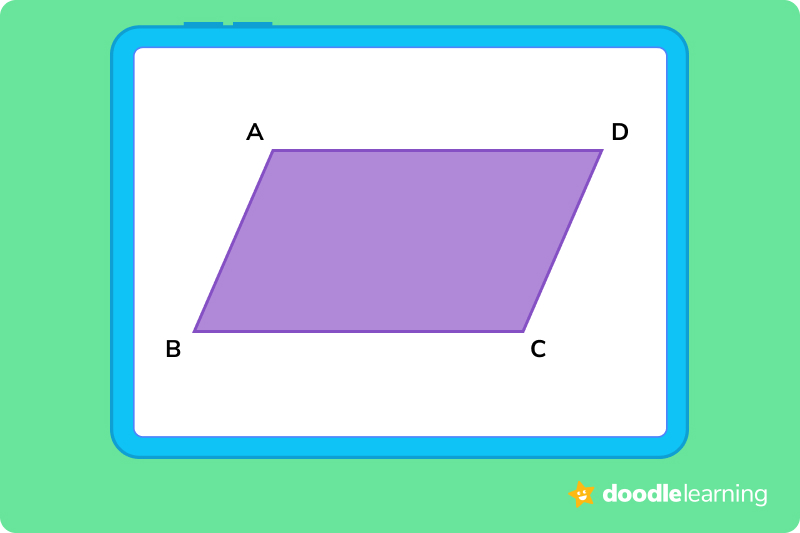
Here is an example of a quadrilateral:

Check out each part of a quadrilateral, and reference the shape above to visualise the components:
Now that you know what a quadrilateral is and what its properties are, let’s take a look at some real-world examples:

Keep in mind, any shape that does not have four sides or four angles, or has open sides is not a quadrilateral.
Unlock unlimited maths questions
Put your learning into practice with fun exercises + games that are proven to boost ability!
Try DoodleMaths for free!
Select a year group
Before we dive into the different types of quadrilaterals, let’s go over a quick list of the common quadrilateral properties — these will be important to remember throughout the practice problems below!
Properties of quadrilateral shapes:
The quadrilateral example that you saw above is only one example out of several. Remember, as long as a shape meets all of the qualifications, it can be a quadrilateral! Here are the different types of quadrilaterals — parallelograms, squares, rectangles, and rhombuses — with picture examples and properties for each.
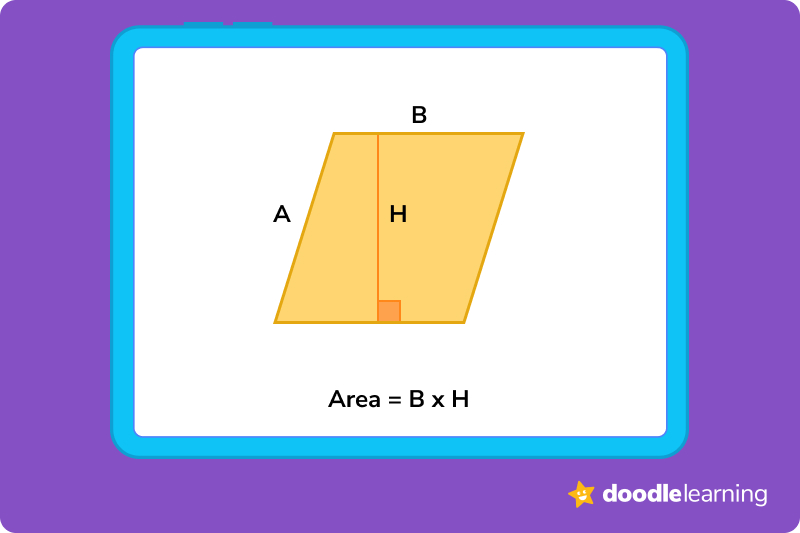
A parallelogram has opposite sides that are parallel and equal, meaning that its opposite sides are two lines in the same plane that are equal distance from each other and never meet and they measure the same length. Its opposite angles are equal, too. Squares, rectangles, and rhombuses are also parallelograms.

A rectangle has opposite sides that are parallel and equal, like the parallelogram. And all angles are equal and measure 90°.

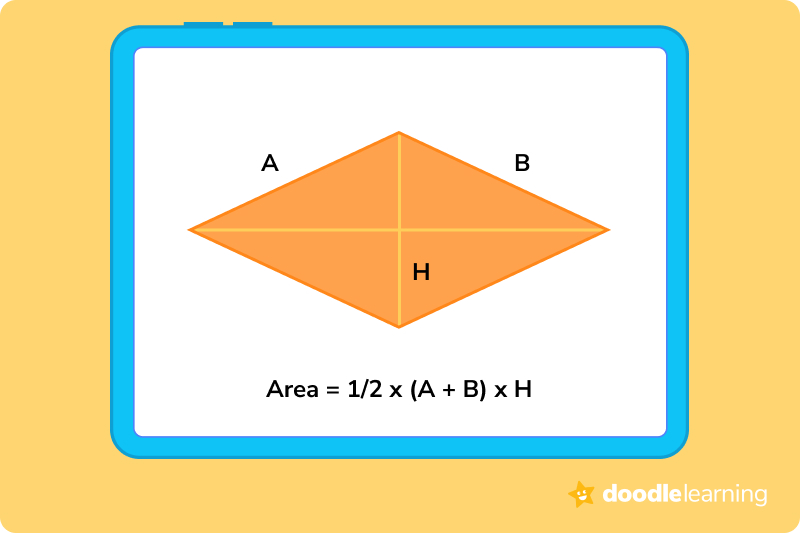
A rhombus is a shape that has all equal sides, and its opposite angles are equal. You might find that definition similar to a square, and it is! But, the difference between a square and a rhombus is that all angles of a square are right angles, but the angles of a rhombus do not have to be right angles. Therefore, every square is a rhombus, but all rhombuses are not squares.

A square is a shape that has all equal sides and angles, and all angles measure 90°.

A trapezium has one pair of opposite sides that are parallel, and its adjacent angles between the non-parallel sides add up to 180°.

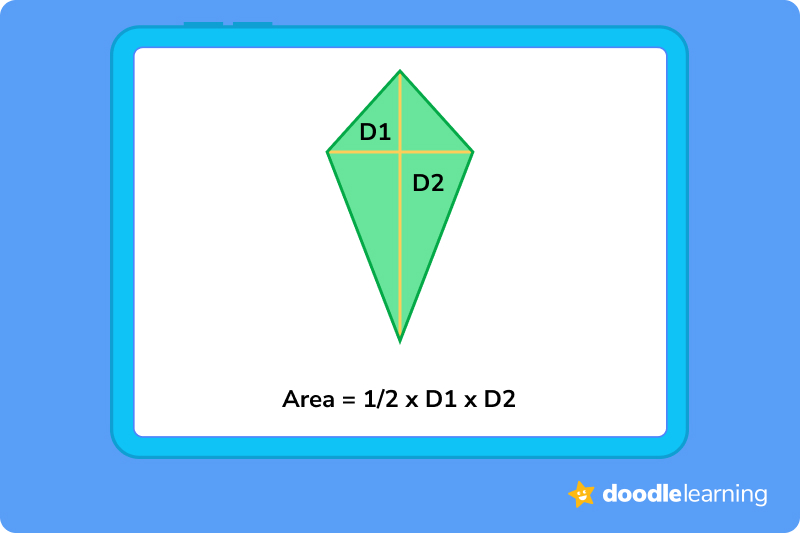
A kite is a shape, too! It has equal adjacent sides, and one pair of opposite angles are equal.

Meet DoodleMaths, the award-wining maths app that’s proven to double a child’s rate of progression with just 10 minutes of use a day!
Filled with fun, interactive questions covering the whole curriculum, it creates each child a unique work programme tailored to their needs, boosting their confidence and skills in the subject. Try it for free today!


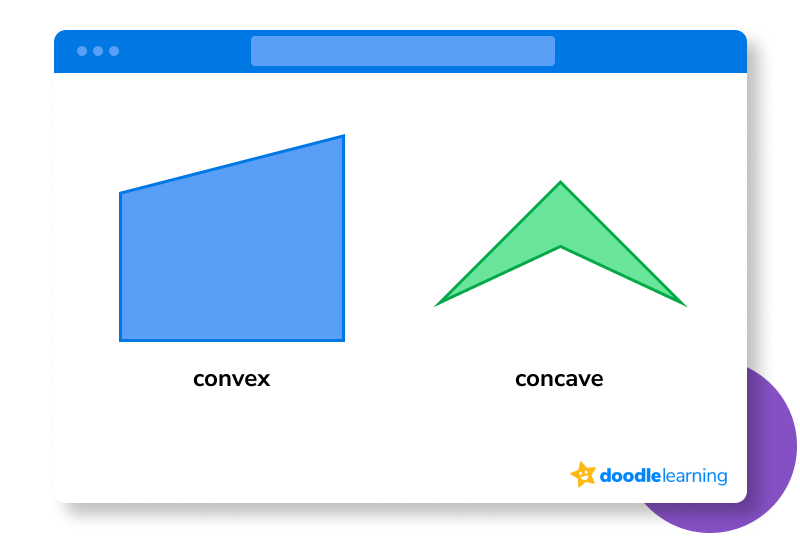
Next, let’s establish the difference between convex and concave quadrilaterals.
Here’s an example of each:
Once you can recognise a quadrilateral and name its properties, you might be asked to find its perimeter and area — so let’s find out how!
The perimeter of a quadrilateral is simply the length of its boundary. In other words, it’s the sum of all of its sides. If ABCD is a quadrilateral, then its perimeter can be expressed as ABCD = AB + BC + CD + DA.
Take a look at some of the different equations you can use to find the perimeter for various types of quadrilaterals:
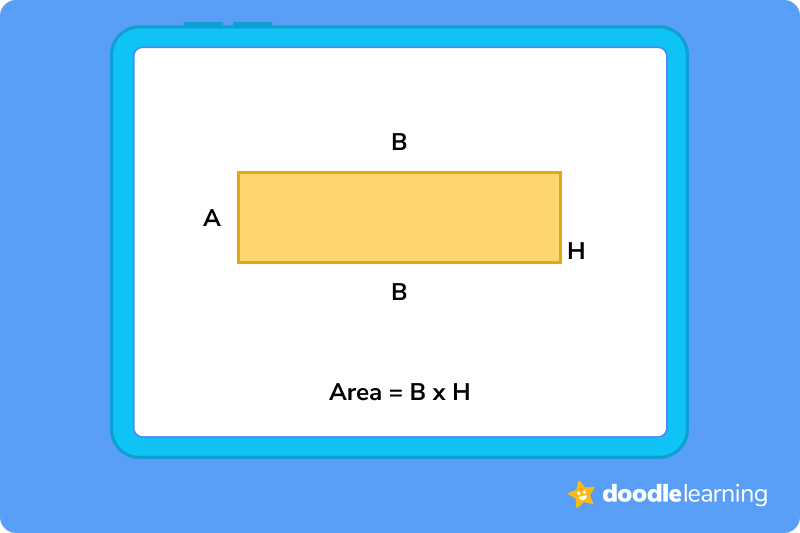
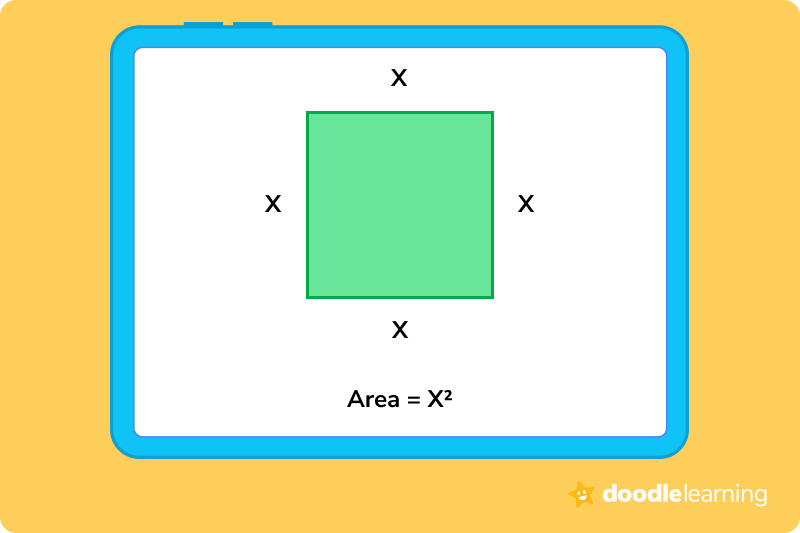
The area of a quadrilateral is just the measurement of the region that’s enclosed by its sides. There are different formulas you have to use for each type of quadrilateral:
Rectangle — b x h
Square — x2
Trapezoid — b x h
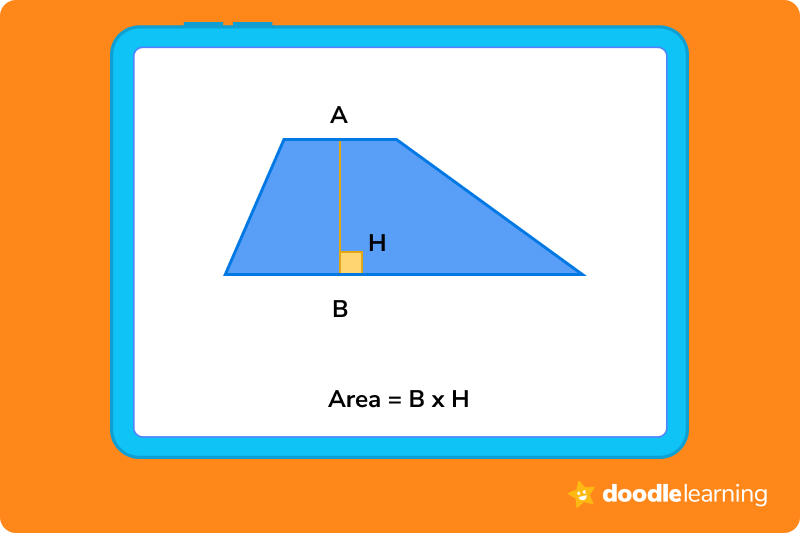
Parallelogram — b x h
Kite — ½ x d1 x d2
Rhombus — ½ x (a + b) x h
1. Find the missing angle ∠C in the following quadrilateral: ∠A = 72° ∠B = 53°, ∠D = 61°
First, it might be helpful for you to draw a quadrilateral and label four angles with the measurements in the problem. One angle, ∠C, will equal x since that is the measurement we’re trying to find.
We know that all the angles of a quadrilateral must equal 360°. So we can add up all of the angles that we do know. 72 + 53 + 61 = 186.
Now, let’s subtract 186 from 360 to find the missing angle ∠C. 360 – 186 = 174.
∠C = 174°
2. What is the perimeter of a quadrilateral with the following side lengths: 10 cm, 6cm, 14cm, and 8cm?
We know that the perimeter of a quadrilateral is just the sum of all of its sides. Therefore, we can add 10 + 6 + 14 + 8 to get 38. The perimeter of this quadrilateral is 38cm.
First, let’s find the equation for the area of a parallelogram which is b x h. We know that the base is 16 cm and the height is 12 cm, so we can rewrite the equation as 16 x 12 = 192. So, the area of this parallelogram is 192 cm2.
Ready to give it a go?
Now that we know the definition of a quadrilateral, the properties of a quadrilateral, and the different types of quadrilaterals, it’s time to put our new skills to the test! Work through the following problems on your own. Feel free to look back at the practice problems above if you get stuck or if you need a quick reminder on what a quadrilateral is.
And remember, don’t get discouraged if you run into a roadblock! Practice is the best way to learn something new.
Click to reveal the answer.
The perimeter is 32 cm.
The answer is true.
The answer is 84 cm2.
It’s a rectangle.
How did we get here?
We know that a rectangle is a type of quadrilateral, and its four angles all measure 90°. Plus, each and both the pair of opposite sides are equal. You could also say this could be a square, since it follows those same properties.
The perimeter is 32 cm.
How did we get here?
True.
How did we get here?
84 cm2
How did we get here?
8 units
How did we get here?
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
There are six main types of quadrilaterals including parallelograms, squares, rectangles, rhombuses, trapezoids, and kites.
A quadrilateral has four vertices and sides, and the sum of all interior angles is 360°. They also have two diagonals.
No, all of the angles cannot be acute because then the sum of angles would be less than 360°.

Lesson credits

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching maths. She's currently working as a Business Analyst and is earning a masters degree in Business Administration.

Taylor Hartley
Taylor Hartley is an author and an English teacher. When she's not writing, you can find her on the rowing machine or lost in a good novel.

Jill Padfield
Jill Padfield has 7 years of experience teaching maths. She's currently working as a Business Analyst and is earning a masters degree in Business Administration.

Parents, sign up for a DoodleMaths subscription and see your child become a maths wizard!

Book a chat with our team
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here: